مرتبسازی کلوچهای
مرتبسازی کلوچهای(به انگلیسی: Pancake sorting) از انواع روشهای مرتبسازی است که در آن معکوس کردن عضوهای بعضی از پیشوندهای یک دنباله تنها کار قابل اجرا میباشد. بر خلاف روشهای سنتی که تلاش میکردند مرتبسازی را با کمترین تعداد مقایسه انجام دهند، در این رویه هدف مرتب کردن دنباله با کمترین تعداد ممکن معکوسسازی است. این عمل را میتوان همانند پشتهای از کلوچهها در نظر گرفت؛ که میتوانیم k کلوچهٔ اول را برداریم و به آن ضربه بزنیم. نوع دیگر مسئله با کلوچههای سوخته سروکار دارد؛ که یک طرف هر کلوچهٔ سوختهاست. در نهایت با رو قرار گرفتن سرِ سوختهٔ کلوچهها پایان میپذیرد.
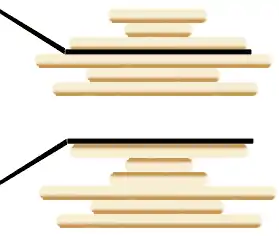
مسئلههای کلوچهای
مسئله اصلی
حداکثر تعداد تلنگر (واژگون سازی) مورد نیاز برای مرتبسازی هر پشته شامل n کلوچه مقداری بین 15/14n و 18/11n نشان داده شدهاست، اما مقدار دقیق آن به دست نیامدهاست.[1]
سادهترین الگوریتم مرتبسازی کلوچهای حداکثر نیاز به 2n−۳ تلنگر دارد. در این الگوریتم، یک نوع مرتبسازی انتخابی، بزرگترین کلوچهٔ مرتب نشده را روی پشته با یک تلنگر (واژگون سازی) قرار میدهیم؛ و سپس با یک تلنگر (واژگون سازی) دیگر آن را به مکان نهایی منتقل میکنیم؛ و این فرایند را برای کلوچههای باقیمانده نیز تکرار میکنیم. به این نکته باید توجه کرد که زمان صرف شده برای پیدا کردن کلوچهها در نظر گرفته نمیشود. تنها عامل مهم تعداد تلنگرها (واژگون سازی) ست. به منظور پیادهسازی ماشینی که بتواند این رویه را در زمان خطی انجام دهد باید واژگونسازی پیشوندها و پیدا کردن بیشینه محدوده ازاعداد متوالی دار دنباله در زمان ثابت اجرا شود. در ۱۷ سمپتامبر سال ۲۰۰۸ گروهی از محققان در دانشگاه تگزاس در دالاس به رهبری بنیانگذار هال سودبرو[2] پذیرفته شدن یک روش بهینه تر از آن چیزی که گیتس و پپدیمیتریو برای مراتبسازی کلوچهای ارائه داده بودند را توسط مجلهٔ علوم کامپیوتر نظری اعلام کردند.[3][4] در ۲ نوامبر سال ۲۰۱۱ یک مقاله به ارخیو ارائه شد که اثبات میکرد که مسٔله انپی سخت است، در نتیجه در پاسخ به سؤال باز برای بیش از سه دهه.[1]
مسئله کلوچه سوخته
در یک نوع پیچیدهتر که مرتبسازی کلوچه سوخته نامید میشود که زمانی پایان میپذیرد که طرف سوختهٔ همهٔ کلوچهها روی به پایین قرار گیرد. در سال ۲۰۰۸ گروهی از دانشجویان یک رایانه باکتریایی (bacterial computer) ساختند که میتوانست مسئله سادهٔ مرتبسازی کلوچه سوخته را با استفاده از برنامهنویسی E. coliحل کند.[5][6]
DNA دارای جهت گیرصی و نظم است. با وجود قدرت پردازشی پایین DNA فلیپها. بالا بودن تعداد باکتریها در این روش شالودهٔ گستردهای از محاسبات موازی را فراهم میکند. این باکتری با مقاومت در برابر آنتیبیوتیکها زمان حل مسئله را علم میکند.[7] انیمتینی که این فرایند را به تصویر میکشد ساخته شدهاست.[8]
مسئله کلوچهای بر روی رشتهها
گفتههای بالا نشان میدهد که هر کلوچه منحصر به فرد است. یعنی هیچ دو تایی از آنها یکسان نیستند. از این روی دنبالهای که روی آن معکوسها انجام میشود یک جایگشت است. بهطور مثل یک دنبالهای که هر نمد تنها یک بر تکرار میشود. در حالی که "رشتههاً دنبالههایی هستند که نمدها میتوانند بیش از یک بر در آنها تکرار شوند. چیطوری(Chitturi) و سودبرو (۲۰۱۰) (Sudborough) و هورکنس ات ال. (۲۰۰۷) (.Hurkens et al)جداگانه نشان دادند که پیچیدگی تبدیل یک رشتهٔ سازگار را به رشتهای دیگر با استفاده از وژگونسازی پیشوندها انپی کامل است.
هورکنس ات ال. (.Hurkens et al) الگوریتمی دقیق برای جستجو ددی و رشته ستایی بیان کرد.. چیتوری (۲۰۱۱) (Chitturi)اثبات کرد که پیچیدگی تبدیل یک رشتهٔ سازگار به رشتهای دیگر با استفاده از وژگونسازی پیشوندها، مانند مسئله کلوچهٔ سوخته NP_complete است.
تاریخچه
اگر چه اغلب به عنوان یک وسیله آموزشی دیده میشود، مرتبسازی کلوچهای در برنامههای کاربردی در شبکههای پردازنده موازی نیز دیده میشود، که میتواند الگوریتم مؤثر مسیریابی بین پردازنده فراهم کند.
این مسئله به عنوان تنها مقالهٔ ریاضیات مشهور که تاکنون توسط بنیانگذار مایکروسافت بیل گیتس (به عنوان ویلیام گیتس)، تحت عنوان «مرزهای برای دستهبندی بر اساس واژگونی پیشوند» در سال ۱۹۷۹ منتشر شدهاست، قابل توجهاست؛ که یک الگوریتم کارآمدرا برای مرتبسازی کلوچهای توصیف میکند.[9] علاوه بر این، قابل توجهترین مقاله منتشر شده توسط فوتوراما فوتوراما همکار دیوید کوهن دیوید اکس. کوهن (به عنوان S. دیوید کوهن) در ارتباط با مسئلهٔ کلوچهٔ سوختهاست.[10] همکاران آنها کریستوس پاپادیمیتریو (سپس در دانشگاه هاروارد، در حال حاضر در برکلی) و مانوئل بلومManuel Blum (سپس در برکلی، در حال حاضر در دانشگاه کارنگی ملون دانشگاه کارنگی ملون)، بودند. مشکلات به هم پیوستهٔ مراتبسازی علامتدار با استفاده از وژگونسازی و مراتبسازی با استفاده از وژگونسازی اخیراً بیشتر مورد مطالعه قرار گرفتهاند. در حالی که الگوریتم بهینه برای مراتبسازی با استفاده از وژگونسازی پیدا شدهاست. [Kaplan, Shamir, Tarjan, 1997],[11] اثبات شدهاست که حل مسئله مرتبسازی با واژگونسازی مشکل است حتی بهدست آوردن تقریب آن با استفاده از شاخصهای ثابت.[Berman, Karpinski, 1999],[12] همچنین ثابت میشود که قابل تخمینزنی در زمان چندجملهای است با شاخص تقریبی ۱٫۳۷۵ [Berman, Karpinski, Hannenhalli, 2002].[13]
توالیهای عدد صحیح مرتبط
| ارتفاع | N | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | |
| ۱ | ۱ | ||||||||||||||
| ۲ | ۱ | ۱ | |||||||||||||
| ۳ | ۱ | ۲ | ۲ | ۱ | |||||||||||
| ۴ | ۱ | ۳ | ۶ | ۱۱ | ۳ | ||||||||||
| ۵ | ۱ | ۴ | ۱۲ | ۳۵ | ۴۸ | ۲۰ | |||||||||
| ۶ | ۱ | ۵ | ۲۰ | ۷۹ | ۱۹۹ | ۲۸۱ | ۱۳۳ | ۲ | |||||||
| ۷ | ۱ | ۶ | ۳۰ | ۱۴۹ | ۵۴۳ | ۱۳۵۷ | ۱۹۰۳ | ۱۰۱۶ | ۳۵ | ||||||
| ۸ | ۱ | ۷ | ۴۲ | ۲۵۱ | ۱۱۹۱ | ۴۲۸۱ | ۱۰۵۶۱ | ۱۵۰۱۱ | ۸۵۲۰ | ۴۵۵ | |||||
| ۹ | ۱ | ۸ | ۵۶ | ۳۹۱ | ۲۲۷۸ | ۱۰۶۶۶ | ۳۸۰۱۵ | ۹۳۵۸۵ | ۱۳۲۶۹۷ | ۷۹۳۷۹ | ۵۸۰۴ | ||||
| ۱۰ | ۱ | ۹ | ۷۲ | ۵۷۵ | ۳۹۶۳ | ۲۲۸۲۵ | ۱۰۶۴۶۱ | ۳۷۷۸۶۳ | ۹۱۹۳۶۵ | ۱۳۰۹۷۵۶ | ۸۱۴۶۷۸ | ۷۳۲۳۲ | |||
| ۱۱ | ۱ | ۱۰ | ۹۰ | ۸۰۹ | ۶۴۲۹ | ۴۳۸۹۱ | ۲۵۲۷۳۷ | ۱۱۷۴۷۶۶ | ۴۱۲۶۵۱۵ | ۹۹۸۱۰۷۳ | ۱۴۲۵۰۴۷۱ | ۹۱۲۳۶۴۸ | ۹۵۶۳۵۴ | ۶ | |
| ۱۲ | ۱ | ۱۱ | ۱۱۰ | ۱۰۹۹ | ۹۸۸۳ | ۷۷۹۳۷ | ۵۳۳۳۹۷ | ۳۰۶۴۷۸۸ | ۱۴۱۴۱۹۲۹ | ۴۹۳۳۷۲۵۲ | ۱۱۸۴۲۰۰۴۳ | ۱۶۹۳۳۲۲۱۳ | ۱۱۱۰۵۰۰۶۶ | ۱۳۰۳۲۷۰۴ | ۱۶۷ |
دنبالهها از: The Online Encyclopedia of Integer Sequences of Neil Sloane
پانویس
- Bulteau, L. and Fertin, G. and Rusu, I. Pancake Flipping Is Hard. Submitted, 2011.
- Hal Sudborough
- "Team Bests Young Bill Gates With Improved Answer to So-Called Pancake Problem in Mathematics". University of Texas at Dallas News Center. September 17, 2008. Archived from the original on 5 April 2012. Retrieved 2008-11-10.
A team of UT Dallas computer science students and their faculty adviser have improved upon a longstanding solution to a mathematical conundrum known as the pancake problem. The previous best solution, which stood for almost 30 years, was devised by Bill Gates and one of his Harvard instructors, Christos Papadimitriou, several years before Microsoft was established.
- Chitturi, B. , Fahle, W. , Meng, Z. , Morales, L. , Shields, C.O. , Sudborough, I. H. , and Voit, W. «An (18/11)n upper bound for sorting by prefix reversals." Theoretical Computer Science, 410(36), 3372-3390, 2009.
- «Solving the Pancake Problem with an E. coli Computer». بایگانیشده از اصلی در ۶ آوریل ۲۰۱۲. دریافتشده در ۸ دسامبر ۲۰۱۱.
- «iHOP meets iGEM». بایگانیشده از اصلی در ۹ مارس ۲۰۱۲. دریافتشده در ۸ دسامبر ۲۰۱۱.
- Haynes, K.A. , et al. «Engineering bacteria to solve the Burnt Pancake Problem." Journal of Biological Engineering, 2(1), 8, 2008.
- E.HOP - E. coli House of Pancakes - computing in vivo بایگانیشده در ۱۲ فوریه ۲۰۱۲ توسط Wayback Machine (flash applet)
- Gates, W. and کریستوس پاپادیمیتریو "Bounds for Sorting by Prefix Reversal." بایگانیشده در ۱۰ ژوئن ۲۰۰۷ توسط Wayback Machine Discrete Mathematics, 27, 47-57, 1979.
- دیوید اکس. کوهن and Blum, M. «On the problem of sorting burnt pancakes." Discrete Applied Mathematics, 61, 105-120, 1995.
- Kaplan, H. , Shamir, R. and Tarjan, R.E. "Faster and Simpler Algorithm for Sorting Signed Permutations by Reversals." Proc. 8th ACM-SIAM SODA (1997), 178-187, 1997.
- Berman, P. and Karpinski, M. "On Some Tighter Inapproximability Results." Proc. 26th ICALP (1999), LNCS 1644, Springer, 200-209, 1999.
- Berman, P. , Karpinski M. and Hannenhalli, S. , «1.375-Approximation Algorithms for Sorting by Reversals." Proc. 10th ESA (2002), LNCS 2461, Springer, 200-210, 2002.
برای مطالعهٔ بیشتر
- Mohammad, H.H. and Hal Sudborough, I. "On the Diameter of the Pancake Network," Journal of Algorithms 25 (1), 67-94, 1997.
- Roney-Dougal, C. and Vatter, V. "Of pancakes, mice and men," Plus Magazine 54, March 2010.
- Chitturi, B. and Sudborough, H. "Prefix reversals on strings". Proc. Int. Conf. Bioinformatics and Computational Biology, Vol. 2 (2010)591–598.
- Hurkens, C. , Iersel, L. V. , Keijsper, J. , Kelk, S. , Stougie, L. and Tromp J. "Prefix reversals on binary and ternary strings". SIAM J. Discrete Math. 21(3)(2007) 592–611.
- Chitturi, B. "A note on complexity of genetic mutations". DMAA 3(3) (2011)269-286 doi:10.1142/S1793830911001206.
پیوند به بیرون
- Cut-the-Knot: Flipping pancakes puzzle, including a Java applet for the pancake problem and some discussion.
- Douglas B. West's "The Pancake Problems"
- Weisstein, Eric W. "Pancake Sorting". MathWorld.
- Animation explaining the bacterial computer that can solve the burnt pancake problem.
