بخش‌بندی تصویر

در بینایی رایانه‌ای، بخش‌بندی تصویر، به فرایند قطعه‌بندی کردن یک تصویر دیجیتال به چند بخش (مجموعه از پیکسل‌ها، همچنین با عنوان سوپر پیکسل شناخته می‌شود) گفته می‌شود. هدف بخش‌بندی، ساده‌سازی یا/و تغییر در نمایش یک تصویر به چیزی ست که هم معنی دارتر و هم برای آنالیز آسان‌تر است.[1][2] بخش‌بندی تصویر معمولاً برای پیدا کردن محل اشیا موردنظر و مرزها (خطوط، منحنی‌ها و غیره) در تصویر استفاده می‌شود. به عبارت دقیق‌تر، بخش‌بندی تصویر، به فرایندی گفته می‌شود که در آن، به هر پیکسل، برچسبی اختصاص داده می‌شود، به طوری که پیکسل‌هایی با برچسب یکسان، ویژگی‌های مشابهی دارند.

مدل بخش بندی شده از استخوان ران. این مدل سطح خارجی (قرمز)، سطح بین قسمت چگال و اسفنجی (سبز) و سطح مربوط به مغز استخوان (آبی) را نشان می‌دهد.

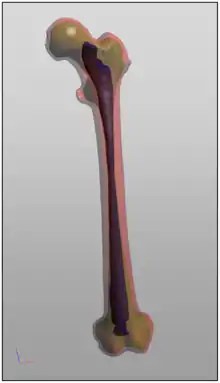
خروجی فرایند بخش بندی تصویر، مجموعه ای از بخش‌هاست که اجتماع آنها، کل تصویر را شامل می‌شود و یا مجموعه ای از خطوط که از تصویر استخراج شده‌اند. هر یک از پیکسل‌ها در هر بخش، از نظر داشتن ویژگی‌های خاص مانند رنگ، شدت روشنایی و یا بافت، شبیه به یکدیگر هستند. بخش‌های مجاور با توجه به ویژگی‌های ذکر شده، نسبت به هم متفاوت محسوب می‌شوند. هنگامی‌که این پردازش‌ها به یک دسته از تصاویر، به خصوص تصاویر پزشکی اعمال می‌شوند، کانتورها یا نقشه‌های برجسته به دست آمده، می‌توانند با کمک الگوریتم‌های درون یابی نظیر Marching cubes برای بازسازی سه بعدی، استفاده شوند.

کاربردها

بخش بندی حجم از یک تصویر سی تی اسکن سه بعدی از قفسه سینه: دیوار قدامی قفسه سینه، راه‌های هوایی و عروق ریوی قدامی به منظور تجسم قفسه سینه، به صورت دیجیتالی حذف شده اند. محتوا:
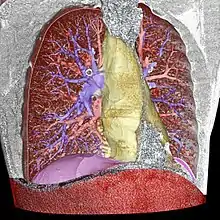
- آبی: سرخرگ ریوی
- قرمز: سیاهرگ ریوی (و همچنین دیواره شکم)
- زرد: mediastinum
- بنفش: دیافراگم

برخی از کاربردهای عملی بخش بندی تصاویر به شرح زیر است:

• بازیابی محتوا محور تصاویر
• بینایی رایانه‌ای
• تصویربرداری پزشکی [3][4] از جمله حجم رندر تصاویر از سی‌تی اسکن و تصویر برداری رزونانس مغناطیسی.
  • تعیین محل تومور و دیگر بیماری‌های[5][6]
  • اندازه‌گیری حجم بافت
  • تشخیص و مطالعه ساختار تشریحی[7]
  • برنامه‌ریزی برای عمل جراحی
  • شبیه سازی جراحی مجازی
  • موقعیت یابی در جراحی
• تشخیص شی[8]
  • تشخیص عابر پیاده
  • تشخیص چهره
  • تشخیص ترمز نور
  • مکان یابی اشیاء در تصاویر ماهواره‌ای (جاده، جنگل، محصولات و غیره.)
• شناخت وظایف
• تشخیص اثر انگشت
• تشخیص عنبیه
• سیستم‌های کنترل ترافیک
• نظارت ویدئویی

تعداد زیادی الگوریتم عمومی و تکنیک، به منظور بخش بندی تصویر، توسعه داده شده‌است. برای کارآمد بودن، این تکنیک‌ها به‌طور معمول باید با دانش خاص ناحیه ترکیب شوند تا بتواند مسائل بخش بندی ناحیه را به‌طور مؤثر حل کنند.

آستانه گذاری

ساده‌ترین روش در بخش‌بندی تصویر، آستانه گذاری نام دارد. این روش بر اساس سطح آستانه، یک عکس خاکستری را به یک عکس باینری تبدیل می‌کند. همچنین یک نوع آستانه گذاری بر اساس هیستوگرام متوازن شده نیز وجود دارد.

نکته کلیدی در این روش، انتخاب مقدار آستانه (یا مقادیر آستانه برای حالتی که چند سطح مورد نظر است.) می‌باشد. چندین روش مشهور نظیر آنتروپی ماکزیمم، واریانس ماکزیمم و خوشه‌بندی کی-میانگین (k-mean) در صنعت مورد استفاده قرار می‌گیرند.

اخیراً روش‌هایی برای آستانه گذاری در تصاویر سی‌تی اسکن توسعه داده شده‌اند. نکته کلیدی در آن‌ها این است که برعکس روش واریانس ماکزیمم، مقادیر آستانه به جای تصویر بازسازی شده، از تصویر رادیوگرافی مشتق می‌شود .[9][10]

روش‌های جدیدی بر اساس استفاده از مقادیر آستانه غیرخطی فازی چندلایه پیشنهاد شده‌است. در این روش‌ها، بر اساس عضویتی که به هر پیکسل اختصاص داده می‌شود و همچنین مفاهیم منطق فازی و الگوریتم فرگشتی، عمل بخش‌بندی را انجام می‌دهند.[11]

روش‌های مبتنی بر خوشه بندی

تصویر اصلی

تصویر پردازش شده با اعمال الگوریتم K-means با k=16. توجه داشته باشید که یک تکنیک مشترک برای بهبود عملکرد الگوریتم در تصاویر بزرگ، کم کردن تعداد نمونه هاست.

الگوریتم خوشه‌بندی کی-میانگین (k-mean) یک تکنیک تکرار شونده می‌باشد که برای قطعه بندی یک تصویر به k قطعه، مورد استفاده قرار می‌گیرد.[12] گام‌های پیاده‌سازی الگوریتم به شرح زیر است:

1. انتخاب k تا مرکز برای خوشه‌ها، یا به صورت تصادفی یا بر اساس روش اکتشافی. برای مثال k-means.
2. اختصاص یک خوشه به هر پیکسل، به طوری که فاصله مرکز خوشه و محل پیکسل مینیمم شود.
3. محاسبه مجدد مرکز خوشه‌ها با محاسبه میانگین تمام پیکسل‌های موجود در خوشه.
4. تکرار مراحل 2 و 3 تا زمانی که همگرایی لازم حاصل شود. (هیچ پیکسلی خوشه‌ها را تغییر ندهد)

در این مسئله، فاصله، جذر یا تفریق مطلق بین محل پیکسل و مرکز خوشه می‌باشد. این تفاوت معمولاً بر اساس رنگ، شدت روشنایی، بافت و موقعیت پیکسل یا ترکیبی وزن‌دار از این فاکتورهاست. عدد k می‌تواند به صورت دستی، تصادفی و یا بر اساس فرایند اکتشافی انتخاب شود. این الگوریتم تضمین می‌کند که همگرایی حاصل می‌شود، اما ممکن است راه حل آن بهینه نباشد. کیفیت راه حل به شرایط اولیه خوشه‌ها و مقدار k بستگی دارد.

حرکت و بخش‌بندی تعاملی

بخش‌بندی مبتنی بر حرکت، تکنیکی ست که بر پایه حرکت شی در تصویر می‌باشد.

ایده اصلی ساده است: به تفاوت‌های یک جفت از تصاویر نگاه کنید. فرض کنید که شی موردنظر در حال حرکت باشد، تفاوت بین دو عکس دقیقاً با ناحیه اشغال شده توسط شی برابر است.

روش kenney با ارائه روش بخش‌بندی تعاملی، این ایده را گسترش داد. آن‌ها از یک ربات برای به حرکت درآوردن اشیاء به منظور تولید سیگنال حرکتی لازم برای بخش‌بندی مبتنی بر حرکت استفاده کردند.

بخس بندی تعاملی، چارچوب درک تعاملی ای که توسط Dov Katz و Oliver Brock ارائه شده‌است را دنبال می‌کند.

روش مبتنی بر فشرده سازی

روش‌های مبتنی بر فشرده‌سازی، فرض می‌کند که بخش‌بندی بهینه از بین تمامی روش‌های ممکن، کمترین مقدار طول دیتا را دارد[13][14] ارتباط این دو مفهوم این است که بخش‌بندی سعی می‌کند تا الگوها یا هر نظم و قاعده دیگری را پیدا کند که بتوان از آن برای کم کردن حجم دیتا استفاده کرد. این روش هر بخش را با بافت و شکل مرز آن توصیف می‌کند. هر یک ازین اجزا توسط یک تابع توزیع احتمال مدل می‌شود. محاسبه طول کد مربوط به آن در ادامه توضیح داده می‌شود:

1. رمز گذاری مرز، این واقعیت را بیان می‌دارد که بخش‌ها در تصاویر طبیعی تمایل به داشتن مرزهای نرم دارند. این مفهوم توسط کدگذاری هافمن برای کد کردن یک زنجیره کد از مرزها در تصویر استفاده شده‌است؛ بنابراین هرچه مرزهای یک بخش نرم‌تر باشند، کد گذاری آن طول کمتری را اشغال می‌کند
2. بافت ناحیه‌ها، توسط روش فشرده‌سازی با اتلاف بر اساس اصول روش minimum description length، کد گذاری می‌شوند. اما در اینجا، طول دیتا با تعداد نمونه‌ها در آنتروپی مدل تخمین زده می‌شود. بافت هر ناحیه از تصویر، با روش multivariate normal distribution تخمین زده می‌شود که ضابطه آنتروپی آن دارای یک فرم بسته‌است. یک ویژگی جالب این مدل آن است که آنتروپی تخمین زده شده به آنتروپی واقعی بسیار نزدیک است. دلیل این اتفاق این است که در بین تمامی توزیع‌های آماری با میانگین و کوواریانس مشخص، توزیع نرمال بیشترین مقدار آنتروپی را داراست؛ بنابراین طول کد نمی‌تواند بیشتر از مقداری باشد که الگوریتم در حال مینیمم کردن آن است.

برای هر بخش در یک تصویر، این طرح تعداد بیت‌های مورد نیاز برای کدکردن یک تصویر بر اساس بخش‌های داده شده را، تولید می‌کند؛ بنابراین در بین تمامی بخش‌بندی‌های ممکن، هدف پیدا کردن بخش‌بندی‌ای است که کوتاه‌ترین طول کُد ممکن را تولید کند. این کد به سادگی می‌تواند توسط روش خوشه بندی agglomerative حاصل شود. اعوجاج در روش فشرده سازی با اتلاف حاکی از برابری بخش‌بندی‌ها دارد و مقدار بهینه آن می‌تواند برای عکس‌های مختلف، از یکدیگر متفاوت باشد. این پارامتر می‌تواند از روی کانترست بافت‌ها در تصویر حاصل شود. برای مثال وقتی کانترست بافت‌ها در تصویر یکسان است، مانند تصاویر camouflage، خروجی از حساسیت بیشتری برخوردار است و کوانتیزه شدگی کمتری دارد.

روش‌های مبتنی بر هیستوگرام

روش‌های مبتنی بر هیستوگرام نسبت به سایر روش‌های بخش‌بندی بسیار کارآمد هستند. دلیل این امر آن است که این روش‌ها تنها به یکبار وارسی پیکسل‌ها نیاز دارند. در این روش هیستوگرام از روی تمامی پیکسل‌های موجود در تصویر محاسبه می‌شود و قله‌ها و دره‌های موجود در منحنی هیستوگرام برای پیدا کردن مکان کلاس‌ها، مورد استفاده قرار می‌گیرند. در این تکنیک، رنگ یا شدت نور می‌تواند به عنوان یک معیار سنجش لحاظ شود.

ورژن اصلاح شده این تکنیک، اعمال روش جستجوگر هیستوگرام برای تقسیم یک تصویر به کلاس‌های کوچک‌تر است. این عملیات تا زمانی که کلاس‌ها دیگر قابلیت تقسیم و کوچک شدن را نداشته باشند، ادامه پیدا می‌کند.[15]

یک نقطه ضعف در روش هیستوگرام، این است که ممکن است پیدا کردن دقیق قله‌ها و دره‌ها مشکل باشد.

روش هیستوگرام می‌تواند به سرعت برای اعمال به فریم‌ها خود را تطبیق دهد و همزمان بازده خود را حفظ کند. وقتی که فریم‌های مختلف در نظر گرفته شوند، روش هیستوگرام را می‌توان در چند حالت به تصویر اعمال کرد. همان عملیاتی که می‌تواند بر روی یک فریم اعمال شود، می‌تواند برای چند فریم هم پیاده‌سازی گردد و نهایتاً خروجی اصلی، مجموع تمامی خروجی فریم‌ها خواهدبود. قله‌ها و دره‌ها که پیش تر به سختی قابل شناسایی بودند، به سادگی تمیز داده می‌شوند. روش هیستوگرام در جایی‌که دیتای خروجی برای مشخص کردن مُد رنگ در محل پیکسل استفاده می‌شود، می‌تواند بر اساس پیکسل هم اعمال شود. این روش بخش‌بندی بر اساس اشیاء متحرک و محیط ساکن است. ازین روش در پیدا کردن موقعیت ابجکت‌های متحرک در ویدئوها، استفاده می‌شود.

آشکارسازی لبه

آشکارسازی لبه یک فیلد پیشرفته در پردازش تصویر محسوب می‌شود. مرز و لبه ناحیه‌ها به یکدیگر مرتبط هستند. در اغلب موارد در نواحی مربوط به مرزها، شدت روشنایی تغییرات سریعی نمی‌کند. آشکارسازی لبه به عنوان یک تکنیک پایه در اکثر روش‌های بخش‌بندی مورد استفاده قرار می‌گیرد.

لبه‌های شناسایی شده توسط آشکارساز لبه در اغلب موارد ناپیوسته هستند. برای جدا کردن یک شی در تصویر، پیدا کردن مرزهای آن از ملزومات است. لبه‌های مطلوب، در واقع مرز بین این اشیاء و تاکسون‌های فضایی می‌باشند.[16][17]

روش مبتنی بر خوشه بندی دوگانه

این روش ترکیبی از سه ویژگی در تصویر است: تقسیم‌بندی تصویر براساس آنالیز هیستوگرام توسط فشردگی بالای کلاس‌ها و گرادیان مرزهای آن کلاس‌ها، چک می‌شود. برای این منظور دو فضا باید معرفی شوند: یکی از فضاها، هیستوگرام روشنایی است (H = H(B، فضای دوم، فضای ۳ بعدی از تصویر اصلی می‌باشد (B = B(x, y. فضای اول اجازه می‌دهد تا مقدار فشردگی توزیع روشنایی‌ای که توسط روش minimal clustering kmin محاسبه می‌شود را اندازه‌گیری کنیم. آستانه روشنایی T مربوط به روش kmin تصویر باینری (سیاه و سفید) را می‌سازد – (bitmap b = φ(x, y که در آن φ(x, y) = ۰ اگر B(x, y) <T و φ(x, y) = ۱ اگر B(x, y) ≥ T باشد. بیت مپ (bitmap) یک شی در فضای دوگانه است. در آن بیت مپ معیاری برای چگونگی توزیع نقاط سیاه (یا سفید) در پیکسل‌ها باید تعریف شود؛ بنابراین هدف پیدا کردن اشیاء دارای مرزهای مطلوب است. برای تمامی Tها، معیار (MDC =G/(k×L باید محاسبه شود (که در آن k تفاوت در روشنایی بین شی و پس زمینه، L طول تمامی مرزها و G گرادیان ماینگین در مرزهاست). مقدار ماکزیمم M بخش‌بندی را مشخص می‌کند.[18]

روش رشد ناحیه

روش رشد ناحیه عمدتاً اساس خود را بر این فرض که پیکسل‌های مجاور دارای ویژگی‌های مشابهی هستند، می‌گذارد. روش کلی کار در این روش مقایسه یک پیکسل با پیکسل‌های مجاور آن است. اگر معیارهای شباهت ارضا شوند، پیکسل موردنظر می‌تواند به کلاسی که پیکسل‌های مجاور به آن تعلق دارند، اضافه شود. تعیین معیارهای شباهت بسیار مهم است و نتایج در همه موارد از نویز تأثیر می‌پذیرد.

روش‌های ادغام ناحیه‌های آماری[19] (SRM) با ساخت گرافی از پیکسل‌هایی با ۴ همسایگی، به همراه مرزهایی که با مقدار مطلق تفاوت شدت روشنایی وزن دهی شده‌اند، شروع می‌شود. با استفاده از ۴-ارتباط با لبه‌های وزنی با ارزش مطلق شدت تفاوت دارد. در ابتدا هر پیکسل، یک ناحیه متشکل از یک پیکسل را می‌سازد. سپس روش SRM، لبه‌هایی که در صف اولویت هستند را مرتب می‌کند و سرانجام تصمیم می‌گیرد که ناحیه‌هایی که متعلق به یک لبه هستند را با استفاده از پیش‌بینی آماری به یکدیگر ادغام کند یا نه.

یکی از روش‌ها رشد ناحیه، روش مبتنی بر پیدا کردن هسته اولیه ناحیه‌هاست. این روش مجموعه از هسته‌های اولیه را به عنوان ورودی اتخاذ می‌کند. هسته‌های اولیه به صورت مرتب با پیکسل‌های مجاور خود مقایسه می‌شوند. تفاوت بین شدت روشنایی پیکسل مورد بررسی و میانگین شدت روشنایی ناحیه، به عنوان معیار شباهت استفاده می‌شود.

روش‌های مبتنی بر معادله دیفرانسیل با مشتقات جزئی

با استفاده از یک روش مبتنی بر معادله دیفرانسیل با مشتقات جزئی (PDE) و حل عددی آن می‌توان تصاویر را بخش‌بندی کرد.[20] منحنی انتشار، یک روش محبوب در این زمینه با برخورداری از کاربردهای متعدد در زمینه استخراج و ردیابی اشیاء و غیره محسوب می‌شود. ایده اصلی، تکامل یک منحنی اولیه، در جهت رسیدن به کمترین مقدار تابع هزینه است. همانند اکثر روش‌های مسائل معکوس، مینیمم کردن مقدار تابع هزینه، مسئله‌ای مهمی محسوب می‌شود و محدودیت‌های مشخصی که در اینجا همان محدودیت‌های هندسی هستند را اعمال می‌کند.

روش variational

هدف از روش واریانسی، پیدا کردن بخش‌بندی‌ای است که با توجه به انرژی معین عملکردی، بهینه می‌باشد. انرژی معین عملکردی، شامل یک ترم مربوط به فیت کردن دیتا و یک ترم مربوط به رگولاریزه کردن است. یک بیان کلاسیک Potts model نام دارد که برای تصویر f به صورت زیر تعریف می‌شود:${\displaystyle \operatorname {argmin} _{u}\gamma \|\nabla u\|_{0}+\int (u-f)^{2}dx.}$

یک مینیمم‌کننده یک تصویر ثابت است که بین فاصله مربع L2 و تصویر داده شده و طول کل پرش آن مصالحه برقرار می‌کند. مجموعه پرش از بخش‌بندی را مشخص می‌کند. وزن نسبی انرژی، توسط پارامتر . متغیر باینری مدل Potts، اگر رنج تغییرات به دو مقدار محدود شده باشد، اغلب با نام Chan-Vese model شناخته می‌شود.[21] ک کلی سازی مهم Mumford-Shah model می‌باشد که رابطه آن به شرح زیر است:

${\displaystyle \operatorname {argmin} _{u,K}\gamma |K|+\mu \int _{K^{C}}|\nabla u|^{2}dx+\int (u-f)^{2}dx.}$

مقدار عملکردی، جمع تمامی منحنی‌های بخش‌بندی k است. u ضریب تخمین نرم شدگی و f فاصله آن تا تصویر اصلی است.

روش تقسیم کردن گراف

روش تقسیم‌بندی گراف، یک روش مؤثر برای بخش‌بندی تصویر محسوب می‌شود. آن‌ها تأثیر پیکسل‌های مجاور را بر یک خوشه داده شده از پیکسل‌ها، با در نظر گرفتن یکنواختی در عکس، مدل می‌کنند. در این روش، تصویر به عنوان یک گراف وزن دار غیرمستقیم، مدل می‌شود. معمولاً یک پیکسل یا گروهی از پیکسل‌ها با وزن گره‌ها و لبه‌ها در ارتباط هستند، شباهت (یا عدم شباهت) با پیکسل‌های مجاور را تعریف می‌کنند. سپس گراف (یا همان تصویر) با توجه به معیاری که برای خوشه‌بندی مطلوب، طراحی شده‌است، تقسیم‌بندی می‌شود. هر بخش از خروجی گره‌ها (پیکسل‌ها) از این الگوریتم، به عنوان یک شی جدا شده در تصویر محسوب می‌شود.

Markov random fields

کاربرد (Markov random fields (MRF در حوزه تصویر در اویل سال 1984، توسط Geman مطرح شد.[22] اصول ریاضی قوی و توانایی آن‌ها در تهیه یک بهینه کلی، حتی وقتی که بر اساس ویژگی‌های محلی تعریف شده بود، ثابت کرد که می‌تواند اساس زمینه تحقیق جدید در حوزه تحیلیل تصویر، رفع نویز و بخش‌بندی باشد. MRFها کاملاً با توزیع احتمال پیشین، نظریه گراف و توزیع احتمال حاشیه‌ای خود توصیف می‌شوند. معیار بخش‌بندی تصویر با استفاده از MRF به عنوان پیدا کردن طرح برچسب گذاری‌ای که بیشترین احتمال برای یک مجموعه از ویژگی‌های مشخص را دارد، مطرح می‌شود. دسته گسترده‌ای از روش‌های بخش‌بندی تصویر با استفاده از MRFها، می‌تواند بخش‌بندی‌های با نظارت یا بدون نظارت هستند.

بخش‌بندی با نظارت با استفاده از MRF و MAP

در زمینه بخش‌بندی، تابعی که الگوریتم MRF به دنبال ماکزیمم کردن آن است، احتمال تشخیص یک طرح برچسب گذاری با توجه به مجموعه از ویژگی هاست شناسایی شده در تصویر، می‌باشد. این موضوع بیان دیگری از روش برآوردگر بیشینه‌گر احتمال پسین است.

همسایگی MRF برای یک پیکسل مشخص

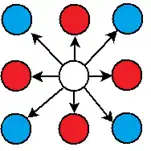
همسایگی MRF برای یک پیکسل مشخص

مراحل الگوریتم ژنتیک برای یخش بندی تصویر با استفاده از MAP در زیر آورده شده‌است:

1. همسایگی هر ویژگی را تعریف کنید. در حالت کلی این مجاورت شامل هماسیگی های مرتبه اول و دوم می شود.
2. احتمال اولیه P(f_i) برای هر ویژگی را تعیین کنید
3. که در آن f_i ∈ Σ مجموعه‌هایی هستند که شامل ویژگی های استخراج شده برای پیکسل i ام می‌باشند و کلاس‌های اولیه را تعریف می‌کنند.
4. با استفاده از دیتای اموزشی میانگین (μ_li) و واریانس (σ_li) برای هر پیکسل قابل محاسبه خواهد بود.
5. تابع احتمال حاشیه‌ای P(f_i|l_i) را با استفاده از تئوری بیز، برای هر طرح برچسب گذاری محاسبه کنید. مدل گوسین زیر برای محاسبه احتمال حاشیه ای مورد استفاده قرار می‌گیرد.

   ${\displaystyle {\frac {1}{\sigma (l_{i}){\sqrt {2\pi }}}}e^{-{\frac {(f_{i}-\mu (l_{i}))^{2}}{2\sigma (l_{i})^{2}}}}}$

6. احتمال برچسب هر کلاس را با توجه به همسایگی تعریف شده در مراحل قبل، محاسبه کنید
7. احتمالات پیشین جدید را تکرار کنید و کلاس ها را به نحوی بازتعریف کنید که مقادیر این احتمالات ماکزیمم شود.این مرحله با استفاده از بسیاری از الگوریتم های بهینه ساز قابل اجرا خواه بود.
8. زمانی که مقادیر توابع احتمال ماکزیمم شد و برچسب هیچ کلاسی تغییر نکرد، عملیات را متوقف کنید.

یک گراف بدون جهت یا مارکوفی را می‌توان به صورت <G=<V,E نوشت به‌طوریکه V مجموعه گره‌ها و E مجموعه‌ی تمام یال‌ها در گراف است. گره‌های یک گراف را می‌توان در یک گراف مربوط به عکس به دو دسته تقسیم کرد. گره‌هایی که در همسایگی هم قرار دارند و درواقع همان پیکسل‌های تصویر هست و ۲ گره دیگر به نام S,T کهS در عکس ُ‌نماینده گره‌هاییست که شی موردنظر را نمایش می‌دهند و T نماینده پس‌زمینه است. این نوع گراف را گراف S,T هم می‌نامند.

در این گراف یال‌ها هم شامل چند دسته‌اند:nlink که یال‌ها بین پیکسل‌های همسایه هستند و tlink که گره t یا همان terminal را به گره‌های تصویر متصل م‌کند. در این نوع گراف‌ها وزن‌ها همواره غیر منفی درنظر گرفته می‌شوند. یک کات در گراف یک زیرمجموعه از یال‌هاست و با C معرفی می‌شود. هزینه هر کات معادل مجموع وزن یال‌هاییست که در آن کات واقع شده است. کات کمینه به برشی گفته می‌شود که این هزینه در آن برش مینیمم شود. پیدا کردن برش کمینه معادل پیدا کردن maxflow در گراف است. برای segmentation می‌توان به گره S برچسب ۱ و به گره‌های t که همان پس‌زمینه هستند برچسب۰ نسبت داد و عملیات segmentation را به صورت کمینه کردن انرژی در این MRF محاسبه کرد. مسائل گراف کات در بینایی را می‌توان به صورت یک مسئله حداقل کردن انرژی درنظر گرفت. در اینجا ما به دنبال یافتن برچسب f هستیم که انرژی را به حداقل برساند.

${\displaystyle E(f)=E_{smooth}(f)+E_{data}(f)}$

ٍE_smooth تشابه f با برچسب پیکسل‌های اطراف و E_data اختلاف f با داده‌های مشاهده شده را نشان می‌دهد.

انرژی داده به روش‌های مختلفی محاسبه می‌شود اما درحالت کلی میزان شباهت پیکسل و برچسب آن برای محاسبه انرژی مورد بررسی قرار می‌گیرد. انتخاب E_smooth یک مسئله بحرانی است و انتخاب‌های زیادی هم برای آن وجود دارد مثلاً در بعضی روش‌ها همیشه f را شبیه همسایگان انتخاب می‌کنند که این باعث نتایج ضعیف در مرز بین شی‌های تصویر می‌شود. توابع انرژی که این مشکل را ندارند، توابع discontinuity preserving نامیده می‌شوند. مشکل اصلی در اینجا هزینه محاسباتی بالاست به این دلیل که فضای انتخاب برچسب بسیار بزرگ است و دارای هزاران برچسب مختلف هستیم. از طرفی این مسئله دارای مینیمم‌های محلی زیادیست. توابع انرژی که ما درنظر گرفتیم به صورت زیر است:

${\displaystyle E(f)=\sum _{p}D_{p}(f_{p})+\sum _{N}V_{p,q}(f_{p},f_{q})}$

N مجموعه جفت پیکسل‌هایی که با هم در ارتباطند. معمولاً این ارتباطات بین دو پیکسل همسایه درنظر گرفته می‌شود، همچنین معمولاً مقدار D_data غیر منفی است. مقدار هرکدام ازVها می‌تواند متفاوت باشد و بستگی به کاربرد دارد. این دو الگوریتم مینیمم کردن انرژی را براساس دو دسته کلاس از V می‌توانند انجام دهند. کلاس‌های سمیمتریک و متریک (ریاضیات) که هردوی این کلاس‌ها باعث ایجاد توابعی که دارای خاصیت discontinuity preserving هستند، می‌شود.

الگوریتم گسترش آلفا

ایده اصلی در الگوریتم گسترش آلفا، پیداکردن روش مناسب دسته‌بندی پیکسل‌ها بوسیله‌ی تنها دوبرچسب آلفا و غیرآلفا بااستفاده از الگوریتم گراف کات است. در این الگوریتم در هر مرحله، مقدار آلفا تغییر می‌کند تا تمام برچسب‌ها پوشش داده‌شوند. ساختار این گراف که درواقع یک گراف s_t است در هر مرحله از الگوریتم، بوسیله‌ی برچسب آلفا مشخص می‌شود. در نتیجه این ساختار به صورت پویا درحال تغییر است. در ابتدا گراف بوسیله‌ی برچسب‌بندی اولیه‌ی f و مقدار آلفا ساخته می‌شود. سپس به کمک جدول موجود در شکل جدول وزن‌های مربوط به گسترش آلفا که نحوه وزن‌دهی به این گراف را مشخص می‌کند، برش‌های اولیه مشخص می‌شوند. برای هر آلفا برش‌بندی بهینه انتخاب شده و در مرحله‌ی بعدی به عنوان گراف ورودی آلفا بعد بررسی میشود. ساختار گراف توصیف شده در شکل گراف s-t برای الگوریتم آلفا قابل مشاهده است.

الگوریتم مبادله آلفابتا

ایده اصلی در مبادله آلفابتا، برچسب زدن صحیح به‌وسیله‌ی αوβ است و در این الگوریتم تمامی حالت‌ها برای αوβ متفاوت محاسبه خواهند شد.در هر تکرار یکی زوج αوβ بررسی می‌شود و این روند تا زمانیکه segmentation همگرا شود، ادامه می‌یابد. در هر تکرار، ناحیه‌ی مربوط به αوβ تعیین می‌شود ولی در این قسمت، گره‌هایی که مربوط به هیچکدام از αوβنباشند هم داریم. در این حالت وزن پیکسلی که عضو هیچکدام نیس، مجموع تمام لینک‌های بین این پیکسل و تمام همسایگانی است که به هیچکدام از αوβ نیست.

الگوریتم بهینه سازی

هر الگوریتم بهینه سازی، مدل تطبیق یافته‌ای از انواع مدل‌ها در زمینه‌های مختلف است که توسط توابع هزینه منحصربه‌فرد خود تنظیم شده‌اند. ویژگی مشترک توابع هزینه، تغییر مقدار و برچسب هر پیکسل در مقایسه با همسایگان آن است.

مدل تکرار شرطی

الگوریتم تکرار شرطی(ICM) سعی می‌کند طرح برچسب‌گذاری ایدئال را با تغییر مقدار هر پیکسل در یک چرخه تکرار شونده و محاسبه انرژی پرچسب‌گذاری‌های جدید که توسط تابع هزینه زیر به دست می‌آیند را بازسازی کند.

${\displaystyle \alpha (1-\delta (l_{i}-l_{{\text{initial }}i})+\beta \Sigma _{q\in N(i)}(1-\delta (l_{i},l_{q(i)}))}$

که در آن α هزینه تغییر در برچسب پیکسل و β هزینه در تفاوت در برچسب پیکسل انتخاب شده و پیکسل‌های مجاور است. در اینجا (N(i همسایگی پیکسل i و δ تابع دلتا می‌باشد. ی مشکل اصلی در ICM این است که همانند گرادیان، مقادیر آن در حدود ماکزیمم محلی ست و بنابراین یک طرح برچسب گذاری بهینه و کلی به دست نخواهد آمد.

تبدیل watershed

تبدیل watershed، دامنه گرادیان یک تصویر را به عنوان سطح توپوگرافی در نظر می‌گیرد. پیکسل‌هایی که بیشترین مقدار دامنه گرادیان را دارند، به خطوط watershed مپ می‌شوند که این خطوط نمایانگر مرز نواحی خواهندبود. آب در هر ناحیه، که توسط خطوط watershed محصور شده‌است، شروع به بالا آمدن می‌کند تا به سطح مینیمم محلی برسد. پیکسل‌هایی که آب در آن‌ها به سطح مینیمم محلی می‌رسد، یک بخش را مشخص می‌کنند.

بخش بندی مدل محور

فرض اصلی در این روش این است که ساختارهای موردنظر، دارای فرم هندسی تکرار شونده ای می‌باشند. بنابراین می‌توان برای توضیح تنوع ساختارها، یک مدل احتمالاتی را جستجو کرد. چنین عملیاتی مراحلی که در ادامه میآیند را شامل می‌شود: (i) ثبت نمونه‌های آموزشی به یک پوزیشن خاص، (ii) بیان احتمالاتی تنوع نمونه‌های ثبت شده و (iii) استنتاج آماری بین مدل ارائه شده و تصویر. هنر این مدل در بخش بندی براساس دانشی ست که از اشکال فعال، مدل‌های ظاهری، نمونه‌های شکل‌پذیر و مرزهای فعال بهره می‌برد.

یادداشت

1. Linda G. Shapiro and George C. Stockman (2001): “Computer Vision”, pp 279-325, New Jersey, Prentice-Hall, شابک ‎۰−۱۳−۰۳۰۷۹۶−۳
2. Barghout, Lauren, and Lawrence W. Lee. "Perceptual information processing system." Paravue Inc. U.S. Patent Application 10/618,543, filed July 11, 2003.
3. Pham, Dzung L.; Xu, Chenyang; Prince, Jerry L. (2000). "Current Methods in Medical Image Segmentation". Annual Review of Biomedical Engineering. 2: 315–337. doi:10.1146/annurev.bioeng.2.1.315. PMID 11701515.
4. Forghani, M.; Forouzanfar, M.; Teshnehlab, M. (2010). "Parameter optimization of improved fuzzy c-means clustering algorithm for brain MR image segmentation". Engineering Applications of Artificial Intelligence. 23 (2): 160–168.
5. W. Wu, A. Y. C. Chen, L. Zhao and J. J. Corso (2014): "Brain Tumor detection and segmentation in a CRF framework with pixel-pairwise affinity and super pixel-level features", International Journal of Computer Aided Radiology and Surgery, pp. 241-253, Vol. 9.
6. E. B. George and M. Karnan (2012): "MR Brain image segmentation using Bacteria Foraging Optimization Algorithm", International Journal of Engineering and Technology, Vol. 4.
7. Kamalakannan, Sridharan; Gururajan, Arunkumar; Sari-Sarraf, Hamed; Rodney, Long; Antani, Sameer (17 February 2010). "Double-Edge Detection of Radiographic Lumbar Vertebrae Images Using Pressurized Open DGVF Snakes". IEEE Transactions on Biomedical Engineering. 57 (6): 1325–1334. doi:10.1109/tbme.2010.2040082. Retrieved 10 February 2017.
8. J. A. Delmerico, P. David and J. J. Corso (2011): "Building façade detection, segmentation and parameter estimation for mobile robot localization and guidance", International Conference on Intelligent Robots and Systems, pp. 1632-1639.
9. Batenburg, K J.; Sijbers, J. (2009). "Adaptive thresholding of tomograms by projection distance minimization". Pattern Recognition. 42 (10): 2297–2305. doi:10.1016/j.patcog.2008.11.027.
10. Batenburg, K J.; Sijbers, J. (June 2009). "Optimal Threshold Selection for Tomogram Segmentation by Projection Distance Minimization". IEEE Transactions on Medical Imaging. 28 (5): 676–686. doi:10.1109/tmi.2008.2010437. Archived from the original (PDF) on 3 May 2013. Retrieved 5 June 2018.
11. Kashanipour, A.; Milani, N; Kashanipour, A.; Eghrary, H. (May 2008). "Robust Color Classification Using Fuzzy Rule-Based Particle Swarm Optimization" (PDF). IEEE Congress on Image and Signal Processing. 2: 110–114.
12. Barghout, Lauren; Sheynin, Jacob (2013-07-02). "Real-world scene perception and perceptual organization: Lessons from Computer Vision". Journal of Vision. 13 (9): 709–709. doi:10.1167/13.9.709. ISSN 1534-7362.
13. Hossein Mobahi; Shankar Rao; Allen Yang; Shankar Sastry; Yi Ma. (2011). "Segmentation of Natural Images by Texture and Boundary Compression" (PDF). International Journal of Computer Vision. 95: 86–98. doi:10.1007/s11263-011-0444-0. Archived from the original (PDF) on 8 August 2017. Retrieved 29 June 2018.
14. Shankar Rao, Hossein Mobahi, Allen Yang, Shankar Sastry and Yi Ma Natural Image Segmentation with Adaptive Texture and Boundary Encoding بایگانی‌شده در ۱۹ مه ۲۰۱۶ توسط Wayback Machine, Proceedings of the Asian Conference on Computer Vision (ACCV) 2009, H. Zha, R.-i. Taniguchi, and S. Maybank (Eds.), Part I, LNCS 5994, pp. 135--146, Springer.
15. Ohlander, Ron; Price, Keith; Reddy, D. Raj (1978). "Picture Segmentation Using a Recursive Region Splitting Method". Computer Graphics and Image Processing. 8 (3): 313–333. doi:10.1016/0146-664X(78)90060-6.
16. R. Kimmel and A.M. Bruckstein. http://www.cs.technion.ac.il/~ron/PAPERS/Paragios_chapter2003.pdf, International Journal of Computer Vision 2003; 53(3):225-243.
17. R. Kimmel, http://www.cs.technion.ac.il/~ron/PAPERS/laplacian_ijcv2003.pdf, chapter in Geometric Level Set Methods in Imaging, Vision and Graphics, (S. Osher, N. Paragios, Eds.), Springer Verlag, 2003. شابک ‎۰۳۸۷۹۵۴۸۸۰
18. بایگانی‌شده در ۱۳ اکتبر ۲۰۱۷ توسط Wayback MachineShelia Guberman, Vadim V. Maximov, Alex Pashintsev Gestalt and Image Understanding. GESTALT THEORY 2012, Vol. 34, No.2, 143-166.
19. R. Nock and F. Nielsen, Statistical Region Merging, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 26, No 11, pp 1452-1458, 2004.
20. Caselles, V.; Kimmel, R.; Sapiro, G. (1997). "Geodesic active contours" (PDF). International Journal of Computer Vision. 22 (1): 61–79. doi:10.1023/A:1007979827043.
21. Chan, T.F.; Vese, L. (2001). "Active contours without edges". IEEE Transactions on Image Processing. 10 (2): 266–277. doi:10.1109/83.902291.
22. S. Geman and D. Geman (1984): "Stochastic relaxation, Gibbs Distributions and Bayesian Restoration of Images", IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 721-741, Vol. 6, No.6.