توزیع کی

در نظریه امار و احتمال، توزیع احتمال chi یک توزیع پیوسته‌است. این توزیع برابر ریشه جمع مربعات مجموعه ای از متغییرهای تصادفی است که هر یک به‌طور مستقل از توزیع نرمال پیروی می‌کنند.

chi

تابع چگالی احتمال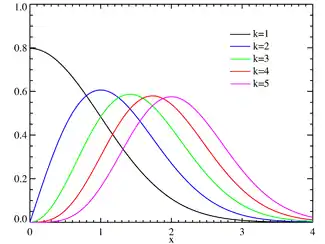
تابع توزیع تجمعی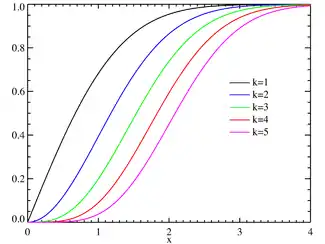
فراسنجه‌ها	${\displaystyle k>0\,}$ (درجه‌های آزادی)
تکیه‌گاه	${\displaystyle x\in [0;\infty )}$
تابع چگالی احتمال	${\displaystyle {\frac {2^{1-k/2}x^{k-1}e^{-x^{2}/2}}{\Gamma (k/2)}}}$
تابع توزیع تجمعی	${\displaystyle P(k/2,x^{2}/2)\,}$
میانگین	${\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}$
مُد	${\displaystyle {\sqrt {k-1}}\,}$ for ${\displaystyle k\geq 1}$
واریانس	${\displaystyle \sigma ^{2}=k-\mu ^{2}\,}$
چولگی	${\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}$
کشیدگی	${\displaystyle {\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}$
آنتروپی	${\displaystyle \ln(\Gamma (k/2))+\,}$ ${\displaystyle {\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}$

از توزیع‌های مشابه chi می‌توان به توزیع Rayleigh (توزیع chi با دو درجه آزادی) و توزیع ماکسول-بولتزمن در توصیف سرعت مولکول‌ها در گاز ایده‌آل (توزیع chi با سه درجع آزادی)، اشاره کرد.

اگر Xiهای k متغیر مستقل با توزیع احتمال نرمال باشند (با میانگین و واریانس ، ${\displaystyle \mu }$ و ${\displaystyle \sigma }$) حاصل عبارت زیر بیانگر توزیع chi است.

${\displaystyle Y={\sqrt {\sum _{k=1}^{k}{\biggl (}(Xi-\mu i)/\sigma i)^{2}{\Bigr )}}}}$

توزیع احتمال chi دارای پارامتری تحت عنوان درجه آزادی (k) است، که نمایانگر تعداد ---- است.

توصیف[1]

تابع چگالی احتمال

تابع چگالی احتمال(PDF) این توزیع به شکل زیر است:

${\displaystyle f(x;k)={\frac {x^{k-1}\ e^{-x^{2}/2}}{2^{k/2-1}\ \Gamma (k/2)}}}$

که در آن ${\displaystyle \Gamma }$ نمایشگر تابع گاما است.

تابع توزیع احتمال تجمعی

تابع توزیع تجمعی(CDF) این توزیع از رابطه زیر قابل محاسبه است:

${\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}$

در این رابطه تابع ${\displaystyle P}$ معادل تابع گامای ناکامل است.

پیاده‌سازی در R[2]

متودهای این توزیع، در r، با افزودن کتابخانه chi به محیط کار قابل استفاده هستند. این متودها شامل موارد زیر هستند:

dchi(x, df, ncp = 0, log = FALSE)
pchi(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qchi(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
rchi(n, df, ncp = 0)

x, q vector of quantiles.
df degrees of freedom (non-negative, but can be non-integer).
ncp non-centrality parameter (non-negative).
log, log.p logical; if TRUE, probabilities p are given as log(p).
lower.tail logical; if TRUE (default), probabilities are P[X <= x] otherwise, P[X > x].
p vector of probabilities.
n number of observations. If length(n) > 1, the length is taken to be the number
required.

مثال

s <- seq(0, 5, 0.1)
plot( dchi(s, 3), type = ‘b’, col = “red”)

قطعه کد بالا نمودار زیر را در plot چاپ می‌کند.

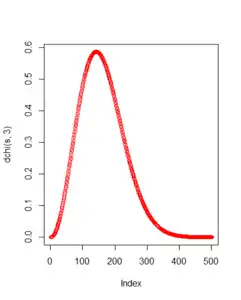
انواع توزیع کی

منابع

1. "Chi distribution". Wikipedia. 2018-06-21.
2. «Chi library» (PDF).

• Weisstein, Eric W. "Chi Distribution." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ChiDistribution.html