جدول کارنو
جدول کارنو (به انگلیسی: Karnaugh map) (اختصاری KM یا K-map) روشی است برای سادهسازی توابع جبر بولی که به وسیلهٔ موریس کارنو در سال ۱۹۵۳ ارائه شد. این روش کامل شده دیاگرام ویچ است که در سال ۱۹۵۲ توسط ادوارد ویچ ارائه شده بود. جدول کارنو نیاز به محاسبات طولانی را کاهش داده و به مشخص کردن و حذف کردن سریع وضعیت رقابتی کمک میکند.

مقادیر بولی از جدول ارزش و با توجه به اصول کد گری به جدول کارنو انتقال مییابند. دادهها در جدول کارنو که ۲n سلول دارد چیده میشوند و مینترمها بر اساس اصول جبر بول ساخته میشوند.
جدول کارنو نموداری از مربعها است که هر مربع یک مینترم را نمایش میدهد. به کمک این مربعها میتوان یک تابع بول را نمایش داد. جدول کارنو به چند حالت مختلف دو، سه، چهار و گاهی پنج متغیره نمایش مییابد. جدول کارنوی n متغیره، دارای 2n خانه است که هر خانه یک مینترم را نمایش میدهد. بعد از اینکه مینترمهای یک تابع را در جدول کارنو علامتگذاری کردیم، میتوانیم مربعهای همجوار را با هم ساده کنیم. در شکل زیر یک نقشه ۴ متغیره که ۱۶ مربع یا خانه دارد نمایش داده شدهاست:
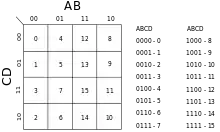
برای شمارهگذاری خانهها از کد گری استفاده شدهاست. چرا که در کد گری، هر عدد با اعداد ماقبل و مابعد خود تنها در یک رقم تفاوت دارد و این خاصیت به ساده کردن توابع بول کمک میکند.
مثال
مثال زیر یک تابع ساده نشده جبر بول را با متغیرهای بولی A,B،C,D نشان میدهد.
جدول صحت تابع به صورت زیر ساخته میشود:
| # | |||||
|---|---|---|---|---|---|
| ۰ | ۰ | ۰ | ۰ | ۰ | ۰ |
| ۱ | ۰ | ۰ | ۰ | ۱ | ۰ |
| ۲ | ۰ | ۰ | ۱ | ۰ | ۰ |
| ۳ | ۰ | ۰ | ۱ | ۱ | ۰ |
| ۴ | ۰ | ۱ | ۰ | ۰ | ۰ |
| ۵ | ۰ | ۱ | ۰ | ۱ | ۰ |
| ۶ | ۰ | ۱ | ۱ | ۰ | ۱ |
| ۷ | ۰ | ۱ | ۱ | ۱ | ۰ |
| ۸ | ۱ | ۰ | ۰ | ۰ | ۱ |
| ۹ | ۱ | ۰ | ۰ | ۱ | ۱ |
| ۱۰ | ۱ | ۰ | ۱ | ۰ | ۱ |
| ۱۱ | ۱ | ۰ | ۱ | ۱ | ۱ |
| ۱۲ | ۱ | ۱ | ۰ | ۰ | ۱ |
| ۱۳ | ۱ | ۱ | ۰ | ۱ | ۱ |
| ۱۴ | ۱ | ۱ | ۱ | ۰ | ۱ |
| ۱۵ | ۱ | ۱ | ۱ | ۱ | ۰ |
تابع فوق با دو نماد گذاری در زیر نمایش داده شدهاست. در اولی ها مینترم نامیده میشوند که شماره سطرهایی که در جدول درستی مقدار یک دارند را نمایش میدهند و در نماد گذاری دوم ها ماکسترم هستند و نمایانگر شماره سطرهایی که در جدول درستی مقدار صفر دارند هستند.
جدول کارنو
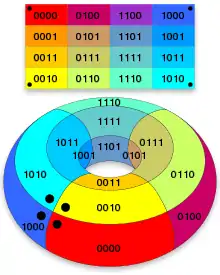
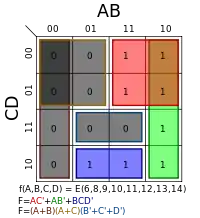
در مثال بالا، برای جدول کارنو چهار متغیره ۱۶ حالت وجود دارد و در نتیجه جدول درستی آن ۱۶ سطر دارد. جدول کارنو در یک صفحه مشبک ۴*۴ تنظیم میشود.
در این جدول شماره گذاری حاشیه جدول به ترتیب کد گری است و نه ترتیب باینری اعداد. اینگونه شماره گذاری باعث میشود اعداد مجاور در حاشیه جدول تنها در یک بیت تفاوت داشته باشند. هر سلول جدول حاوی یک عدد باینری است که خروجی تابع به ازای ترکیب خاصی از ورودیها را مشخص میکند.
بعد از اینکه جدول کارنو ساخته شد از آن برای ساده کردن جدول درستی استفاده میشود. با دستهبندی اعداد ۱ مجاور در جدول میتوان سادهسازی را انجام داد. دستهبندیها باید مستطیلی باشند به طوری که مساحت آنها توانی از دو باشد. این گروها باید تا حد امکان بزرگ باشند و حاوی صفر نباشند. ممکن است گروهها همپوشانی داشته باشند. گروهبندی بهینه در مثال زیر با گروههای سبز و قرمز و آبی مشخص شدهاند و گروه قرمز و سبز همپوشانی دارند. گروه قرمز به شکل یک مربع ۲*۲ و گروه سبز یک مستطیل ۱*۴ است. ناحیه همپوشانی نیز با رنگ قهوه ای مشخص شدهاست.
برای توصیف خروجی جدول از نماد گذاری خاصی استفاده میشود؛ مثلاً AD به ناحیه ۲*۲ اشاره میکند همزمان A و D ارزش درست دارند (خانههای ۱۳, ۹, ۱۵, ۱۱). مشابها 'AD یعنی ناحیه ای که A ارزش درست و D ارزش نادرست دارند.
خانههای جدول به شکل یک چنبره با هم همسایه اند؛ بنابراین لبههای راست و چپ با هم و لبههای بالا و پایین جدول با یکدیگر همسایه اند. همچنین چهار گوشه جدول نیز با یکدیگر همسایه اند.
شرح راه حل مثال
وقتی جدول کارنو ساخته شد و دستهبندی صورت گرفت باید عبارت جبری متناظر با هر دسته نوشته شود. بهطور مثال برای گروه قرمز:
- چون در سراسر گروهبندی قرمز ارزش A یک است بنابراین عبارت جبری متناظر این گروه باید شامل A باشد.
- از طرف دیگر B تغییر وضعیت میدهد بنابراین نباید در عبارت جبری گروه قرمز بیاید.
- C تغییر وضعیت نمیدهد و همواره صفر است؛ بنابراین عبارت جبری گروه قرمز شامل 'C است.
- D تغییر می کند پس مشمول نمیشود.
بنابراین اولین مینترم در جمع حاصل ضربها 'AC است. مشابهها برای برای گروهبندیهای سبز و آبی عبارت جبری بدست میآید:
- سلولهای آبی: 'BCD
- سلولهای قهوهای و سبز: 'AB
- سلولهای قرمز و قهوه ای: 'AC
نتیجه ترکیب گروهها مانند روبرو است: .
میتوان با استفاده از اصول و اتحادهای جبر بول عبارت ساده شده را اثبات کرد:
وارون
وارون کردن یک تابع بهطور مشابه، با دستهبندی صفرها در جدول انجام میشود. این سه دستهبندی در شکل با رنگ خاکستری و با رنگ حاشیه متفاوت مشخص شدهاند:

- قهوه ای: 'A'B
- طلایی: 'A'C
- آبی: BCD
که این تابع وارون را نتیجه میدهد:
از طریق قانون دمورگان، حاصل جمع حاصل ضربها مشخص میشود:
حالات بیتفاوت
جدول کارنو امکان سادهسازی راحت تر توابعی را فراهم میکند که شامل حالات بیتفاوت هستند. یک حالت بیتفاوت حالتی است که در آن برای طراح، خروجی آن فرقی نمیکند؛ بنابراین حالات بیتفاوت میتوانند شامل هر دستهبندی باشند که آن را بزرگتر میکند. معمولاً در جدول کارنو این حالات را با خط تیره یا X مشخص میکنیم.
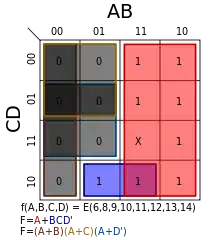
مثال سمت چپ مشابه مثال قبلی میباشد با این تفاوت که مقدار f(1,1,1,1) بیتفاوت فرض شدهاست. این باعث میشود دسته قرمز بزرگتر شود و دسته سبز حذف شود. این کار تابع بهینه جدیدی را نتیجه میدهد:
توجه کنید که عبارت اول تنها A است و نه 'A'C. در این صورت، حالت بدون تفاوت موجب شده عبارتی که از دسته سبز نتیجه میشد، حذف شود و عبارت حاصل از دستهبندی قرمز سادهتر و حالت رقابتی بخش زرد حذف شود. ساده شده تابع وارون نیز به شکل زیر است:
جدول کارنو دو-متغیره
در زیر تمام نقشههای کارنو دو متغیره ۲*۲ با مینترمها و تابع ساده شده آمدهاست:
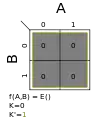 Σm(0); K = 0
Σm(0); K = 0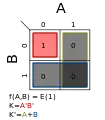 Σm(1); K = A′B′
Σm(1); K = A′B′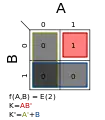 Σm(2); K = AB′
Σm(2); K = AB′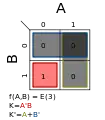 Σm(3); K = A′B
Σm(3); K = A′B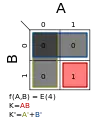 Σm(4); K = AB
Σm(4); K = AB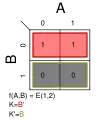 Σm(1,2); K = B′
Σm(1,2); K = B′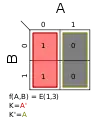 Σm(1,3); K = A′
Σm(1,3); K = A′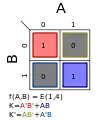 Σm(1,4); K = A′B′ + AB
Σm(1,4); K = A′B′ + AB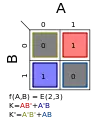 Σm(2,3); K = AB′ + A′B
Σm(2,3); K = AB′ + A′B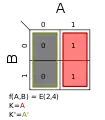 Σm(2,4); K = A
Σm(2,4); K = A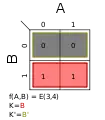 Σm(3,4); K = B
Σm(3,4); K = B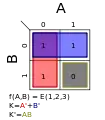 Σm(1,2,3); K = A' + B′
Σm(1,2,3); K = A' + B′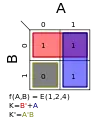 Σm(1,2,4); K = A + B′
Σm(1,2,4); K = A + B′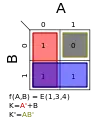 Σm(1,3,4); K = A′ + B
Σm(1,3,4); K = A′ + B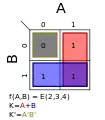 Σm(2,3,4); K = A + B
Σm(2,3,4); K = A + B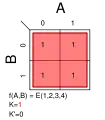 Σm(1,2,3,4); K = 1
Σm(1,2,3,4); K = 1
منابع
- مشارکتکنندگان ویکیپدیا. «Karnaugh map». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲ژوئیه ۲۰۱۱.