داده‌های گم‌شده

در آمار، داده‌های گم‌شده یا مقدارهای گم‌شده زمانی رخ می‌دهد؛ که هیچ مقدار داده‌ای برای یک متغیر در یک مشاهده ذخیره نشده باشد. داده‌های گم‌شده اتفاقی رایج است و می‌تواند اثر معنی‌داری از نتایج حاصل از داده‌ها داشته باشد.

داده‌های گم‌شده می‌توانند به‌دلیل بی‌پاسخی آماری رخ‌دهند: یعنی هیچ اطلاعاتی برای یک یا چند مورد در کل واحد («موضوع») به‌دست نیامده باشد. بعضی موارد به احتمال بیشتری بی‌پاسخی تولید می‌کنند: برای مثال مواردی که در مورد مسائل خصوصی مانند درآمد هستند. ساییدگی نوعی از دست‌رفتن که در مطالعات جغرافیایی رخ دهد. برای نمونه مطالعهٔ توسعه که اندازه‌گیری بعد از دوره‌ای از زمان تکرار شده‌است. ازدست‌رفتگی زمانی که یکی از شرکت‌کنندگان قبل از پایان مطالعه را ترک می‌کند، یا یک یا چند اندازه‌گیری از دست می‌رود، رخ می‌دهد.

داده‌ها اغلب در تحقیقات اقتصادی، جامعه‌شناسی و علوم سیاسی از بین می‌روند، زیرا دولت یا نهادهای خصوصی گزارش‌های حساس را ناقص ارائه دهند، یا کلاً ارائه ندهند،[1] یا به این علت که داده‌ها در دسترس نیستند ارائه داده نمی‌شود. بعضی مواقع گم‌شده بودن داده‌ها به‌خاطر خود محقق است، برای مثال، هنگامی که جمع‌آوری داده‌ها نامناسب است یا [در سیستم‌های اطلاعاتی] به اشتباه وارد می‌شوند.[2]

این شکل‌های بسته به نوع اثری که بر صحت نتیجه‌گیری‌های یک تحقیق می‌گذارند، انواع مختلفی دارند که عبارت‌اند از: به‌طور کامل ازدست‌رفته و به‌طور تصادفی ازدست‌رفته. می‌توان با داده‌های گم‌شده همانند داده‌های سانسورشده رفتار کرد.

انواع داده‌های گم‌شده

فهمیدن دلیل این‌که چرا داده‌ها گم‌شده‌اند برای مدیریت صحیح سایر داده‌ها مهم است. اگر داده‌ها کاملاً به‌تصادف گم‌شده باشند، نمونهٔ داده‌ها احتمالاً هنوز نماینده‌ای جامعه خواهد بود. اما اگه داده‌ها به شکل سیستماتیک گم‌شده باشند. تحلیل ممکن است اریب باشد. برای مثال، در مطالعهٔ ارتباط بین IQ و درآمد، اگر شرکت‌کنندگان با IQ متوسط به بالا تمایل به پاسخ ندادن به سؤال «درآمد شما چقدر است؟» نداشته باشند، تحلیلی که این مسئله را به‌عنوان یک الگوی گم‌شدن به‌صورت تصادفی (الگوی MAR) در نظر نمی‌گیرد، ممکن است در پیدا کردن همبستگی بین حقوق و IQ شکست بخورد. به‌خاطر این مشکلات، روش‌شناسان به‌طور معمول به محققان توصیه می‌کنند مطالعات را طراحی کنند تا وقوع داده‌های گم‌شده را به حداقل برسانند. مدل‌های گرافیکی می‌توانند با جزییات، سازوکار داده‌های گم‌شده را توصیف کنند.[3]

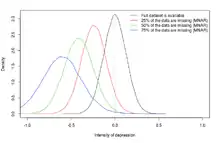
این نمودار توزیع احتمال برآورد شدت مورد انتظار افسردگی در جامعه را نشان می‌دهد. تعداد موارد ۶۰ است. فرض کنید جامعه اصلی یک توزیه نرمال باشد و احتمال بی‌پاسخی تابعی لجستیک از شدت افسردگی باشد. نتیجه این است که: هر چه دادهٔ بیشتری گم‌شده باشد (MNAR)، برآوردها اریب‌تر هستند و ما شدت افسردگی در جامعه را دست‌کم می‌گیریم.

گم‌شده به‌صورت کاملاً تصادفی

مقدارهای درون مجموعه‌داده‌ها به‌صورت کاملاً تصادفی گم‌شده (MCAR) هستند، اگر رویدادهایی که منجر به گم‌شدن هر نوع مورد-داده‌ای می‌شوند از متغیرهای قابل مشاهده و پارامترهای مورد علاقهٔ غیرقابل مشاهده مستقل باشند و به‌شکل کاملاً تصادفی رخ دهند.[4] هنگامی که داده‌ها MCAR هستند، تحلیل انجام‌شده روی داده‌ها نااریب است، گرچه داده‌ها به ندرت MCAR هستند

در مورد MCAR، از دست‌رفتگی داده‌ها، از هر متغیر دیگر مستقل است؛ بنابراین، شرکت‌کنندگان با داده‌های کامل مشاهده‌شده در اثر، یک نمونه تصادفی از همه شرکت‌کنندگان مربوط یک مداخلهٔ خاص هستند. با MCAR، تخصیص تصادفی تیمارها، محفوظ فرض می‌شود، اما معمولاً در عمل این فرضی قوی و غیرواقع‌بینانه است.[5]

گم‌شده به‌طور تصادفی



گم‌شده به‌طور تصادفی (MAR) هنگامی رخ می‌دهد که از دست‌رفتگی تصادفی نباشد، اما ازدست‌رفتگی می‌تواند به حساب متغیری که در آن اطلاعات کاملی باشد اطلاق شود.[6] MAR فرضی است که تأیید آماری آن غیرممکن است، و بر فرض معقول بودن آن اعتماد می‌شود.[7] یک مثال این است که مردها کمتر احتمال دارد که در یک مطالعه در مورد افسردگی شرکت کنند، حال آن‌که این مسئله هیچ ربطی به سطح افسردگیشان ندارد. بسته به روش تحلیل، این داده‌ها به‌دلیل خالی‌بودن شرطی سلول‌ها منجر به اریبی در تحلیل شوند (در مردها افسردگی خیلی زیاد ممکن است هیچ ورودی‌ای نداشته باشد). به‌هرحال، اگر پارامتر با برآورد درستنمایی بیشینه اطلاعات کامل برآورد شود، MAR برآوردهایی به‌طور مجانبی:نظریه مجانبی نااریب ارائه می‌دهد.

گم‌شده به‌صورت غیرتصادفی




گم‌شده به‌صورت غیرتصادفی (MNAR) (که به‌عنوان بی‌پاسخی غیرقابل چشم‌پوشی هم شناخته می‌شود) داده‌هایی هستند که نه MAR و نه MCAR باشند (برای مثال مقداری از متغیر که به دلیل مشخص گم‌شده باشد). برای توسیع مثال قبل، اگر مردان به‌خاطر سطح افسردگیشان نتوانند پرسشنامهٔ افسردگی را پرکنند.

روش‌های کار با داده‌های گم‌شده

داده‌های گم‌شده میزان نمایندهٔ جامعه بودنِ نمونه را کاهش می‌دهند، و بنابراین می‌توانند استنباط در مورد جامعه دچار مشکل کنند. به‌طور کلی، سه رویکرد کلی برای مقابله با داده‌های گم‌شده وجود دارد: جانهی -که به پرکردن جای داده‌های گم‌شده می‌گویند- حذف—که در آن نمونه‌ها با داده‌های نامعتبر از تحلیل دور انداخته می‌شوند و تحلیلی -به‌کار بردند روش‌هایی بی‌تأثیر از داده‌های گم‌شده-.

در برخی موارد کاربردی، آزمایش‌گرها می‌تواند سطح گم‌شدگی داده‌ها را کنترل کنند و از دست‌رفتگی داده‌ها قبل از جمع‌آوری داده‌ها پیش‌گیری کنند. برای مثال، در پرسشنامه‌های کامپیوتری، معمولاً جواب ندادن سؤال‌ها غیرممکن است. به این شکل که یک سؤال باید جواب داده‌شود وگرنه نمی‌توان سؤال بعدی را جواب داد؛ بنابراین گم‌شدگی داده‌ها توسط شرکت‌کنندگان با این نوع پرسشنامه ممکن نیست، اگرچه این نوع پرسشنامه ممکن است این روش در مشی اخلاقی هیئت نظارت بر آن پژوهش مجاز نباشد. در تحقیقات، چندین تلاش برای تماس با شرکت‌کنندگان، اغلب از طریق ارسال نامه، برای ترغیب افرادی که تصمیم به شرکت نکردن در مطالعه گرفته‌اند، برای تغیر تصمیمشان، در مطالعه امری مرسوم است.[8]:161–187 بااین‌حال، این روش‌ها هم می‌تواند در کاهش آثار مخرب استنباطی داده‌های گم‌شده کمک کند و هم آسیب بزند، زیرا نوع افرادی که قرار است بعد از رد اولیه شرکتشان در مطالعه برای شرکت‌کردن مجدد متقاعد شوند، به‌طور معنی‌دار متفاوت از نوع افرادیست که پس از درخواست مجدد از آن‌ها برای شرکت در مطالعه، درخواست را رد می‌کنند..:188–198

در شرایطی که وقوع داده‌های گم‌شده محتمل است، محققان معمولاً به استفاده از روش‌های آماری مقاوم در برابر گم‌شدگی داده‌ها توصیه می‌شوند. یک تحلیل وقتی مقاوم است که ما مطمئن باشیم تغییرات خفیف تا متوسط فرضیات تکنیکی کلیدی یا اریبی ایجاد نمی‌کند یا مقدار کمی اریبی ایجاد می‌کند، یا تحریف در نتایج در مورد جمعیت است.

جانهی

برخی روش‌های تجزیه و تحلیل داده‌ها در برابر داده‌های گم‌شده مقاوم نیستند و نیاز به «پر کردن»، یا جانهی مقدار گم‌شده دارند. روبین (۱۹۸۷) استدلال کرد که تکرار جانهی حتی برای تعداد اندک (۵ یا کمتر) تا حد زیادی کیفیت برآورد را بهبود می‌بخشد. برای اهداف زیادی، ۲ یا ۳ جانهی برای بسیاری از اهداف عملی ۲ یا 3 imputations تصرف بسیاری از نسبی بهره‌وری است که می‌تواند گرفته شده با تعداد زیادی از imputations. اما بیش از حد تعداد کمی از imputations می‌تواند منجر به از دست دادن قابل توجهی از آماری قدرتو برخی از محققان در حال حاضر توصیه می‌کنند ۲۰ تا ۱۰۰ یا بیشتر.[9] هر ضرب-منسوب تجزیه و تحلیل داده‌ها باید تکرار برای هر یک از منسوب مجموعه داده و در برخی موارد مربوط به آمار باید ترکیب نسبتاً پیچیده در راه است.

الگوریتم امید ریاضی–بیشینه کردن (EM) رویکردی است که مقادیر آماره‌ها که در صورت کامل بودن یک مجموعه‌داده برآورد می‌شود (جانهی می‌شود)، با توجه به الگوی داده‌های گم‌شده. در این روی‌کرد، مقدار داده‌های گم‌شده تکی به‌طور معمول جانهی نمی‌شوند.

درون‌یابی

در شاخهٔ ریاضیاتی آنالیز عددی، درون‌یابی روش ساخت روش ساخت نقطه داده‌های جدید در یک بازهٔ مجموعه‌ای گسسته از نقاط داده‌ای شناخته شده‌است.

در مقایسه دو نمونهٔ زوجی شامل داده‌های گم‌شده، یک آماره آزمون که از همه داده‌های موجود بدون نیاز به جانهی استفاده می‌کند، آزمون تی استیودنت برای نمونه‌های به‌طور جزئی دارای هم‌پوشانی است.[10] این آزمون تحت شرط نرمال بودن و فرض MCAR معتبر است.

حذف جزئی

روش‌هایی که شامل محدود کردن یک مجموعه‌داده به داده‌هایی بدون داده‌های گم‌شدگی که شامل این موارد می‌شوند:

  • حذف لیستی/حذف موردی
  • حذف روجی

تحلیل کامل

روش‌هایی که از همهٔ اطلاعات موجود، بدون اعوجاج نتایج حاصل مقدارهای جانهی شده به‌عنوان حالتی که در واقع مشاهده می‌شوند، به‌کارگیری می‌کند.

  • رویکردهای مولد:
    • الگوریتم امید ریاضی–بیشینه کردن
    • برآورد بیشینهٔ درستنماییی اطلاعات کامل
  • رویکردهای افتراقی:
    • طبقه‌بندی حداکثر-حاشیه داده‌ها با ویژگی‌ها ناموجود[11]

روش‌های مبتنی بر مدل

روش‌های مبتنی بر مدل، غالباً با استفاده از نمودار، ابزارهای دیگری برای تست داده‌های گم‌شده و برای برآورد پارامترها تحت شرایطی که داده‌های گم‌شده وجود دارندپیشنهاد می‌دهند (MCAR, MAR و MNAR). برای مثال، یک تست برای رد کردن MAR/MCAR به‌شرح زیر است:

برای هرکدام از سه‌متغیر X, Y و Z که Z کاملاً مشاهده شده‌است و X و Y به‌طور جزئی مشاهده شده‌اند، دادها باید در شرط

به بیان دیگر، مشاهدهٔ جزئی X باید مستقل از وضعیت گم‌شدگی Y، به شرط هر مقدار Z باشد. برقرار نشدن این شرط بیان‌گر این است که مسئله متعلق به دستهٔ MNAR است.[12]

(نکته: این آزمون‌ها برای MAR مبتنی بر متغیر که تغییر کمی نسبت به MAR مبتنی بر رویداد دارند لازم‌اند.[13][14][15])

هنگامی که داده‌ها در دستهٔ MNAR قرار می‌گیرند، روش‌هایی برای برآورد سازگار پارامترها در شرایط خاص مدل در دسترس هستند.[16] برای مثال اگر Y که بیانگر دلیل گم‌شدگی در X, Y است، خود دارای داده‌های گم‌شده باشد، هنوز هم توزیع احتمال توأم X و Y در صورتی که گم‌شدگی Y تصادفی باشد می‌تواند برآورد شود. برآورد در این حالت به این شکل خواهد بود:

که در آن و

ساختارهای متفاوت هر زمان که برآوردهای سازگار ممکن است، منجر به برآوردهای متفاوت و فرایندهای متفاوت برآورد شود. مورد برآورد قبل اول با برآورد از اطلاعات کامل و ضرب آن در

در بسیاری از موارد روش‌های مبتنی بر مدل به ساختار مدل این اجازه را می‌دهد تا تحت آزمون‌های نادرستی قرار گیرد. هر مدلی که استفلال بین متغیر به‌طور جزئی مشاهده شدهٔ X و شاخص گم‌شدگی متغیر دیگر Y را ایجاب کند، (یعنی ) به شرط

در نهایت، برآوردشده‌هایی که از این روش‌ها می‌آیند از فرم بسته می‌آیند و نیاز به فراینده‌های تکراری مانند الگوریتم امید ریاضی–بیشینه کردن ندارند.[17]

یک کلاس خاص از مشکلات هنگامی که احتمال گم‌شدگی به زمان وابسته است ظاهر می‌شود. برای مثال، در پایگاه دادهٔ تروما، احتمال از دست‌رفتن داده‌های مربوط به تروما وابسته به زمان روز بعد از تروماست. در این موارد مدل‌های زنجیره ای مارکوف ناایستای متنوعی اعمال می‌شود.[18]

جستارهای وابسته

منابع
  1. Messner SF (1992). "Exploring the Consequences of Erratic Data Reporting for Cross-National Research on Homicide". Journal of Quantitative Criminology. 8 (2): 155–173. doi:10.1007/bf01066742.
  2. Hand, David J.; Adèr, Herman J.; Mellenbergh, Gideon J. (2008). Advising on Research Methods: A Consultant's Companion. Huizen, Netherlands: Johannes van Kessel. pp. 305–332. ISBN 90-79418-01-3.
  3. Karvanen, Juha (2015). "Study design in causal models". Scandinavian Journal of Statistics. 42 (2): 361&ndash, 377. arXiv:1211.2958. doi:10.1111/sjos.12110.
  4. Polit DF Beck CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed. Philadelphia, USA: Wolters Klower Health, Lippincott Williams & Wilkins.
  5. Deng. "On Biostatistics and Clinical Trials". Archived from the original on 15 March 2016. Retrieved 13 May 2016.
  6. "Archived copy". Archived from the original on 2015-09-10. Retrieved 2015-08-01.CS1 maint: Archived copy as title (link)
  7. Little, Roderick (2002). Statistical analysis with missing data. Hoboken, N.J: Wiley. ISBN 978-0-471-18386-0.
  8. Stoop, I.; Billiet, J.; Koch, A.; Fitzgerald, R. (2010). Reducing Survey Nonresponse: Lessons Learned from the European Social Survey. Oxford: Wiley-Blackwell. ISBN 0-470-51669-0.
  9. Graham J.W.; Olchowski A.E.; Gilreath T.D. (2007). "How Many Imputations Are Really Needed? Some Practical Clarifications of Multiple Imputation Theory". Preventative Science. 8 (3): 208–213. doi:10.1007/s11121-007-0070-9.
  10. Derrick, B; Russ, B; Toher, D; White, P (2017). "Test Statistics for the Comparison of Means for Two Samples That Include Both Paired and Independent Observations". JMASM. 16 (1): 137–157. doi:10.22237/jmasm/1493597280.
  11. Chechik, Gal; Heitz, Geremy; Elidan, Gal; Abbeel, Pieter; Koller, Daphne (2008-06-01). "Max-margin Classification of Data with Absent Features". The Journal of Machine Learning Research. 9: 1–21. ISSN 1532-4435.
  12. Mohan, Karthika; Pearl, Judea (2014). "On the testability of models with missing data". Proceedings of AISTAT-2014, Forthcoming.
  13. Darwiche, Adnan (2009). Modeling and Reasoning with Bayesian Networks. Cambridge University Press.
  14. Potthoff, R.F.; Tudor, G.E.; Pieper, K.S.; Hasselblad, V. (2006). "Can one assess whether missing data are missing at random in medical studies?". Statistical Methods in Medical Research. 15 (3): 213–234. doi:10.1191/0962280206sm448oa.
  15. Pearl, Judea; Mohan, Karthika (2013). Recoverability and Testability of Missing data: Introduction and Summary of Results (PDF) (Technical report). UCLA Computer Science Department, R-417.
  16. Mohan, Karthika; Pearl, Judea; Tian, Jin (2013). Advances in Neural Information Processing Systems 26. pp. 1277–1285.
  17. Mohan, K.; Van den Broeck, G.; Choi, A.; Pearl, J. (2014). "An Efficient Method for Bayesian Network Parameter Learning from Incomplete Data". Presented at Causal Modeling and Machine learning Workshop, ICML-2014.
  18. Mirkes, E.M.; Coats, T.J.; Levesley, J.; Gorban, A.N. (2016). "Handling missing data in large healthcare dataset: A case study of unknown trauma outcomes". Computers in Biology and Medicine. 75: 203–216. arXiv:1604.00627. doi:10.1016/j.compbiomed.2016.06.004. Archived from the original on 2016-08-05.
  • Empty citation (help)

برای مطالعهٔ بیشتر

پیوند به بیرون

پیشینه

نرم‌افزار
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.