زنجیره مارکوف
زنجیرهٔ مارکوف مدلی تصادفی برای توصیف یک توالی از رویدادهای احتمالی است که در آن احتمال هر رویداد فقط به حالت رویداد قبلی بستگی دارد. زنجیرهٔ مارکوف که به افتخار آندری مارکوف ریاضیدان اهل روسیه این گونه نامگذاری شده، یک سیستم ریاضی است که در آن انتقال میان حالات شمارا، از حالتی به حالت دیگر صورت میگیرد. زنجیرهٔ مارکوف یک فرایند تصادفی بدون حافظه است بدین معنی که توزیع احتمال شرطی حالت بعد تنها به حالت فعلی بستگی دارد و مستقل از گذشتهٔ آن است. این نوع بدون حافظه بودن خاصیت مارکوف نام دارد. زنجیرهٔ مارکوف در مدلسازی دنیای واقعی کاربردهای زیادی دارد.
معرفی
زنجیرهٔ مارکوف (Markov Approach modeling) یک فرایند تصادفی گسسته در زمان با خاصیت مارکوف است. اگرچه برخی از نویسندگان در مورد فرایندهای پیوسته در زمان هم از اصطلاح زنجیرهٔ مارکوف استفاده میکنند. یک فرایند تصادفی گسسته در زمان شامل سیستمی است که در هر مرحله در حالت خاص و مشخصی قرار دارد و به صورت تصادفی در هر مرحله تغییر حالت میدهد. مراحل اغلب به عنوان لحظههای زمانی در نظر گرفته میشوند ولی میتوان آنها را فاصله فیزیکی یا هر متغیر گسسته دیگری در نظر گرفت. خاصیت مارکوف بیان میکند که توزیع احتمال شرطی برای سیستم در مرحله بعد فقط به حالت فعلی سیستم بستگی دارد و به حالتهای قبل بستگی ندارد. چون سیستم به صورت تصادفی تغییر میکند بهطور کلی پیشبینی حالت زنجیرهٔد مارکوف در نقطهای خاص در آینده غیرممکن است. با این حال ویژگیهای آماری سیستم در آینده قابل پیشبینی است که در بسیاری از کاربردها همین ویژگیهای آماری بسیار حائز اهمیت است.
تغییرات حالات سیستم انتقال نام دارند و احتمالهایی که به این تغییر حالتها نسبت داده میشوند احتمال انتقال نام دارند. یک فرایند مارکوف با یک فضای حالت شمارا، یک ماتریس گذار برای توصیف احتمالهای هر انتقال و یک حالت اولیه (یا توزیع اولیه) در فضای حالت مشخص میشود. اگر فضای حالت متناهی باشد زنجیر مارکوف را زنجیر مارکوف متناهی یا زنجیر مارکوف با فضای حالت متناهی میگوییم و اگر نامتناهی باشد زنجیر مارکوف را زنجیر مارکوف نامتناهی یا زنجیر مارکوف با فضای حالت نامتناهی میگوییم. طبق قرار داد، فرض میکنیم همیشه حالت بعدی وجود دارد و در نتیجه فرایند تا ابد ادامه پیدا میکند.
یکی از معروفترین زنجیرههای مارکوف که موسوم به «پیادهروی می خواره» است یک پیادهروی تصادفی است که در آن در هر قدم موقعیت با احتمال برابر به اندازه ۱+ یا ۱- تغییر میکند. در هر مکان دو انتقال ممکن وجود دارد یکی به عدد صحیح بعدی(۱+) و یکی به عدد صحیح قبلی(۱-). احتمال هر انتقال فقط به حالت کنونی بستگی دارد. برای مثال احتمال انتقال از ۵ به ۶ برابر با احتمال انتقال از ۵ به ۴ است و هر دوی این احتمالات برابر با ۰٫۵ هستند. این احتمالات مستقل از حالت قبلی (که یا ۴ بوده یا ۶) هستند.
مثالی دیگر عادات غذایی موجودی است که فقط انگور، پنیر و کاهو میخورد و عادات غذایی او از قوانین زیر پیروی میکند:
- او فقط یک بار در روز غذا میخورد.
- اگر امروز پنیر بخورد فردا انگور یا کاهو را با احتمال برابر خواهد خورد.
- اگر امروز انگور بخورد فردا با احتمال ۰٫۱ انگور، با احتمال ۰٫۴ پنیر و با احتمال ۰٫۵ کاهو خواهد خورد.
- اگر امروز کاهو بخورد فردا با احتمال ۰٫۴ انگور و با احتمال ۰٫۶ پنیر خواهد خورد.
عادات غذایی این موجود را میتوان با یک زنجیره مارکوف مدلسازی کرد به دلیل این که چیزی که فردا میخورد (حالت بعدی) تنها به چیزی که امروز خوردهاست (حالت فعلی) بستگی دارد. یکی از ویژگیهای آماری که میتوان در مورد این زنجیره محاسبه کرد امید ریاضی درصد روزهایی است که انگور خوردهاست (در یک دوره طولانی).
مثالهایی از زنجیره مارکوف
ورشکستگی قمارباز
ورشکستگی قمارباز مسئلهای معروف از زنجیره مارکوف است. در این مسئله دو فرد سکه پرتاب میکنند و هر بار که سکه شیر آمد شخص A یک دلار از B میبرد و هر بار سکه خط بیاید، شخص B یک دلار از A میبرد. در ابتدای بازی A مقدار a دلار و B مقدار b دلار دارد. فرض کنید Xi دارایی A پس از i مرحله بازی باشد. یکی از خواص دنباله {Xi} این است که اگر در مرحلهٔ nام مقدار Xi را بدانیم در این صورت سرمایه A از آن مرحله به بعد تنها به Xn و نه به X0, X1, …, Xn-1 وابسته است. یعنی اگر سرمایهٔ A در زمان حال معلوم باشد، سرمایهٔ آیندهٔ او مستقل از پولی است که در هر مرحله از بازی در گذشته برنده شده یا باختهاست.
فرایند زاد مرگ
اگر صد دانه ذرت در فری قرار دهیم، هر دانه در زمانی مستقل که از توزیع نمایی پیروی میکند، منفجر میشود. این مثالی از زنجیره زمان پیوسته مارکوف است. اگر Xt نشاندهنده تعداد دانههای ذرتی باشد که تا زمان t منفجر شدهاند، مسئله را میتوان به صورت تعداد دانههایی که بعد از t منفجر میشوند مطرح نمود. دانستن زمان انفجار دیگر دانهها اهمیتی ندارد و تنها دانستن تعداد دانههایی که تا کنون منفجر شدهاند کافیست. فرایند شرح داده شده در اینجا، تقریبی از یک فرایند پواسونی است. در حالت کلی فرایندهای پواسون نیز فرایند مارکوف هستند.
بازیهای تختهای با تاس
بازی مار و پله یا هر بازی دیگری که حرکات با تاس تعیین میشود یک زنجیرهٔ مارکوف هستند. این نوع بازیها در نقطه مقابل بازیهای کارتی مانند blackjack هستند که کارتها مانند حافظهٔ حرکت قبلی عمل میکنند. برای درک این تفاوتها احتمال یک حرکت مشخص را در بازی در نظر بگیرید. در بالا به بازیهایی که با تاس بازی میشوند اشاره کردیم، تنها چیزی که اهمیت دارد حالت کنونی روی تخته است. حالت بعدی روی تخته به حالت کنونی و چرخش بعدی تاس بستگی دارد و وابسته به اینکه که مهرهها چگونه در حالت کنونی قرار گرفتهاند، نیست. در بازی مانند blackjack، بازیکن میتواند با به خاطر سپردن این که کدام کارتها تاکنون نشان داده شدهاند، برتری کسب کنند؛ بنابراین حالت بعدی بازی مستقل از حالت کنونی نیست.
گامهای تصادفی متمایل به مرکز
یک حرکت تصادفی روی تعدادی خط را در نظر بگیرید، موقعیت کنونی (که x نامیده مینامیم) با احتمالات زیر میتواند به +۱ (به راست) یا -۱(به چپ) تغییر کند:
(c یک عدد ثابت بزرگتر از ۰ است)
به عنوان مثال اگر عدد ثابت c برابر ۱ باشد، احتمال حرکت به چپ از موقعیت x=-۲,-۱٬۰٬۱٬۲ به ترتیب برابرست با:.
یک گام تصادفی یک اثر مرکزی دارد بهطوریکه با افزایش تضعیف c میشود. از آنجایی که احتمالات تنها به وضعیت کنونی بستگی دارد (مقدار x) و وابسته به هیچیک از موقعیتهای قبلی نیست، این گام تصادفی متمایل به مرکز در تعریف زنجیرهٔ مارکوف صدق میکند.
یک مدل آب و هوایی بسیار ساده

احتمال وضعیت آب و هوایی که آب و هوا در طول روز را نشان میدهد و هم به صورت بارانی و هم آفتابی مدل میشود، توسط یک ماتریس انتقال ارائه داده میشود. ماتریس P یک مدل آب و هوایی را نشان میدهد بهطوریکه روز بعد یک روز آفتابی، با احتمال %۹۰ آفتابی است و روز بعد یک روز بارانی، با احتمال %۵۰ آفتابی است. ستونها و سطرها با آفتابی و بارانی برچسبگذاری میشوند.
(P)i j احتمال این است که هوای امروز از نوع i باشد و فردا از نوع j باشد.
در نظر داشته باشید که حاصل جمع احتمالات سطر P برابر ۱ است.
حالت ثابت آب و هوا
در این مثال، پیشبینی هوا در روزهای دور از هم غلط از آب در میآید و متمایل به بردار حالت پایدار است. این بردار احتمال هوای آفتابی و بارانی را در همهٔ روزها نشان میدهد و مستقل از آب وهوای اولیه است.
بردار حالت ثابت به این صورت تعریف میشود:
ولی تنها زمانی به یک مقدار منظم همگراست که p یک ماتریس انتقال منظم باشد (بعبارت دیگر حداکثر یک Pn با ورودیهای غیر صفر وجود دارد)
از آنجایی که q مستقل از شرایط اولیه است، زمانی که بوسیلهٔ P ترجمه میشود، بایستی بدون تغییر بماند؛ که این باعث میشود که q تبدیل به بردار ویژه شود، به این معنی که از P مشتق شود. برای مثال آب و هوا:
پس و از آنجایی که این دو بردار احتمال هستند، داریم
حل این دو معادله یک توزیع حالت یکنواخت را میدهد:
در نتیجه %۸۳ روزها آفتابی است.
تعریف رسمی
زنجیره مارکوف زمان گسسته
یک زنجیره مارکوف دنبالهای از متغیرهای تصادفی X۱،X۲،X۳،... است که دارای خاصیت مارکوف هستند یعنی:
مقادیر ممکن برای Xi مجموعه قابل شمارشی را میسازند که فضای حالت نام دارد.
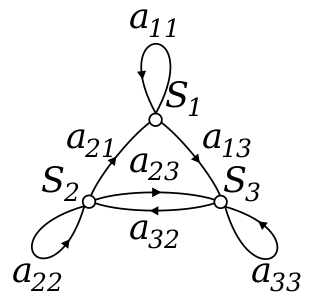
زنجیره مارکوف اغلب توسط دنبالهای از گرافهای جهتدار نشان داده میشود، که در آن یالهای گراف n توسط احتمال از رفتن از یک حالت در زمان n به حالتهای دیگر در زمان n + 1 برچسب گذاری شدهاست. همان اطلاعات در ماتریس انتقال از زمان n به زمان n + 1 درج میشود که در آن عنصر سطر i و ستون j، احتمال تغییر وضعیت از حالت i-1 به حالت j-1 است. مجموع عناصر هر سطر برابر یک است اما الزاماً مجموع عناصر هر ستون یک نمیشود. در نظریه ماتریسها اگر تمام عناصر ماتریسی نامنفی و مجموع عناصر هر سطر یک باشد، در این صورت آن ماتریس را ماتریس مارکوف میگویند. علت آن است که برای چنین ماتریسهایی میتوانیم یک فضای نمونه بسازیم به طوری که عناصر ماتریس، احتمالهای تغیر وضعیت تمام پیشامدهای فضای نمونه باشند و سپس یک زنجیر مارکوف برای فضای نمونه تعریف کنیم. با این حال، زنجیرههای مارکوف اغلب به صورت یکنواخت در زمان فرض میشوند در این صورت گراف و ماتریس مستقل از n هستند و به این ترتیب به شکل یک توالی ارائه نمیشوند.
تعریف دیگری به شرح ذیل عنوان شدهاست: هرگاه فرایند تعمیرات برای سیستمهای تعمیر پذیر لحظهای یا به عبارتی با زمان کوتاه و قابل اغماض در مقایسه با زمان عملکرد سیستم را نتوان مفروض داشت، روشهایی مانند زنجیرهٔ پیوسته مارکوف برای تحلیل سیستم به کار گرفته میشود. روش مارکوف برای مدلسازی رفتار اتفاقی به صورت پیوسته و ناپیوسته نسبت به زمان یا در فضای حالت تقسیمبندی میگردد. این تغییرات پیوسته یا ناپیوسته اتفاقی را اصطلاحاً فرایندهای اتفاقی مینامند. در حقیقت بهکارگیری روش مارکوف نیازمند این امر است که سیستم نماینگر فقدان حافظه باشد. یعنی حالت و وضعیت آیندهٔ سیستم مستقل از وضعیتهای گذشته آن بوده و تنها به آخرین جزء آن وابسته باشد.
زنجیرههای مارکوف یکنواخت در زمان
زنجیرههای مارکوف یکنواخت در زمان، یا ایستا، زنجیرههایی هستند که در آنها:
که رابطه بالا برای هر n صحیح است. در واقع احتمال انتقال مستقل از n است. چنین زنجیرههایی را میتوان تنها با یک ماتریس احتمال انتقال توصیف کرد. ماتریس احتمال انتقال مستقل از زمان n است و درایهٔ (i,j) ام آن، یعنی ، بیانگر احتمال انتقال از حالت i به حالت j میباشد.
زنجیره مارکوف مرتبه m
زنجیره مارکوف مرتبه m (که در آن m متناهی است) فرایندی است که در آن:
به عبارت دیگر حالت بعدی به m حالت قبلی وابستهاست. میتوان یک {Yn} از {Xn} ساخت به طوری که در فرم کلاسیک خاصیت مارکوف صدق کند؛ که در این صورت Y یک چندتایی مرتب از Xها است یعنی:
زنجیره مارکوف افزاینده
یک زنجیره مارکوف افزاینده مرتبه m با رابطه زیر توصیف میشود:
زنجیره مارکوف زمان پیوسته
لامپی را در نظر بگیرید که یا روشن است یا خاموش. اگر لامپ در زمان t روشن باشد X(t) = 1 و اگر خاموش باشد X(t) = 0. در این صورت متغیر تصادفی X زمان گسسته نیست زیرا پس از ورود به حالتی برای یک مدت زمانی که خود نیز متغیری تصادفی است، در آن جا میماند و سپس به حالت دیگری منتقل میشود. این قبیل فرایندها را زنجیره مارکوف زمان پیوسته مینامیم.
یک زنجیره پیوسته مارکف توسط یک فضای حالت متناهی یا شمارا، یک ماتریس نرخ انتقال Q با ابعادی برابر با فضای حالت است. برای i ≠ j، هر عنصر qij غیر منفی است و نرخ انتقال فرایند را از حالت i به حالت j توصیف میکند.
سه تعریف برای فرایندهای مارکوف زمان پیوسته وجود دارد:
تعریف حدی
اگر متغیر تصادفی وضعیت زنجیره درلحظهٔ t با Xt نشان دهیم و فرض کنیم زنجیره در زمان t در حالت i قرار دارد. با توجه به این که Xt = i و Xt+h به مقادیر گذشته وابسته نیستند، هنگامی که h → ۰ برای هر j و t داریم:
که در این معادله دلتای کرونکر است و همچنین از نماد o کوچک استفاده شدهاست. qij میتواند معیاری از سرعت تغییر حالت از i به j باشد.
تعریف زنجیره پرش یا زمان نگهداری
اگر متغیر تصادفی Yn نشاندهندهٔ nامین پرش (تغییر حالت) در زنجیره باشد و متغیرهای زمان ایستایی در هر حالت را نشان دهند، هر کدام از Siها از توزیعی نمایی با پارامتر پیروی میکنند.
تعریف احتمال انتقال
برای هر مقدار و زمانهای با حالتهای داریم:
که در آن pij در دو مجموعه معادلات دیفرانسیلی به نامهای معادلات پیشرو کولموگروف و معادلات پسرو کولموگروف en:Kolmogorov equations صدق میکنند.
تکامل گذرا
احتمال تغییر حالت از حالت iام به حالت jام در n حرکت برابر است با
این احتمال در یک حرکت برابر است با
برای یک زنجیره مارکوف یکنواخت در زمان
و
توجه کنید که برای یک زنجیره مارکوف یکنواخت در زمان، احتمال تغییر حالت از حالت iام به حالت jام در n حرکت معادل است با درایهٔ (i,j) ام ماتریس احتمال انتقال وقتی این ماتریس n بار در خودش ضرب شدهاست:
در حرکتهای n تایی احتمالات بدست آمده برابری چپمن-کولموگروف را ارضا میکنند. پس برای هر k که ۰ <n> k داریم
در این رابطه S فضای حالت زنجیره مارکوف است. توزیع حاشیه ای (Pr(Xn = x مربوط به حرکت nام است. توزیع اولیه برابر است با (Pr(X۰ = x. تعمیم یافته این توزیع برای حرکتهای بعدی به شکل
نمایش داده میشود که در آن n زیروند است و نه توان.
ردهبندی حالتهای یک زنجیر مارکوف
تقلیلپذیری
حالت jام را قابل دسترسی از حالت iام مینامند (i → j) اگر در سیستمی که از حالت iام شروع شود با احتمال غیر ۰ در نهایت به حالت jام برسد. در واقع اگر عدد صحیح n ≥ ۰ وجود داشته باشد که
تساوی n با ۰ به معنای در دسترس بودن همه حالات از حالت iام است. حالت iام را مرتبط با حالت jام مینامند (i ↔ j) اگر هر دو رابطه i → j و j → i برقرار باشند.
مجموعه حالات C را کلاس مرتبط مینامند اگر هر یک از اعضای آن با هر عضو دیگر این مجموعه مرتبط باشد و هیچیک از اعضای C با حالتی که عضو آن نیست مرتبط نباشد. میتوان نشان داد که ارتباط همان همارزی است و کلاسهای مرتبط در واقع کلاسهای همارزی هستند.
یک کلاس همارزی را بسته مینامند اگر احتمال خروج از این کلاس ۰ باشد. به عبارت دیگر اگر حالت i در C باشد و حالت j در C نباشد، j قابل دسترسی از i نیست. مجموعهای از کلاسهای مرتبط یک گراف جهتدار بدون دور را تشکیل میدهند که یالهای آن همان یالهای فضای حالت اصلی هستند. یک کلاس مرتبط بستهاست اگر و تنها اگر هیچ یال خروجی میان کلاسهای مختلف وجود نداشته باشد.
حالت i را ضروری مینامند اگر به ازای همه jهایی که i → j، رابطه j → i نیز برقرار باشد. در غیر این صورت حالت i را غیرضروری مینامند.
اگر تمام وضعیتهای یک زنجیر مارکوف با هم مرتبط باشند، فضای حالت تنها از یک کلاس مرتبط تشکیل میشود و به آن تقلیلناپذیر میگویند. در این زنجیرهها از هر حالت میتوان به هر حالتی رسید.
تناوب
حالت i دارای دوره تناوب k است اگر هر مسیر بازگشت به حالت i به طول مضارب k باشد. به زبان دیگر دوره تناوب یک حالت برابر است با
که در آن gcd بزرگترین مقسوم علیه مشترک است. اگر یک حالت دوره تناوب k داشته باشد ممکن است نتوان به این حالت با k حرکت رسید. بهطور مثال اگر بتوان به حالت i در {۶, ۸, ۱۰, ۱۲, ...} حرکت بازگشت، در این صورت دوره تناوب برابر ۲ خواهد بود حتی اگر ۲ در مقادیر ذکر شده نباشد. اگر k = ۱ باشد، در این صورت به حالت مد نظر غیر متناوب میگویند و بازگشت به حالت i در حرکتهای غیر منظم انجام خواهد گرفت. در غیر این صورت (k > 1)، حالت iدارای دوره تناوب k و متناوب میباشد.
بازگشتپذیری
فرض کنید fi احتمال این پیشامد باشد که زنجیر با شروع از وضعیت i بعد از تعداد متناهی تغییر وضعیت به i برگردد. به وضوح . اگر در این صورت حالت i را بازگشتی یا پایا میگوییم. به این ترتیب هر بار که زنجیر در حالت i قرار میگیرد فرایند بهطور احتمالی حرکت خود را از سر شروع میکند، لذا اولین بازگشت به i مستلزم بازگشت دوم به i، و الی آخر است؛ بنابراین اگر i حالت بازگشتی باشد، فرایند با احتمال ۱ بینهایت بار به i برمیگردد و احتمال اولین بازگشت به این حالت در زمان متناهی برابر ۱ است. اگر امید ریاضی تعداد تغییر وضعیتها تا بازگشت مجدد به i متناهی باشد به i بازگشتی مثبت و در غیر این صورت بازگشتی پوچ میگوییم.[1]
حالت i را گذرا مینامند هرگاه ، به این معنی که اگر سیستم از حالت i شروع به کار کند، احتمال این که دیگر به این حالت بازنگردد غیر صفر است. برای حالت گذرای i احتمال این که فرایند با شروع از i دقیقاً بعد از n بار به آن بازگردد برابر است با. پس تعداد بازگشتها به i متغیر تصادفی با پارامتر میباشد، در نتیجه تعداد بازگشتها بینهایت نمیشود.
با در نظر گرفتن متغیر تصادفی Ti، زمان اولین بازگشت به حالت i، داریم:
عدد احتمال بازگشت سیستم به حالت i برای اولین بار در حرکت nام است. در نتیجه حالت i گذرا است اگر
متوسط زمان بازگشت
اگر زمان اولین بازگشت به حالت i با احتمال ۱ متناهی باشد، نمیتوان نتیجه گرفت که امید ریاضی این زمان متناهی است. امید ریاضی زمان بازگشت به حالت i همان متوسط زمان بازگشت است که از رابطه
محاسبه میشود.
متوسط تعداد بازگشتها
میتوان نشان داد که حالت i پایا است اگر و تنها اگر متوسط تعداد بازگشتها به این حالت نامتناهی باشد. یعنی
چند قضیه مهم[1]
- اگر i گذرا باشد، زنجیره متناهی بار به i بازمیگردد.
- هر زنجیر مارکوف با فضای حالت متناهی حداقل یک حالت بازگشتی دارد
- بازگشتی بودن یک خاصیت ردهای است یعنی اگر i بازگشتی باشد و با j در ارتباط باشد، آنگاه j نیز بازگشتی است.
- گذرا بودن یک خاصیت ردهای است یعنی اگر i گذرا باشد و با j در ارتباط باشد، آنگاه j نیز گذرا است.
- در هر زنجیر مارکوف تقلیلناپذیر یا تمام حالتها گذرا یا تمام آنها بازگشتی هستند. در هر زنجیر مارکوف تقلیلپذیر، عناصر هر رده یا همه گذرا یا همه بازگشتی هستند. در حالت اول رده را رده گذرا و در حالت دوم رده بازگشتی میگوییم.
- هر زنجیر مارکوف تقلیلناپذیر متناهی، بازگشتی است.
- اگر در زنجیره مارکوف با فضای حالت متناهی بازگشتی باشد، در این صورت حتماً بازگشتی مثبت است.
حالتهای مانا
حالت i را جذبکننده یا مانا مینامند اگر با ورود به این حالت خروج از آن غیرممکن باشد. در نتیجه حالت i مانا است اگر و تنها اگر
اگر هر حالت در یک سیستم به حالت مانایی برسد زنجیره مارکوف را زنجیره مارکوف مانا مینامند.
زنجیره ارگودیک و زنجیره باقاعده[2]
یک زنجیره مارکوف ارگودیک است ا اگر بتوان با تعدادی حرکت از هر حالتی به حالت دیگر رسید. زنجیره ارگودیک زنجیره تقلیلناپذیر نیز نامیده میشود. زنجیرهای که هم تقلیلناپذیر باشد و هم غیر متناوب، زنجیره باقاعده (regular) نامیده میشود. به عبارت دیگر زنجیرهای با قاعده است که تقلیلناپذیر باشد و هر حالت آن نامتناوب و بازگشتی مثبت باشد. در زنجیره باقاعده n ای وجود دارد که اگر ماتریس انتقال حالت به توان n برسد تمام درایههای آن مثبت خواهند بود. بدین معنا که با n حرکت میتوان از هر حالتی به حالت دیگر رسید.
متوسط زمان اصابت
در یک زنجیره ارگودیک زمان اولین بار رسیدن یا اصابت به حالت j در حالی که زنجیر مارکوف در حالت i بودهاست، زمان اصابت از i به j نامیده میشود. زمان اصابت با متغیر تصادفی به صورت زیر توصیف میشود:
متوسط زمان اصابت از i به j، یعنی ، از رابطهٔ بازگشتی زیر بدست میآید:
تجزیه و تحلیل توزیع ثابت و محدود کردن توزیعها
برای یک زنجیر یکنواخت در زمان، بردار یک «توزیع ثابت» (یا ایستا) نامیده میشود اگر ها نامنفی و جمع آنها برابر ۱ شود و نیز در رابطه زیر صدق کنند:
یک زنجیره ارگودیک یک توزیع ثابت دارد اگر و فقط اگر همه حالتهای آن مثبت باشند در این صورت π یکتاست و مربوط به زمان بازگشت مورد انتظار است:
اگر زنجیره باقاعده (غیر تقلیل پذیر و غیر متناوب) باشد آن گاه برای هر i و j داریم:
لازم است ذکر شود که هیچ شرطی روی نقطه شروع توزیع وجود ندارد یعنی زنجیره صرف نظر از نقطه شروع به توزیع ثابت میل میکند. این π «توزیع تعادل» زنجیره نامیده میشود. اگر زنجیره بیش از یک کلاس مرتبط بسته داشته باشد توزیع ثابت آن یکتا نخواهد بود. زنجیره غیر یکنواخت در زمان نیز میتواند توزیع تعادل داشته باشد.
در هر صورت اگر حالت j ام غیر متناوب باشد آن گاه:
و برای هر حالت i دیگر اگر fij احتمال این باشد که زنجیره در حالت j قرار گیرد در صورتی که شروع زنجیره از حالت i باشد خواهیم داشت:
اگر حالت i متناوب باشد با دوره تناوب k > 1 آنگاه حد
وجود ندارد و نیز حد
برای هر r صحیح وجود ندارد.
زنجیره وارون پذیر
یک زنجیره مارکوف وارون پذیر نامیده میشود اگر یک توزیع احتمال بر روی حالتها وجود داشته باشد بهطوریکه برای تمام زمانهای n و حالتهای i و j رابطهٔ زیر برقرار باشد:
برای زنجیرههای یکنواخت در زمان رابطهٔ بالا به صورت سادهٔ زیر نوشته میشود:
توزیع احتمال در رابطهٔ بالا همان توزیع ثابت در زنجیرههای ارگودیک میباشد.
کاربردها
فیزیک
سیستمهای مارکوفی در ترمودینامیک و مکانیک آماری بسیار ظاهر میشوند، جایی که احتمال برای نشان دادن ویژگیهای ناشناخته سیستم به کار میرود، اگر بتوان فرض کرد که دینامیک مستقل از زمان است و احتیاجی به بررسی پیشینه تاریخی آن نیست. مسیرها، در فرمول انتگرال مسیر مکانیک کوانتومی، زنجیره مارکوف هستند. همچنین زنجیر مارکوف در شبیهسازی شبکهای QCD استفاده میشود.
علم اطلاعات
زنجیره مارکوف در نظریه اطلاعات کاربرد دارد. مقاله معروف کلود شانون در سال ۱۹۴۸ با «نظریه ریاضی ارتباطات» که پایهگذار نظریه اطلاعات شد با معرفی آنتروپی از طریق مدلسازی مارکوف از زبان انگلیسی آغاز میشود. چنین مدلهای ایدهآلی بسیاری از قواعد آماری سیستم را به دست میدهند. حتی بدون داشتن ساختار کامل سیستم این گونه مدلسازیها فشرده سازی مؤثر دادهها را ممکن میسازند.
زنجیرههای مارکوف پایه و اساس مدل پنهان مارکوف است که این مدل یکی از ابزارهای مهم در زمینههای گوناگون مثل شبکههای تلفن (برای تصحیح خطا)، تشخیص گفتار و هم چنین بیوانفورماتیک است.
نظریه صف
زنجیرههای مارکوف اساس رفتار تحلیلی صف ها(نظریه صف) میباشد و این امر وجود آنها را برای بهینهسازی عملکرد شبکههای مخابراتی حیاتی میسازد. جایی که پیامها برای منابع محدود (مانند پهنای باند) رقابت میکنند. مدلهای صف بندی بسیاری از زنجیره مارکوف زمان پیوسته استفاده میکنند. برای مثال، یک صف M / M / 1 یک CTMC بر روی عدد صحیح غیر منفی است که در آن انتقال از i به i + 1 بر اساس یک فرایند پوآسون با نرخ λ رخ میدهد و ورود کار را توصیف میکند، در حالی که انتقال از i به i - 1 (برای i> 1) در نرخ μ اتفاق میافتد (بار خدمات شغلی از توزیع نمایی پیروی میکنند) و خدمات کامل یا همان خروج از صف را نشان میدهد.

کاربرد اینترنتی
یکی از نتایج جالب از زنجیرهٔ مارکوف این است که با افزایش طول زنجیر (افزایش تعداد تغییر حالات)، احتمال رسیدن به یک حالت خاص به عددی ثابت همگرا خواهد شد. اکنون تمام شبکه جهانی وب را یک زنجیره مارکوف در نظر بگیرید که در آن هر صفحه یک حالت و پیوند میان آنان احتمال هر تغییر حالت را مشخص میکند. این نظریه میگوید مستقل از صفحهای که از آن شروع کردهایم، پس از مدتی طولانی گشتن در وب احتمال رسیدن به صفحهای خاص مقدار ثابتی دارد. با این مدلسازی میتوان گفت هر چه احتمال رسیدن به یک صفحه بیشتر باشد، آن صفحه از اهمیت بالاتری برخوردار است.[3]
رتبه صفحه (Page Rank)، برای یک صفحهٔ وب که گوگل نیز از آن استفاده کردهاست، توسط یک زنجیره مارکوف تعریف شدهاست. همچنین مدل مارکوف برای تحلیل رفتارهای وب کاربران و سیر حرکت آنها میان صفحات استفاده شدهاست. انتقال کاربر به یک صفحه وب خاص از طریق یک لینک میتواند با استفاده از مدلهای مارکوف مرتبه اول یا دوم مدل شود و برای پیشبینیهای مربوط به حرکات آینده و شخصیسازی وب برای کاربر مورد استفاده قرار گیرد.
منابع
- Saeed Gahramani, Fundamentals of Probability, whit stochastic processes (3rd edition)
- Grinstead, Charles Miller, and James Laurie Snell, eds. Introduction to probability. American Mathematical Soc. , 1997.
- «What Are Markov Chains? 5 Nifty Real World Uses». MakeUseOf (به انگلیسی). دریافتشده در ۲۰۱۸-۱۲-۲۷.
- مشارکتکنندگان ویکیپدیا. «Markov chain». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۶ ژوئیهٔ ۲۰۱۲.