مدل واسیچک

در ریاضیات مالی، مدل واسیچک(به انگلیسی: vasicek model) یک مدل ریاضی برای توصیف تکامل نرخ بهره است. این نوع از مدل، نرخ کوتاه مدت تک عاملی است که تغییرات نرخ بهره را با توجه به یک نوع از ریسک بازار توصیف می‌کند. این مدل می‌تواند در ارزیابی نرخ بهره اوراق مشتقه استفاده شود؛ و نیز با بازارهای اعتباری تطابق داده‌ شده‌است، گرچه استفاده از آن در بازارهای اعتباری اشتباه است و به احتمالات منفی اشاره می‌کند. اما آن در سال ۱۹۷۷ توسط 《Oldřich Vašíček 》معروف شد[1] و توانست به عنوان مدل سرمایه‌گذاری شناخته شود.

A trajectory of the short rate and the corresponding yield curves at T=0 (purple) and two later points in time

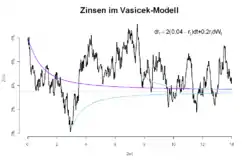
جزئیات

این مدل نشان می‌دهد که نرخ بهره آنی پیرو معادله دیفرانسیل تصادفی می‌باشد.

${\displaystyle dr_{t}=a(b-r_{t})\,dt+\sigma \,dW_{t}}$

که wt فرایند وینر تحت ریسک مستقل از چارچوب مدل سازی در عامل ریسک بازار به صورت تصادفی است، چرا که جریان مستمر اعداد تصادفی در سیستم را مدل‌سازی می‌کند. پارامتر انحراف استاندارد σ، نوسانات نرخ بهره را تعیین می‌کند و تا اندازه‌ای نوسانات جریان تصادفی آنی را مشخص می‌کند. پارامترهای نوع a ،b وσ همراه با شرایط اولیه ro، به‌طور کامل دینامیک را مشخص می‌کند، و با غیرمنفی فرض کردن a، به صورت زیر مشخص می‌شود b :"میانگین میزان بلند مدت": تمام منحنی‌های بعدی r پیرامون میانگین میزان b در درازمدت خواهد بود. a:" سرعت بازگشت":a سرعتی را مشخص می‌کند که در آن منحنی‌ها پیرامون b جمع می‌گردند. σ: "نوسانات آنی (لحظه‌ای)"، دامنهٔ اعداد تصادفی ورودی به سیستم را لحظه به لحظه اندازه‌گیری می‌کند. هر چه σ بیشتر باشد اعداد تصادفی بیشتر خواهد بود. مقدار مشتق شدهٔ زیر نیز مورد توجه است

• ${\displaystyle {\sigma ^{2}}/(2a)}$: واریانس بلند مدت: تمام منحنی‌های بعدیِ r اطراف میانگین بلند مدت با چنین واریانسی در طول زمان جمع خواهند شد.

aوσ مخالف یکدیگرند: افزایش σ، میزان اعداد تصادفی ورودی به سیستم را افزایش می‌دهد، اما در عین حال افزایش a باعث افزایش سرعت می‌شود که در آن سیستم به صورت آماری در میانگین بلند مدت با واریانسِ تعیین شده توسط a، ثابت خواهد شد؛ که با مشاهدهٔ واریانس بلند مدت این موضوع روشن خواهد شد.

${\displaystyle {\frac {\sigma ^{2}}{2a}}}$

که در آن افزایش با σ، وکاهش با a می‌باشد. این یک مدل فرایند تصادفی از Ornstein–Uhlenbeck است. ایجاد میانگین تصادفی در SDE، یک نسخهٔ ساده شده از cointelation SDE است[2].

بحث

اولین مدلی که بازگشت به میانگین را تسخیر می‌کند مدل vasicek بود. یکی از ویژگی‌های اساسی نرخ بهره جدا بودن مجموعه آن از سایر قیمت‌های مالی است؛ بنابراین بر خلاف قیمت‌های سهام که می‌تواند به‌طور نامحدود افزایش یابند، نرخ‌های بهره به‌طور نامحدود نمی‌توانند افزایش یابد. به خاطر این است که سطح بالای آن مانع فعالیت‌های اقتصادی و باعث کاهش نرخ بهره می‌شود. مثلاً نرخ‌های بهره معمولاً نمی‌توانند کمتر از صفر شوند. در نتیجه تغییرات نرخ‌های بهره دردامنه محدود، تمایل به بازگشت ارزش بلند مدت را نشان می‌دهد. عامل انحراف ${\displaystyle a(b-r_{t})}$ نشان دهنده انتظار تغییرات آنی درنرخ بهره در زمانt. پارامتر b بازگشت نرخ بهره به سمت ارزش تعادلی بلندمدت را نشان می‌دهد. در واقع در صورت عدم وجود شوک(${\displaystyle dW_{t}=0}$)، نرخ بهره ثابت باقی می‌ماند زمانی که rt = b. پارامتر a، نماینده سرعت تعدیل، باید مثبت باشد تا ثبات در ارزش بلند مدت را تضمین کند، برای مثال وقتی rt کمتراز b است، بخش انحراف ${\displaystyle a(b-r_{t})}$ مثبت می‌شود به خاطر مثبت بودن a، ایجاد یک تمایل تغییرات نرخ بهره رو به بالا (به سمت بالا) ضعف اصلی این است که، تحت مدل vasicek، از لحاظ نظری ممکن است نرخ بهره برای تبدیل شدن به منفی، یک ویژگی نامطلوب تحت مفرضات قبل از بحران باشد. این کمبود در مدل Cox–Ingersoll–Ross model، مدل Vasicek نمایی، مدل Black–Derman–Toy model و مدل Black–Karasinski model، در میان بسیاری دیگر ثابت شد. مدل vasicek بیشتر تعمیم داده شده در مدل Hull–White model. مدل vasicek همچنین یک مدل متعارف از مدل affine term structure model، همراه با مدل Cox–Ingersoll–Ross model است.

میانگین و واریانس تقریبی

برای بدست آوردن معادله دیفرانسیل تصادفی باید فرمول زیر را حل کنیم.

${\displaystyle r(t)=r(0)e^{-at}+b\left(1-e^{-at}\right)+\sigma e^{-at}\int _{0}^{t}e^{as}\,dW_{s}.\,\!}$

با استفاده از تکنینک‌های مشابه به عنوان مثال با اعمال فرایند تصادفی Ornstein–Uhlenbeck ما در می‌یابیم که متغیر حالت با میانگین و واریانس نرمالی توزیع شده‌است. میانگین

${\displaystyle \mathrm {E} [r_{t}]=r_{0}e^{-at}+b(1-e^{-at})}$

واریانس

${\displaystyle \mathrm {Var} [r_{t}]={\frac {\sigma ^{2}}{2a}}(1-e^{-2at}).}$

و به تبع آن ما داریم،

${\displaystyle \lim _{t\to \infty }\mathrm {E} [r_{t}]=b}$

و

${\displaystyle \lim _{t\to \infty }\mathrm {Var} [r_{t}]={\frac {\sigma ^{2}}{2a}}.}$

منابع

1. Vasicek, O. (1977), "An equilibrium characterization of the term structure", J.Financial Economics, 5: 177–188
2. Mahdavi Damghani B. (2013). "The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model". Wilmott Magazine. doi:10.1002/wilm.10252.

• Hull, John C. (2003). Options, Futures and Other Derivatives. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-009056-5.
• Vasicek, Oldrich (1977). "An Equilibrium Characterisation of the Term Structure". Journal of Financial Economics. 5 (۲): 177–188. doi:10.1016/0304-405X(77)90016-2.
• Damiano Brigo, Fabio Mercurio (2001). Interest Rate Models – Theory and Practice with Smile, Inflation and Credit (2nd ed. 2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4.
• Jessica James, Nick Webber (2000). Interest Rate Modelling. Wiley. ISBN 0-471-97523-0.

پیوند به بیرون

• Price of Zero Coupon Bond under Vasicek Model, Free Online Calculator, QuantCalc
• The Vasicek Model, Bjørn Eraker, Wisconsin School of Business
• Yield Curve Estimation and Prediction with the Vasicek Model, D. Bayazit, دانشگاه خاورمیانه