دور (نظریه گراف)

در نظریه گراف، دور (به انگلیسی: Cycle) گرافی است که تعداد برابری از یال و رأس دارد، به‌طوری‌که رئوس می‌توانند روی یک دایره قرار بگیرند و هر دو رأس این گراف مجاورند، اگر و تنها اگر روی دایرۀ به‌صورت متوالی قرار گرفته باشند. به‌عبارت دقیق‌تر، در یک گراف با مجموعه رئوس V و مجموعه یال‌های E، یک دور عبارت است از دنباله‌ای به‌شکل ${\displaystyle v_{0},e_{1},v_{1},\ldots ,v_{n-1},e_{n},v_{n}}$ (${\displaystyle v_{i}\in V,0\leqslant i\leqslant n}$ و ${\displaystyle e_{j}\in E,0<j\leqslant n}$) که ${\displaystyle v_{0}=v_{n}}$ و به‌جز این دورِ رأس در دنباله همۀ رئوس و همۀ یال‌ها غیرتکراری باشند.

گراف با یال‌های رنگ‌آمیزی شده. H-A-B مسیر، B-D-E-F-D-C-B پیمایش و H-D-G-H دور می‌باشد.

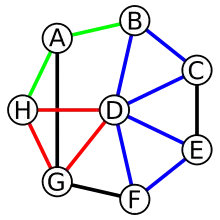
تشخیص دور

پیدا کردن دور یا تشخیص وجود آن در گراف بدونِ جهت و گراف جهت‌دار به وسیله جستجوی عمق اول امکان‌پذیر است. یال برگشت (به انگلیسی: Back Edge) به یالی مانند e گفته می‌شود که از رأس u - که در مرحله کنونی اجرای الگوریتم در آن مشغول جستجو هستیم - به رأسی مانند v باشد، در حالی‌که که v یکی از اجداد u است. حال اگر جستجوی عمقِ اوّل در حین اجراء به یک یال برگشت و برخورد، نشان‌دهندۀ این است که گراف شامل حداقّل یک دور است. در صورتی هم که هیچ یال برگشتی وجود نداشته باشد، گراف فاقد دور است. در گراف هم‌بند بدون جهت با مجموعۀ رئوس V زمانِ اجرای این الگوریتم برای پیدا کردن دور از ${\displaystyle O(|V|)}$ است زیرا حداکثر ${\displaystyle |V|-1}$ یال از این گراف می‌توانند متعلق به یک درخت باشند و اگر بیش از این تعداد یال وجود داشته باشد، گراف دور دارد.

مراحل پیدا کردن دور در گراف ساده به‌وسیلۀ الگوریتم جستجوی عمق اوّل

روشِ دیگر برای تشخیص دور در گرافِ ساده استفاده از داده‌ساختار مجموعه‌های مجزا یا همان داده‌ساختار ادغام-جستجو (به انگلیسی: Union-Find) است که به اِزای هر یال e که بین دو راس u و v قرار گرفته‌است، اگر نتیجهٔ جستجو u و v یکسان بود؛ یعنی از قبل در مؤلفه یکسانی بودند و e یک دور ایجاد خواهد کرد و دور پیدا شده‌ است، در غیر این صورت مؤلفه دو رأس را با هم ادغام می‌کنیم.[1]

دور منفی

گرافی که شامل ۳ دور است. دور a-b-e-f-a و دور a-b-c-d-e-f-a منفی هستند. دور b-c-d-e-b مثبت است.

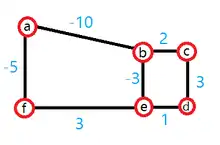
همچنین، در گراف وزن‌دار دور منفی به دوری گفته می‌شود که مجموع وزن یال‌های تشکیل‌دهندهٔ آن عددی منفی شود. وجود دور منفی اهمیّت زیادی در مسائل یافتن کوتاهترین مسیر دارد زیرا اگر در گراف وزن‌داری دور منفی وجود داشته باشد، می‌توان هزینۀ رسیدن از رأسی به رأس دیگر را با انجام یک پیمایش (به انگلیسی: Walk) بیشتر کاهش داد. در چنین حالتی، پیدا کردن جواب مسئله کوتاه‌ترین مسیر در زمان چندجمله‌ایی راه حلی ندارد. دلیل آن هم این است که می‌توان به هر یالِ یک گراف G، وزن ۱- نسبت داد و گراف 'G را به دست آورد که در این صورت پیدا کردن کوتاه‌ترین مسیر در گراف 'G (که ممکن است دور منفی داشته باشد) هم‌ارز پیدا کردن طولانی‌ترین مسیر در گراف G است و می‌دانیم که پیدا کردن طولانی‌ترین مسیر یک مسئله NP-Hard است. در نتیجه، مسئلهٔ پیدا کردن کوتاه‌ترین مسیر در گرافی با دورِ منفی راه‌حلّ چندجمله‌ایی ندارد، مگر آن‌که ثابت شود. (P=NP)

با توجه به مشکلاتی که وجود دور منفی را برای پیدا کردن کوتاه‌ترین مسیر در گراف ایجاد می‌کند، برخی از الگوریتم‌های این مسئله مانند الگوریتم بلمن-فورد یا الگوریتم فلوید-وارشال می‌توانند وجود دور منفی در گراف را تشخیص دهند.

هم‌چنین، در برخی از کاربردها، وجود یک دور منفی معادلِ وجود یک بن‌بست (به انگلیسی: Deadlock) در سیستم است که تشخیص وجود آن اهمیّت دارد.

منابع

1. http://www.geeksforgeeks.org/union-find/

• B.West, Douglas (2002). "Fundamental Concepts". Introduction to Graph Theory. Pearson Education. ISBN 81-7808-830-4.
• http://cstheory.stackexchange.com/questions/17462/finding-the-shortest-path-in-the-presence-of-negative-cycles
• https://en.wikipedia.org/wiki/Floyd–Warshall_algorithm
• https://en.wikipedia.org/wiki/Bellman–Ford_algorithm