رشد دانه
در علم مواد، رشد دانه افزایش اندازه دانهها (کریستالیتها) در یک ماده با دمای بالا میباشد. این امر زمانی اتفاق میافتد که بازیابی و تبلور مجدد کامل شده باشد و کاهش بیشتر انرژی داخلی فقط با کاهش سطح کل مرز دانه حاصل شود. این اصطلاح معمولاً در متالورژی مورد استفاده قرار میگیرد اما از آن در سرامیک و مواد معدنی نیز استفاده میشود.
اهمیت رشد دانه
بیشتر مواد اثرات هال پچ را در دمای اتاق نشان میدهند و بنابراین وقتی اندازه دانه کاهش مییابد تنش تسلیم بیشتری نشان میدهد. در دماهای بالا برعکس آن صادق است از آنجایی که طبیعت باز و بی نظم مرزهای دانه به معنای این است که تهی جایی میتواند با سرعت بیشتری در مرزها پراکنده شود که منجر به Coble creep سریعتری میشود. از آنجا که مرزها مناطقی با انرژی بالا هستند، آنها مکانهای مناسبی برای هسته رسوبات و سایر فازهای ثانویه هستند به عنوان مثال فازهای منیزیم-سیلیکون - مس در برخی از آلیاژهای آلومینیوم یا پلاکتهای مارتنزیت در فولاد. بسته به فاز ثانویه مورد نظر، این ممکن است اثرات مثبت یا منفی داشته باشد.
قوانین رشد دانه
رشد دانه عمدتاً برای مدت طولانی با بررسی نمونههای برش خورده، صیقلی و سونش شده در زیر میکروسکوپ نوری مورد مطالعه قرار گرفتهاست. اگرچه چنین روشهایی امکان جمعآوری تعداد زیادی از شواهد تجربی را فراهم میآورد، به ویژه با توجه به عواملی مانند دما یا ترکیب، کمبود اطلاعات کریستالیوگرافی باعث محدود شدن افزایش درک درستی از فیزیک بنیادی میشود. با این وجود، موارد زیر از رشد دانه به خوبی تثبیت شدهاند:
- رشد دانه با حرکت مرزهای دانه رخ میدهد، نه با همبستگی (مثل قطرات آب)
- حرکت مرزی ناپیوسته است و ممکن است جهت حرکت ناگهان تغییر کند.
- ممکن است یک دانه به یک دانه دیگر تبدیل شود در حالی که از طرف دیگر مصرف میشود
- هنگامی که دانه تقریباً مصرف شدهاست، نرخ مصرف آن بیشتر میشود
- یک مرز منحنی شکل بهطور معمول به سمت مرکز انحنای خود حرکت میکند
- هنگامی که مرزهای دانه در یک فاز واحد با هم زاویههایی به غیر از ۱۲۰ درجه بسازند، دانه شامل زاویه حاد تر مصرف میشود به طوری که زاویهها به ۱۲۰ درجه نزدیک میشوند.
نیروی محرکه
مرز بین یک دانه و همسایه آن (مرز دانه) نقصی در ساختار بلوری است و بنابراین با مقدار مشخصی از انرژی همراه است. در نتیجه، یک نیروی محرک ترمودینامیکی برای مساحت کل مرز وجود دارد که تمایل دارد مساحت را کاهش دهد. با افزایش اندازه دانه و کاهش تعداد واقعی دانه در حجم، سطح کل مرز دانه کاهش مییابد.
سرعت محلی یک مرز دانه در هر نقطه با انحنای موضعی مرز دانه متناسب است، یعنی:
،
سرعت مرز دانه ، تحرک مرز دانه (در حالت کلی به جهتگیری دو دانه بستگی دارد) ، انرژی مرز دانه و جمع دو منحنی سطح اصلی است. برای مثال سرعت کوچک شدن یک دانه کروی که در دانه دیگری محاط شدهاست برابر است با:
،
شعاع کره است. این فشار محرکه در طبیعت بسیار مشابه فشار لاپلاس است که در کفها به وجود میآید.
در مقایسه با دگرگونیهای فازی، انرژی موجود برای رشد دانه بسیار کم است و بنابراین در سرعتهای بسیار کندتر رخ میدهد و به راحتی با حضور ذرات فاز ثانویه یا اتمهای حل شونده در ساختار کاهش مییابد.
رشد ایدهآل دانه
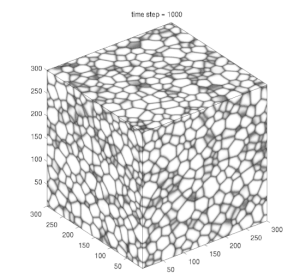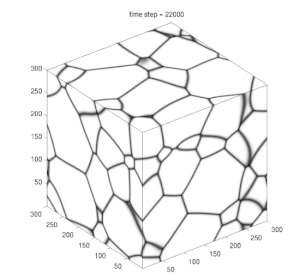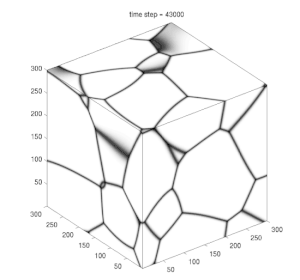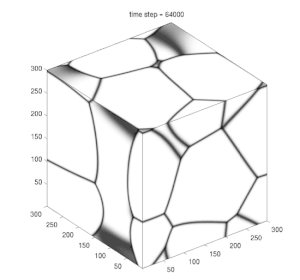
رشد ایدهآل دانه یک مورد خاص از رشد معمولی دانه است که حرکت مرزی فقط توسط انحنای محلی مرز دانه حرکت داده میشود. این امر باعث کاهش مقدار کل سطح مرزی دانه یعنی انرژی کل سیستم میشود. همکاریهای اضافه به نیروی محرکه مانند کرنشهای الاستیک یا گرادیان دما صرف نظر میشوند. اگر در نظر بگیریم که سرعت رشد متناسب با نیروی محرکه است و نیروی محرک متناسب با مقدار کل انرژی مرزی دانه است، میتوان نشان داد که مدت زمان t برای رسیدن به اندازه دانه معین با معادله زیر تقریب زده میشود
d 0 اندازه اولیه دانه است، d اندازه نهایی دانه و k یک ثابت وابسته به دما است که توسط یک قانون نمایی محاسبه میشود:
که k 0 یک ثابت است، T دمای مطلق و Q انرژی فعال سازی برای تحرک مرز است. از لحاظ تئوری، انرژی فعال سازی برای تحرک مرزی باید برابر با خود پراکندگی باشد اما معمولاً اینگونه نیست.
بهطور کلی این معادلات برای مواد با خلوص فوقالعاده بالا صدق میکنند اما وقتی حتی غلظتهای کوچک حل شونده در نظر گرفته شود صحت این معادلات به سرعت از بین میرود.
خود تشابهی

یک موضوع قدیمی در رشد دانه ، تکامل توزیع اندازه دانه است. با الهام از کار لیفشیتز و اسلیوزو در عمل آمدن استوالد، هیلرت پیشنهاد کردهاست که در یک فرایند رشد دانه طبیعی تابع توزیع اندازه باید به یک راه حل خود مشابه همگرا شود، یعنی آن نامتغیر میشود هنگامی که اندازه دانه با طول مشخصه کوچک سیستم مدرج شود که متناسب است با اندازه متوسط دانه .
با این وجود چندین مطالعهات شبیهسازی شده نشان دادهاند که توزیع اندازه از راه حل خود متشابه هیلرت منحرف میشود.[2] از این رو جستجوی راه حل خود متشابه جدید امکانپذیر آغاز شد که در واقع به به وجود آمدن کلاس جدیدی از توابع توزیع متشابه به خود منجر شد.[3][4][5] شبیهسازی میدان-فاز در مقیاس بزرگ نشان دادهاست که واقعاً یک رفتار خود متشابه در توابع توزیع جدید امکانپذیر است. نشان داده شدهاست که منشأ انحراف از توزیع هیلرت در واقع هندسه دانهها به خصوص هنگام کوچک شدن است.[6]
عادی درمقابل غیرعادی
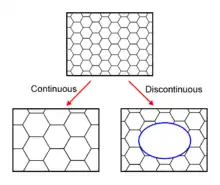
با بهبود و تبلور مجدد، پدیدههای رشد را میتوان در مکانیسمهای پیوسته و ناپیوسته تفکیک کرد. در گذشته، ساختار از حالت A تا B (در این مورد دانهها بزرگتر میشود) به شکلی یکنواخت تکامل مییابد. در حالت دوم، تغییرات بصورت ناهمگن اتفاق میافتد و ممکن است مناطق تغییر شکل یافته و تغییر شکل نیافته خاص ممکن است وجود داشته باشند. رشد غیرطبیعی یا ناپیوسته دانه با زیر مجموعه ای از دانههایی شناخته میشوند که با سرعت بالا رشد مییابند و با از بین بردن همسایگانشان به وجود میآیند و اینکه تمایل به تولید ریزساختاری تحت سلطه چند دانه بسیار بزرگ دارد. برای رسیدن به این امر، زیر مجموعه دانهها باید نسبت به رقبای خود دارای مزیتهایی باشند از جمله انرژی مرز دانه بالا، تحرک محلی مرز دانه بالابه میزان، بافت مطلوب یا تراکم ذرات فاز دوم محلی پایینتر.[7]
عواملی که مانع رشد هستند
در صورت وجود عوامل اضافی که مانع از حرکت مرزی میشوند، مانند زنر پینینگ توسط ذرات، اندازه دانه ممکن است به مقدار بسیار پایینتر از آنچه انتظار میرود محدود شود. این یک مکانیسم مهم صنعتی در جلوگیری از نرم شدن مواد در دمای بالا است.
بازداری
برخی مواد به ویژه مواد نسوز که در دمای بالا فرآوری میشوند، دارای اندازه دانه بسیار بزرگ و خواص مکانیکی ضعیف در دمای اتاق هستند. برای کاهش این مشکل در یک روش مشترکتفجوشی، انواع گوناگونی از ناخالصیها برای مهار رشد دانه استفاده میشوند.
منابع
- F. J. Humphreys and M. Hatherly (1995); Recrystallization and related annealing phenomena, Elsevier
- Darvishi Kamachali, Reza (2013). "Grain boundary motion in polycrystalline materials, PhD thesis" (PDF). Archived from the original (PDF) on 25 October 2018.
- Acta Materialia 60 (2012). "3-D phase-field simulation of grain growth: Topological analysis versus mean-field approximations".
- Brown, L.C. (1992-06-15). "Answer to the rebuttal of Hillert, Hunderi and Ryum". Scripta Metallurgica et Materialia. 26 (12): 1945. doi:10.1016/0956-716X(92)90065-M. ISSN 0956-716X.
- Coughlan, S.D.; Fortes, M.A. (1993-06-15). "Self similar size distributions in particle coarsening". Scripta Metallurgica et Materialia. 28 (12): 1471–1476. doi:10.1016/0956-716X(93)90577-F. ISSN 0956-716X.
- Rios, P.R (1999-02-19). "Comparison between a computer simulated and an analytical grain size distribution". Scripta Materialia. 40 (6): 665–668. doi:10.1016/S1359-6462(98)00495-3. ISSN 1359-6462.
- Acta Materialia 90 (2015). "Geometrical grounds of mean field solutions for normal grain growth".
- Hanaor, D.A.H; Xu, W; Ferry, M; Sorrell, CC (2012). "Abnormal grain growth of rutile TiO2 induced by ZrSiO4". Journal of Crystal Growth. 359: 83–91. arXiv:1303.2761. doi:10.1016/j.jcrysgro.2012.08.015.