رنگ آمیزی آزمند

الگوریتم رنگ آمیزی آزمند (حریصانه) (به انگلیسی: Greedy coloring) در میان مسائل گوناگون رنگ آمیزی گراف، یک الگوریتم آزمند برای رنگ آمیزی رئوس یک گراف می‌باشد. این روش رئوس گراف را بر اساس ترتیب مشخصی انتخاب کرده و تلاش می‌کند با رنگ‌هایی که در رنگ آمیزی رئوس قبلی به کار رفته آن را به گونه‌ای رنگ کند که هیچ دو راس مجاوری دارای رنگ یکسان نباشند. در صورتی‌که امکان استفاده از رنگ‌های پیشین نباشد یک رنگ جدید به مجموعه رنگ‌ها اضافه می‌شود. اگرچه با استفاده از این الگوریتم در همه حالات جواب بهینه برای مسائل رنگ آمیزی بدست نخواهد آمد اما به‌طور کلی از آن برای کمینه کردن تعداد رنگ‌های لازم برای رنگ آمیزی گراف استفاده می‌شود.
این الگوریتم از دو قسمت اصلی تشکیل شده‌است: مرتب‌سازی رئوس و مرتب‌سازی رنگ‌ها

مرتب‌سازی رئوس

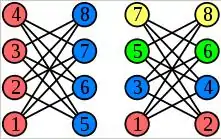
معمولاً الگوریتم رنگ آمیزی آزمند، بدترین عملکرد خود را بر روی گراف‌های کامل دوبخشی k n,n دارد که یال نظیر رئوس xi و xj که i=j حذف شده‌اند.

در صورتی‌که پس از شماره‌گذاری رئوس، دو راسی که در یک یال حذف شده قرار دارند به صورت متوالی شماره‌گذاری شوند، چنین گرافی با n رنگ، رنگ آمیزی می‌شود درحالیکه یک گراف ۲-رنگ پذیر است؛ بنابراین ترتیب رئوس در الگوریتم آزمند اهمیت فراوانی دارد.

دو الگوریتم آزمند با ترتیب رئوس متفاوت بر روی یک گراف

یکی از روش‌های معمول شماره‌گذاری رئوس، انتساب کمترین اولویت به راس با کمترین درجه و مرتب‌سازی بقیه رئوس به همین شکل است. اگر هر زیرگراف یک گراف دارای بیشینه درجه d باشد الگوریتم حریصانه حداکثر از d+۱ رنگ استفاده می‌کند.

برای گرافی با بیشینه درجه D الگوریتم حریصانه از حداکثر D+۱ رنگ استفاده می‌کند. قضیه بروک[1] نشان می‌دهد این تعداد با دو استثنا (گراف‌های cliques, odd cycle) حداکثر برابر D است. یکی از روش‌های اثبات این نظریه، شماره‌گذاری رئوس به صورتیست که دو راس اول، مجاور راس نهایی بوده ولی با یکدیگر مجاور نباشند بنابراین تعداد رنگ‌های استفاده شده الگوریتم آزمند برابر D خواهد بود. پاسخ به این سؤال که آیا برای گراف مفروض G وعدد مفروض K یک الگوریتم آزمند وجود دارد که گراف را با کمتر از K رنگ، رنگ آمیزی کند یا خیر یک مسئله NP-Complete است.

تعدادی از معروف‌ترین الگوریتم‌های شماره‌گذاری رئوس عبارتند از:

ترتیب خاص از پیش تعیین شده (SPECIFIC-PREDEFINED-ORDERING:SP)

ترتیب کاهش درجه نودها (DECREASING DEGREE ORDERING: DD) به عبارت دیگر هر بار راس رنگ نشده با بزرگترین درجه

ترتیب افزایش درجه نودها(INCREASING DEGREE ORDERING: ID) به عبارت دیگر هر بار راس رنگ نشده با کوچکترین درجه

ترتیب درجه اشباع نودها (SATURATION DEGREE ORDERING:SD) که درجه اشباع یک نود عبارتست از تعداد رنگ‌های به کار رفته در رنگ آمیزی نودهای مجاورش

مرتب‌سازی رنگ‌ها

در الگوریتم رنگ آمیزی حریصانه همیشه اولین رنگ در دسترس را به راس انتخاب شده اختصاص نمی‌دهیم. همان‌طور که مرتب‌سازی رئوس در نتجه عملیات تأثیرگذار است، شیوه انتخاب رنگ‌ها نیز مؤثر خواهد بود.

از معروف‌ترین الگوریتم‌های حریصانه مرتب‌سازی رنگ‌ها عبارتند از:

SIMPLE-SEARCH-GREEDY:SSG: این روش کلاس‌های رنگ را بر اساس یک ترتیب از پیش تعریف شده انتخاب می‌کند.

LARGEST-FIRST-SEARCH-GREEDY:LFSG: کلاس‌های رنگ را بر اساس سایزشان (تعداد نودهای موجود در هر یک) به ترتیب نزولی مرتب کرده از بینشان انتخاب می‌کند؛ بنابراین، این روش متمایل به ایجاد کلاس‌های رنگ با بزرگترین سایز است.

SMALLEST-FIRST-SEARCH-GREEDY:SFSG: کلاس‌های رنگ را بر اساس سایز آن‌ها به ترتیب صعودی مرتب می‌کند؛ بنابراین این روش متمایل به تراز کردن و توزیع یکنواخت نودها در بین کلاس‌های رنگ می‌باشد.

هر یک از متدهای مرتب‌سازی آزمند رنگ‌ها در ترکیب با روش‌های مختلف مرتب‌سازی نودها، یک الگوریتم کامل آزمند برای رنگ آمیزی گراف ایجاد می‌کنند که نتیجه هر الگوریتم می‌تواند متفاوت باشد.

گراف کاملاً ترتیب پذیر

گراف G را کاملاً ترتیب پذیر[2] می‌گوییم اگر ترتیب π وجود داشته باشد به صورتی‌که با اعمال این ترتیب بر روی هر زیرگراف از گراف مفروض، الگوریتم آزمند و الگوریتم بهینه رنگ آمیزی، یکسان عمل کنند. به وسیلهٔ این ترتیب هیچ چهار راس aوbوcوd وجود ندارد که اگر در یک مسیر قرار داشته باشند راس a قبل از راس b و نیز راس c بعد از راس d قرار بگیرد. گراف‌های کاملاً ترتیب پذیر زیرمجموعه‌ای از گراف‌های کامل هستند اما تشخیص چنین گرافی یک مسئله ان‌پی-کامل[3] می‌باشد.

مجموعه‌های مختلفی از گراف‌های کاملاً ترتیب پذیر شناخته شده‌است برای مثال یک گراف مقایسه پذیر،[4] کاملاً ترتیب پذیر می‌باشد به این صورت که ترتیب رئوس آن به وسیلهٔ مرتب‌سازی توپولوژیک[5] تعیین می‌شود.

شبه کد

نمونه‌ای از شبه کد رنگ آمیزی آزمند:

پیوند به بیرون

پی‌نوشت
  1. Brooks' theorem
  2. Perfectly Orderable
  3. NP-Complete
  4. Comparability Graphs
  5. Topological Sort

منابع
  • ویکی‌پدیا انگلیسی،
  • ارائه یک مدل مبتنی بر رنگ آمیزی گراف برای تنظیم جداول زمانبندی دروس دانشگاهی، مریم معصومی، دکتر سید امیرحسن منجمی، دکتر ناصر نعمت بخش، دانشگاه اصفهان، دانشکده فنی، گروه کامپیوتر
  • داده ساختارها و مبانی الگوریتم‌ها، دکتر محمد قدسی
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.