روش تبدیل معکوس
روش تبدیل معکوس برای شبیهسازی متغیر تصادفی (نام علمی: Inverse transform sampling یا Inverse transformation method (همچنین شناختهشده تحت عناوین (inverse probability integral transform, Smirnov transform, universality of the uniform, یا golden rule[1])) یکی از روشهای عمومی برای شبیهسازی متغیرهای تصادفی روش تبدیل معکوس میباشد. گزاره: فرض کنید U یک متغیر تصادفی یکنواخت روی فاصله (۱و۰) باشد. برای هر تابع توزیع تجمعی پیوسته F اگر متغیر تصادفی Y را به وسیله Y=F^(-1) (U) تعریف کنیم، آنگاه متغیر تصادفی Y دارای تابع توزیع تجمعی F است. (F^(-1) (x) برابر آن مقدار y که F(y)=x است تعریف میشود.
- اثبات
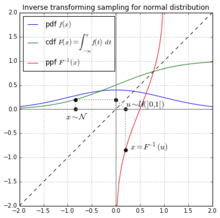
F_Y (a)=P{Y≤a} =P{F^(-1) (U)≤a} حال چون F(x) تابعی یکنواست، نتیجه میشود که F^(-1) (U)≤a اگر و فقط اگر U≤F(a). بدین ترتیب داریم: F_Y (a)=P{U≤F(a)} F(a) نتیجه میشود که میتوان متغیر تصادفی X را دارای تابع توزیع تجمعی پیوسته F است به وسیله تولید یک عدد تصادفی U و اختیار 〖X=F〗^(-1) (U) شبیهسازی کرد.
منابع
- راس، شلدرون. مبانی احتمال. ترجمهٔ احمد پارسیان و علی همدانی (ویراست ششم). انتشارات شیخ بهایی. ص. ۴۷۴.
- Aalto University, N. Hyvönen, Computational methods in inverse problems. Twelfth lecture https://users.aalto.fi/~nhyvonen/Lectures/cmip.pdf بایگانیشده در ۱۸ اکتبر ۲۰۱۹ توسط Wayback Machine