روش نمونهبرداری بازپسزننده
معرفی
در آنالیز عددی و محاسبات آماری، نمونهبرداری بازپسزننده (به انگلیسی: rejection sampling) روش پایهای برای تولید نمونه از یک توزیع احتمالی است که در آن به جای نمونهبرداری مستقیم از توزیع که دشوار است، از توزیع پیشنهادی که نمونهبرداری از آن ساده است استفاده میشود. اما توزیع پیشنهادی باید بهگونهای انتخاب شود که حداقل یک مقدار وجود داشته باشد بهطوریکه . با استفاده از توزیع نمونه را بدست میآوریم اما این نمونه با احتمال پذیرفته میشود. دلیل استفاده از بجای این است که با توجه به رابطه نمونهبرداری از سادهتر از است.[1]
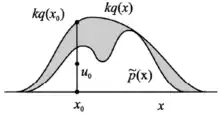
احتمال تولید شدن و پذیرفتن یک نمونه
در این روش احتمال تولید شدن یک نمونه دقبقا برابر با است.
همچنین احتمال پذیرش هر نمونه برابر است با:
به عبارت دیگر با افزایش مقدار احتمال پذیرش نمونهها کاهش مییابد.[1]
روش نمونهبرداری بازپسزننده تطبیقی
چالش اصلی در روش نمونهبرداری بازپسزننده تعیین توزیع پیشنهادی مناسب است. بطوریکه مقدار بگونهای انتخاب شود که احتمال پذیرفته نشدن نمونهها کاهش چشمگیری نداشته باشد. به عبارت دیگر در قسمت بالای منحنی قرار بگیرد و همچنین فاصله زیادی از آن نداشته باشد. در صورتیکه لگاریتم-مقعر باشد (به انگلیسی: log-concave) باشد با استفاده از روش نمونهبرداری بازپسزننده تطبیقی (به انگلیسی: Adaptive rejection sampling ) میتوان توزیع پیشنهادی مناسب را بدست آورد.[1]
فرآیند اجرا
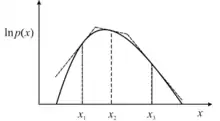
ابتدا با استفاده از توزیع یکنواخت تعدادی نمونه تولید میکنیم و برحسب احتمال گفته شده نمونهها را پذیرش و یا رد میکنیم. در صورت پذیرفته نشدن هر نمونه یک خط مماس بر توزیع اصلی در آن نقطه رسم میکنیم. درنتیجه از تقاطع حاصل از این خطوط یک توزیع حاصل میشود. با نمونه برداری از این توزیع و پذیرفتن نمونهها برحسب نسبت گفته شده، درصورت پذیرفته نشدن هر نمونه یک خط مماس جدید بر توزیع بدست آمده رسم میکنیم و فرآیند به همین ترتیب ادامه مییابد. با افزایش تعداد خطوط مماس، توزیع پیشنهادی بدست آمده پیچیدهتر میشود. اما باید توجه داشت که این خطوط در مقیاس لگاریتم رسم میشوند. در واقع با اجرای این فرآیند توزیعی بدست خواهد آمد که در مقیاس معمولی تکهای نمایی (به انگلیسی: piecewise exponential ) است، که نمونهبرداری از آن کار دشواری نیست.[1]
عملکرد نمونهبرداری بازپسزننده در ابعاد بالا
در روش نمونه برداری بازپسزننده با افزایش تعداد ابعاد توزیع موردنظر احتمال پذیرفتهشدن نمونهها بصورت نمایی کاهش مییابد. به عنوان مثال اگر دارای توزیع نرمال و دارای توزیع نرمال باشند بطوریکه و تفاوت بسیار ناچیزی داشته باشند و تعداد ابعاد هر کدام از این دو توزیع برابر باشند، در اینصورت میتوان متغیر تصادفی را بصورت نمایش داد.[1]
که در آن بردار میانگین با اندازه بعد است، و ماتریس کواریانس با ابعاد است.[2]
رابطه تابع چگالی احتمال برای توزیع نرمال چندمتغیره بصورت که در آن دترمینان ماتریس کواریانس است. ماتریس کواریانس یک ماتریس قطری است و میدانیم که دترمینان ماتریس قطری برابر است با حاصلضرب عناصر موجود در قطر اصلی، به عبارت دیگر برابر است با . از طرفی دیگر واریانس ابعاد مختلف یکسان است، بنابراین .
درنهایت با توجه به رابطه میتوان به این نتیجه رسید که .[1]
بنابراین حتی اگر فاصله بسیار کمی با داشته باشد، در ابعاد بالا عدد بسیار بزرگی خواهد بود و در نتیجه احتمال پذیرش نمونهها کاهش مییابد و به همین دلیل روش نمونهبرداری بازپسزننده در ابعاد بالا کاربردی نخواهد داشت و در این موارد از روشهایی از جمله گیبز و متروپلیس هستینگز استفاده میشود.
جستارهای وابسته
منابع
- Robert, C.P. and Casella, G. "Monte Carlo Statistical Methods" (second edition). New York: Springer-Verlag, 2004.
- J. von Neumann, "Various techniques used in connection with random digits. Monte Carlo methods", Nat. Bureau Standards, 12 (1951), pp. 36–38.