لم برنساید

در مسائل ترکیبیاتی به وفور مواردی یافت می‌شوند که علاقه‌مند به شمارش تعداد حالت‌های ممکن باشیم. این در حالتی است که عموماً بعضی حالت‌های در نظر گرفته شده با یکدیگر هم ارز هستند و با اعمال تبدیل‌های هم ریخت می‌توان آن‌ها را یکی در نظر گرفت. در این جا ساختار جبری گروه با ویژگی‌های مطلوب بسیار مورد توجه می‌باشد. از این رو داشتن اطلاعات اولیه راجع به این ساختار جبری توصیه می‌شود.

تاریخچه

این لم روشی برای شمارش افرازهایی است که در یک مجموعه به وسیله یک گروه از تبدیلات ایجاد می‌شود. این فرمول را ویلیام برنساید در سال ۱۸۹۷ در کتاب خود در مورد گروه‌های متناهی بیان کرد و آن را به فردیناند جورج فروبینیوس نسبت داد. اما پیش از آن نیز کوشی در سال ۱۸۴۵ مسائل مشابهی را از این روش حل کرده بود. اما به هر حال ویلیام برنساید برای اولین بار به شکل یک لم و با اثبات آن را مطرح کرد و کمک شایان توجهی در پیشروی نظریه گروه‌ها کرد.

شمارش و هم‌ارزی

مجموعه‌ای از اعضا مانند S را در نظر می‌گیریم. گروه G شامل مجموعه‌ای از توابع با دامنه S و برد S و عمل ترکیب دو تابع را در نظر می‌گیریم.

(G|G:S->S,ο)

در صورت اعمال به دسته‌های هم‌ارزی افراز می‌شود به نحوی که در هر یک از این دسته‌ها، هر عضو تحت عملی در G به سایر اعضای دسته قابل تبدیل است؛ و در عوض به اعضای سایر دسته‌ها قابل تبدیل نیست. رابطه R را به نحو زیر تعریف می‌کنیم:
برای o1≤i,j≤ |S|، C_i,C_j ∈ S داریم C_i R C_j اگر و تنها اگر C_j = G(C_i)
رابطه R با کیفیت بالا یک رابطه هم‌ارزی است. زیرا:

1. (ویژگی بازتابی): برای هر C_i ∈ S نتیجه می‌شود که C_i R C_i زیرا G شامل تابع همانی است. (C_i = I(C_i
2. (ویژگی تقارنی):اگر برای C_i,C_j ∈ S داشته باشیم C_i R C_j پس یک f ∈ G وجود دارد به نحوی که (C_j = f(C_i. از آنجا که G گروه است و در نتیجه شامل تابع معکوس f است. f⁻¹ ∈ G پس می‌توان گفت (C_i = f⁻¹(C_j و داریم: C_j R C_i.
3. (ویژگی ترایایی):فرض می‌کنیم C_i,C_j,C_k ∈ S و C_i R C_j و C_j R C_k در این صورت به ازای توابع f و g متعلق به G داریم (C_j = g(C_i)، C_k = g(C_j. با توجه به این که G گروه است و در نتیجه بسته است می‌توان گفت که h = fοg ∈ G در نتیجه (C_k = h(C_i پس C_i R C_k که این مؤید خصلت ترایایی می‌باشد.

شکل۲

پس R یک رابطه هم‌ارزی روی S است و آن را به رده‌های هم ارز افراز می‌کند. در نتیجه به راحتی قابل ملاحظه است که:

S=S₁ ∩ … ∩ S_k

C_j = f_k(C_i) ∈ S_m | f_k ∈ G,C_i ∈ S_m

برای درک بهتر موضوع توجه به مثال فوق ضروری است:
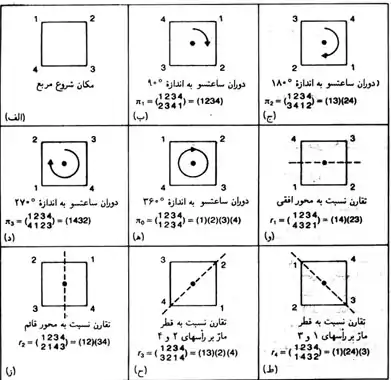
مربعی که هر یک از رئوس آن می‌تواند یکی از دو رنگ سیاه یا سفید را بپذیرد در نظر می‌گیریم. هر یک از حالت‌های ممکن را یکی از اعضای مجموعه S در نظر می‌گیریم. به این ترتیب S دارای ۱۶ = 4² عضو می‌باشد. حال مجموعه حرکت‌های سلب دورانی تقارنی را به عنوان مجموعه‌ای از توابع با دامنه و برد S در نظر می‌گیریم. این مجموعه با عنوان G در شکل نمایش داده شده است و شامل اعضای زیر است.

• π₀: دوران به اندازه ۳۶۰ درجه (¹₁²₂³₃⁴₄) = π₀ (در هر ردیف، رأس بالا به رأس پایین منتقل می‌شود. ۱ به ۱ و ۲ به ۲ و …)
• π₁: دوران به اندازه ۹۰ درجه (¹₂²₃³₄⁴₁) = π₁
• π₂: دوران به اندازه ۱۸۰ درجه (¹₃²₄³₁⁴₂) = π₂
• π₃: دوران به اندازه ۲۷۰ درجه (¹₄²₁³₂⁴₃) = π₃
• r₁: تقارن نسبت به محور افقی (¹₄²₃³₂⁴₁) = r₁
• r₂: تقارن نسبت به محور عمودی (¹₂²₁³₄⁴₃) = r₂
• r₃: تقارن نسبت به قطر اصلی (¹₃²₂³₁⁴₄) = r₃
• r₄: تقارن نسبت به قطر فرعی (¹₁²₄³₃⁴₂) = r₄

هر یک از این تبدیل‌ها را می‌توان به صورت حاصل ضرب دورهای مجزا نوشت که در هر یک از این دورها عناصر به صورت گردشی جابجا می‌شوند، برای مثال:
r₂ = (¹₂²₁³₄⁴₃) = 0(12). (۳۴)
π₂ = (¹₃²₄³₁⁴₂) = 0(1234)
در حالت کلی مشاهده می‌شود که این گروه G آبلی نیست.
در صورتی که تبدیل f بر مجموعه S اعمال شود، ^*f را تشکیل می‌دهد. در همین چارچوب به صورت حاصل ضرب دورهای مجزا می‌توان نوشت:
π₁^* = (C₁) (C₂C₃C₄C₅) (C₆C₇C₈C₉) (C₁₀C₁₁) (C₁₂C₁₃C₁₄C₁₅) (C₁₆)0

r₃^* = (C₁) (C₂)(C₃C₅)(C₄) (C₆C₇)(C₈C₉) (C₁₀)(C₁₁) (C₁₂C₁₄)(C₁₃C₁₅) (C₁₆)0
همان‌طور که مشاهده می‌شود، برای این دو نمونه و نیز سایر تبدیل‌ها، دوری وجود ندارد که بین دو دسته هم‌ارزی عضو مشترک داشته باشد.
در حالت کلی، S مجموعه پیکر بندیهاست و G تبدیل‌هایی که روی S عمل می‌کنند. رابطه R بر S به وسیله xRy تعریف شود، در صورتی که برای πهایی متلق به G باشد، π^* = y، آن گاه R یک رابطه هم‌ارزی است.

لم برنساید

تابع مولد دومتغیره زیر جهت شمارش تعداد پیکر بندی‌های نا هم ارز S برای حالت خاص بحث شده است.

f(r,w) = r⁴ + r³w + 2r²w² + rw³ + w⁴

که ضریب هر جمله تعداد پیکر بندی متمایزی که با i رنگ w و n-i رنگ r می‌توان درست کرد، می‌باشد. به این تابع فهرست الگویی می‌گویند.
در لم (قضیه) ای موسوم به برنساید رابطه‌ای برای شمارش تعداد این پیکر بندی‌های نا هم ارز ارائه شده است:

${\displaystyle {\frac {1}{|G|}}\sum _{\pi \in G}\psi (\pi ^{*})}$

که در آن (^*π)ψ تعدادی از پیکر بندی‌های S است که به وسیله ^*π تثبیت می‌شوند.

مثال کاربردی

به چند طریق می‌توان رئوس مربعی را رنگ آمیزی کرد به نحوی که امکان گردش در فضا وجود داشته باشد؟

برای حل از لم برنساید استفاده می‌کنیم:

• ${\displaystyle \psi (\pi _{0}^{*})=3^{4}}$ زیرا تبدیل همانی تمام پیکربندی‌های S را ثابت نگه می‌دارد.
• ${\displaystyle \psi (\pi _{1}^{*})=\psi (\pi _{3}^{*})=3}$ تنهای پیکربندی‌هایی را ثابت نگه می‌دارند که تمام رئوسشان رنگ یکسانی داشته باشند.
• ${\displaystyle \psi (\pi _{2}^{*})=3^{2}}$ برای دو رأس در انتخاب رنگ آزادی عمل داریم اما رنگ رئوس روبروی آنها باتوجه به رنگ این دو رأس تعیین می‌شود.
• ${\displaystyle \psi (r_{1}^{*})=r(\pi _{2}^{*})=3^{2}}$ این بار هم برای دو رأس در انتخاب رنگ آزادی عمل داریم اما رنگ رئوس مجاور آنها با توجه به رنگ این دو رأس تعیین می‌شود.
• ${\displaystyle \psi (r_{3}^{*})=r(\pi _{4}^{*})=3^{3}}$ در این تبدیل برای سه رأس آزادی انتخاب داریم. زیرا دو رأس اصلاً تغییر مکان نمی‌دهند و دو رأس دیگر که روبرو هستند همرنگ خواهند بود.

بنا براین:

${\displaystyle {\frac {3^{4}+3+3^{2}+3+3^{2}+3^{2}+3^{3}+3^{3}}{8}}=21}$

قضیه برنساید

بعضاً از لم برنساید با عنوان قضیه برنساید یاد می‌شود.

در صورتی که قضیه‌ای دیگر در نظریه گروه‌ها وجود دارد که موسوم به قضیه برنساید است.

این قضیه بیان می‌کند که هر گروه که مرتبه آن به شکل ${\displaystyle p^{a}q^{b}}$(که p,q اعداد اول و a,b اعداد طبیعی هستند) قابل تجزیه باشد یک گروه حل پذیر است.

نخستین نتیجه‌ای که از این قضیه گرفته می‌شود این است که اگر یک گروه غیر آبلی ساده متناهی داشته باشیم، از مرتبه‌ای تجذیه پذیر به سه عامل اول خواهد بود.

منابع

• رالف گریمالدی (۱۳۸۵)، ریاضیات گسسته و ترکیبیاتی از دیدگاه کاربردی حلد دوم، ترجمهٔ محمد علی عمیدی، تهران: مرکز نشر دانشگاهی، شابک ۹۶۴-۰۱-۰۸۹۰-۱
• مشارکت‌کنندگان ویکی‌پدیا. «Burnside`s lemma». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در آوریل ۲۰۱۰.
• مشارکت‌کنندگان ویکی‌پدیا. «Burnside theorem». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در آوریل ۲۰۱۰.