نقطه کانونی (نظریه بازی‌ها)

نقطهٔ کانونی در نظریهٔ بازی یک راه‌حل است که وقتی افراد امکان برقراری ارتباط با یکدیگر را ندارند، از آن استفاده می‌کنند. این نقطه به این دلیل راه‌حل است که به نوعی متمایز از دیگر انتخاب‌های موجود و کانون توجه است به همین دلیل به آن نقطهٔ کانونی یا متمایز می‌گویند. توماس شیلینگ این مفهوم را برای اولین بار در کتاب معروف خود به نام استراتژی برخورد،[1] معرفی کرد؛ به همین دلیل به آن نقطهٔ شیلینگ نیز می‌گویند.

معرفی[2]

فرض کنید یک مربع ۲*۲ به دو نفر که حق برقراری ارتباط با یکدیگر را ندارند نشان داده می‌شود و از هرنفر خواسته می‌شود یک خانه را انتخاب کند. خانه‌ها هیچ تفاوتی با یکدیگر ندارند. اگر هر دو نفر یک خانه را انتخاب کنند ۱۰ دلار پاداش می‌گیرند و در غیر اینصورت هیچ پاداشی دریافت نمی‌کنند. از آنجایی که هیچ تفاوتی بین خانه‌ها وجود ندارد و افراد با هم ارتباطی ندارند انتخاب خانه‌ای که منجر به برد شود کار آسانی نیست.

حل بازی‌هایی به این شکل نیاز به یک روحیهٔ تیمی داردو هر دو طرف بازی می‌خواهند یک استراتژی را اتخاذ کنند تا برنده شوند. به بازی‌هایی از این دست بازی هماهنگی می‌گویند. در بازی بالا هیچ خانه‌ای بهتر از دیگری نیست و دستاورد طرفین بازی تنها به اینکه انتخاب یکسانی داشته باشند بستگی دارد، مثلاً اگر دو نفر با یکدیگر دوست باشند؛ دانش عمومیای(commen knowledge) که نسبت به یکدیگر دارند می‌تواند در برنده شدن به افراد کمک کند مثلاً یکی از افراد خانهٔ شماره ۴ را انتخاب می‌کند چون عدد مورد علاقهٔ دوستش است. اما اگر دو نفر کاملاً با یکدیگر غریبه باشندهیچ راهی جز اینکه به صورت کاملاً تصادفی یک خانه را انتخاب کنند و با احتمال ۰٫۲۵ برنده شوند؛ ندارند.

حال فرض کنید بازی را به این شکل تغییر دهیم که خانهٔ شماره ۲ را علامت‌دار کنیم.

یک بازی هماهنگی ساده

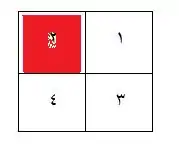
در این حالت خانهٔ شماره ۲ بیش از سایر خانه‌ها توجه را به خود جلب می‌کند و هر فرد ممکن است به امید اینکه این خانه توجه هم‌بازی‌اش را نیز جلب کند، خانهٔ ۲ را انتخاب کند. علامت دار کردن خانهٔ ۲ باعث می‌شود که افراد به صورت طبیعی این خانه را انتخاب کنند. هیچ نکته یا دستاورد خاصی در انتخاب خانهٔ ۲ نیست. تعادل‌های دیگر بازی انتخاب همانند هر کدام از خانه‌های دیگر است. آنچه که خانهٔ ۲ را خاص می‌کند علامت دار کردن آن و جلب توجه به سمت آن است. به تعادل‌هایی به این شکل نقطهٔ کانونی می‌گویند. به این نکته باید توجه‌کنیم که نقاط کانونی به فاکتورهایی مثل باورهای اجتماعی بستگی دارند. مثلاً ممکن است در یک فرهنگ عدد ۲ عدد دلخواهی نباشد و به همین دلیل هیچ‌کس خانهٔ ۲ را انتخاب نکند که این حالت هم مفید است از آنجا که باعث می‌شود احتمال برد از ۰٫۲۵ به ۰٫۳۳ افزایش پیدا کند.

نقطهٔ کانونی ایستا[3]

نقطه‌ای کانونی که بر اساس برداشت ثابت افراد از بازی باشد مانند بازی مطرح شده در بالا.

نقطهٔ کانونی پویا[3]

نقطه‌ای کانونی ای که بر اساس برداشت افراد در حین بازی باشد مثلاً اگر زن و شوهری یکدیگر را در خیابان گم کنند و به صورت اتفاقی در مغازهٔ اسباب‌بازی فروشی یکدیگر را ملاقات کنند؛ بار بعد که یکدیگر را گم کنند مغازهٔ اسباب‌بازی فروشی یک نقطهٔ کانونی است در حالی که بار اول که یکدیگر را گم کردند، آن انتخاب نقطهٔ کانونی بازی نبود.

نقطهٔ کانونی در بازی هماهنگی خالص[3][4]
  • بازی هماهنگی خالص:

بازی هماهنگی ای است که دستاورد طرفین بازی از هر نتیجهٔ بازی یکسان است. بازی‌های همانگی خالص معمولاً بیش از یک تعادل نش دارند اما برخلاف اینکه دستاورد بازیکنان از هر نتیجهٔ بازی یکسان است الزامی ندارد که ترجیحاتشان میان تعادل‌های موجود متفاوت نباشد (مثل انتخاب خانهٔ ۲ در بازی قبل) در واقع بازیکنان، بعضی از تعادل‌های نش بازی را به بعضی دیگر ترجیح می‌دهند و تعادل بازی پرتو-رتبه‌بندی است.

  • بازی‌های جورسازی(matching games):

بازی‌های هماهنگی ای هستند که درآنها بازیکن‌ها با استراتژی‌های یکسان و ترجیحات بر نتایج بازی با یکدیگر بازی می‌کنند. دستاوردها(pay off) تنها در حالتی مثبت هستند که همهٔ بازیکنان یک انتخاب داشته باشند در غیر اینصورت دستاوردها صفر هستند. بازی‌های جورسازی مشکل هماهنگی را به ساده‌ترین و واضح‌ترین شکل ممکن نشان می‌دهد.

در یک بازی هماهنگی خالص یک تعادل نش به دو دلیل می‌تواند متمایز از دیگر تعادل‌ها باشد ۱- به دلیل ویژگی‌های ریاضی بازی مانند دستاورد بالاتر ۲- به دلیل روشی که بازیکنان بازی را برای خود شکل می‌دهند. اگر مورد ۲ دلیل تمایز باشد (نقطهٔ کانونی) یعنی بازی ویژگی‌ای دارد که در مدل ریاضی آن تبیین نشده‌است.

آیا انتخاب‌های کانونی با عقلانیت تطابق دارند؟

نظریهٔ بازی استاندارد بر اساس فرض وجود دانش همگانی (common knowledge rationality) بنا شده‌است. نتیجهٔ مستقیم فرض وجود دانش عمومی، شفافیت استدلال است. از فرض دانش عمومی و بیشینه کردن مطلوبیت نتیجه می‌شود که بازی هماهنگی خالص یا هر بازی دیگر اگر راه حلی یکتا داشته باشد آن راه حل حتماً باید تعادل نش باشد. در بازی‌های هماهنگی خالص یا هر بازی ای به جز بازی‌های اکیداً رقابتی (دو نفره -جمع صفر) روش‌های معمول، کمکی به یافتن راه حل یکتای بازی نمی‌کند زیرا این بازی‌ها معمولاً چند تعادل نش دارند. شیلینگ نشان داد که تحلیل‌های شهودی بازی‌های هماهنگی خالص منجر به راه حل نقطهٔ کانونی می‌شود. شواهد و آزمایش‌های تجربی نیز این یافته را تأیید می‌کنند. مارگارت گیلبرت نشان داد که هماهنگی موفق نمی‌تواند نتیجهٔ عقلانیت باشد.

نکته‌ای که وجود دارد این است که عقلایی بودن در اینجا به نوعی خود را شکست می‌دهد(self-defeating). فرض کنید در یک بازی جورسازی بازیکن ۱ می‌داند که دیگری مستقل از عقلانیت، تعادل نش متمایز را انتخاب‌می‌کند که در نتیجه یعنی بازیکن ۲ غیر عقلایی رفتارمی‌کند و بازیکن ۱ با یک توجیه عقلایی و به دلیل بیشینه کردن مطلوبیت، همان تعادل نش متمایز را انتخاب‌می‌کند و هماهنگی به راحتی انجام‌می‌شود. این نتیجهٔ مهم که نقطهٔ کانونی در بازی هماهنگی خالص در چارچوب فروض عقلانیت استاندارد قابل توجیه نیست، در ادبیات نظریهٔ بازی پذیرفته‌شده‌است.

کاهش حالت هماهنگی خالص به حالت دستاورد غالب
  • تعادل دستاورد غالب: تعادلی است که در آن دستاورد یکی از تعادل‌های نش برای تمامی بازیکنان از تمامی تعادل‌های نش دیگر بیشتر است.
  • اصل دستاورد غالب: اگر در بازی یک تعادل دستاورد غالب وجودداشته‌باشد آنگاه بازیکنان عقلایی استراتژی متناظر با آن دستاورد را انتخاب‌می‌کنند.

بازی ای که در ادامه می‌آید هر بازی جورسازی را که یک نقطهٔ کانونی دارد؛ مدل می‌کند:

به دو بازیکن مهره نشان داده می‌شود. مهره سفید رنگ و ۱ مهره آبی رنگ است. هر بازیکن یکی از مهره‌ها را بدون اطلاع از انتخاب باریکن دیگر انتخاب می‌کند. اگر هر دو بازیکن یک مهره را انتخاب کنند دستاوردی به اندازهٔ ۱ واحد مطلوبیت دریافت می‌کنند در غیر اینصورت هیچ دستاوردی نخواهندداشت. همچنین فرض می‌شود اگر بازیکن‌ها مهرهٔ سفید را انتخاب کنند راهی برای تشخیص اینکه مهره‌های انتخاب شده مانند هم هستند یا نه وجود دارد ولی بازیکن‌ها نمی‌توانند مهره‌های سفید را از یکدیگر تشخیص دهند. در ضمن m هم به اندازهٔ کافی بزرگ است.

به‌طور شهودی بازیکن‌ها باید مهرهٔ آبی را انتخاب کنند در حالی که در غالب تئوری دلیل این انتخاب، واضح نیست.

مدل کردن ماتریس دستاوردهای این بازی به شکل یک ماتریس تبیین صحیحی نیست چرا که بازیکن‌ها ظرفیت انتخاب از میان استراتژی را ندارند و مهره‌های سفید برای بازیکن‌ها قابل تمایز نیست پس در واقع هر بازیکن سه استراتژی دارد: ۱- انتخاب مهرهٔ آبی ۲- انتخاب مهرهٔ سفید ۳- انتخاب یک مهره به صورت تصادفی

ماتریس دستاوردهای بازی به شکل زیر در می‌آید:

ماتریس دستاوردها برای بازی مهرهٔ آبی

همان‌طور که ماتریس نشان می‌دهد بازی ۳ تعادل نش دارد که از میان آن‌ها حالت تعادل نش با دستاورد غالب است. اگر توجیهی عقلایی برای انتخاب تعادل نش با دستاور غالب در این بازی وجود داشته‌باشد آنگاه توجیهی عقلایی برای توجه به تعادل‌های متمایز (نقاط کانونی) نیز وجود دارد. حال بازی قبل را به حالتی عمومی‌تر بسط می‌دهیم.

بازی قبل را در حالتی که تمامی مهره‌ها سفید رنگ هستند در نظرمی‌گیریم. دو بازیکن مانند قبل بازی می‌کنند و سعی دارند که یک مهره را انتخاب کنند اگر مهره‌های سفید غیرقابل تمایز باشند، نقطهٔ کانونی ای وجود ندارد و هر بازیکن یک مهره را تصادفی انتخاب می‌کند و دستاوردی به اندازه به‌دست‌می‌آورد. حال این فرض را در نظر می‌گیریم که یکی از مهره‌ها شکستگی یا علامتی دارد که برای هر بازیکن ممکن است قابل تشخیص باشد یا نباشد. اگر یکی از بازیکنان مهرهٔ متمایز را شناسایی کند، احتمالی بزرگتر از صفر به این پیشامد که بازیکن دیگر نیز این مهره را شناسایی کند، نسبت می‌دهد. اگر هردو بازیکن مطمئن باشند که طرف مقابلشان مهره را شناسایی می‌کند، احتمال نسبت داده شده ۱ است و طرفین به نقطهٔ تعادل بازی هماهنگی می‌رسند. در این شرایط دو حالت متفاوت بازی مهره‌ها، یکریخت هستند و توجیه عقلایی نقطهٔ کانونی به عنوان نتیجهٔ هر توجیه عقلایی اصل دستاورد غالب به دست می‌آید.

در نظریهٔ چارچوب متغیر، آگاهی یک فرد از ویژگی خاص، یک متغیر تصادفی است و هر بازیکن به این پیشامد که بازیکن دیگر نیز این ویژگی را مشاهده کند احتمالی نسبت می‌دهد. در حالتی از بازی که مهره‌ها سفید هستند اگر هر دو نفر توانایی تشخیص مهرهٔ متمایز را داشته باشند و احتمال p را به تشخیص این ویژگی از طرف دیگر تخصیص دهند؛ آنگاه نقطهٔ کانونی وجود دارد و مطلوبیت افراد با انتخاب آن بیشینه می‌شود. نقطهٔ کانونی همچنان یک نقطهٔ تعادل با دستاورد غالب است که در نتیجهٔ انتخاب آن با در نظر گرفتن هر توجیهی برای اصل دستاورد غالب یک توجیه عقلایی دارد.

اگر بیش از یک انتخاب متمایز برای بازیکنان وجود داشته باشد و همهٔ بازیکنان متوجه تمایزهای موجود بشوند و به اینکه طرفشان نیز این ویژگی را تشخیص می‌دهد نیز احتمالی نسبت دهند؛ آنگاه اگر هر دو بازیکن استراتژی‌ای را انتخاب کنند که یکی از نقاط متمایز را تصادفی انتخاب کنند، نتیجهٔ بازی یک تعادل نش با دستاورد غالب خواهد بود.

پروسهٔ استکلبرگ

ارائهٔ یک توضیح قانع‌کننده برای اصل دستاورد غالب، به طرز غیرمنتظره‌ای دشوار است. بسیاری از توضیحات ارائه شده از اصول نظریهٔ بازی استاندارد بسیار دور است. کالمن و باچاراه در قالب پروسهٔ استکلبرگ، توضیحی ارائه می‌کنند که نسبت به توضیحات دیگر از فروض نظریهٔ بازی استاندارد، کمتر دور است. پروسهٔ مورد نظر به این شکل است که هر بازیکن در مقابل هر استراتژی فرد دیگر، بهترین بازی خود را که ماکزیمم‌کنندهٔ مطلوبیتش است؛ انجام می‌دهد. اگر فرض شفافیت استدلال را مبنی بر اینکه هر نتیجه‌ای که یکی از بازیکنان در مورد استراتژی انتخابی اش می‌گیرد توسط بازیکن دیگر قابل پیش‌بینی است؛ بپذیریم آنگاه هر بازیکن بر اساس این فرض که فرد دیگر هم به صورت غیر متغیری بهترین جواب را انتخاب می‌کند؛ استراتژی‌ای را انتخاب می‌کند که مطلوبیتش را ماکزیمم می‌کند. یعنی از بین تمامی نقاط تعادل بازی، نقطهٔ تعادل با دستاورد غالب انتخاب می‌شود.

نقاط کانونی اجتماعی[5]

تحقیقات نشان داده‌اند که وقتی افراد با تصمیمات هماهنگی مواجه می‌شوند بیشتر به دنبال نقاط کانونی هستند برای تصمیم‌گیری تا انتخاب از میان استراتژی‌هایی که هیچ وجه تمایزی برایشان ندارند. در واقع افراد از اطلاعاتی مستقل از دستاوردهای بازی برای رسیدن به یک عمل مشترک استفاده می‌کنند. در قسمتی از این تحقیقات به مطالعهٔ سیاست‌های هویتی از طریق بررسی نقش هویت در حل مشکلات هماهنگی پرداخته شده‌است. در زمینه‌های بسیاری اثرات هماهنگی خالص همانند مکانیزم‌های معمولی هستند که هویت را به عمل مشترک (مثل ترجیحات یا نرم‌های اجتماعی) مرتبط می‌کنند. در قسمتی از این پژوهش‌ها به آزمون این فرضیه پرداخته‌اند که افراد، جنسیت و نژاد را به عنوان ابزار هماهنگ‌کننده استفاده می‌کنند.

در این پژوهش‌ها نشان داده شده‌است که افراد از طریق هویت نژادی با یکدیگر هماهنگ می‌شوند. همچنین شواهد ضعیف تری یافت شده‌است مبنی بر هماهنگی از طریق جنسیت با وجود آن که شناسایی جنسیت راحت‌تر از شناسایی نژاد است. همچنین تحقیقات نشان داده‌اند در هماهنگی از طریق جنسیت، زنان همجهت با جنسیت و مردان در خلاف جهت آن عمل می‌کنند (مثلاً در یک بازی دیکتاتور زنان به زنان و مردان به زنان، بیشتر جایزه می‌دهند). اما در این مورد بر خلاف مورد هماهنگی از طریق ویژگی‌های نژادی، این فرضیه که اشکال مختلف هماهنگی موفق که بر اساس جنسیت است، برآمده از نُرم‌های اجتماعی ای است که نوع رفتار بین زنان و مردان را شکل داده است؛ رد نمی‌شود.

بیشتر تئوری‌های استاندارد در مورد نقش هویت اجتماعی در تصمیم‌گیری‌های استراتژیک بر تفاوت باورها و نظرات انواع مختلف افراد، وابستگی افراد به اعضای داخل گروه و بیرون گروه و نُرم‌های اجتماعی ای برآمده از هویت گروه که رفتار اعضای آن را شکل می‌دهد؛ تأکید دارند. در مثال‌های زیادی این ویژگی‌ها مهم هستند (مکانیزم‌های متفاوتی که می‌تواند کاربرد گروه‌های هویتی در سیاست را توضیح دهد، بسته به زمینهٔ سیاسی ممکن است متفاوت باشد) اما پژوهش مذکور نشان می‌دهد که هیچ‌کدام از این ویژگی‌ها برای توضیح ساختار سیاست از طریق هویت، الزامی نیست. در واقع شکل توزیعی محیط سیاسی، مهم تر از انگیزه‌های افراد برای رفتارهای خوب یا بد با یکدیگر است. وقتی ساختارهای سیاسی افراد را به شکل‌دهی ائتلاف‌ها سوق می‌دهند، توانایی افراد برای دسته‌بندی و دسته‌بندی شدن مهم تر از معناداری دسته‌ای است که در آن هستند.

منابع
  1. Schelling، Thomas. The Strategy of Conflict.
  2. https://mindyourdecisions.com/blog/2008/04/01/focal-points-or-schelling-points-how-we-naturally-organize-in-games-of-coordination. پارامتر |عنوان= یا |title= ناموجود یا خالی (کمک)
  3. Casajus، Andre Casajus. Focal Points in Framed Games.
  4. Andrew M. Colman. https://www2.le.ac.uk/departments/npb/people/amc/articles-pdfs/salifocu.pdf. پارامتر |عنوان= یا |title= ناموجود یا خالی (کمک); پیوند خارجی در |وبگاه= وجود دارد (کمک); پارامتر |پیوند= ناموجود یا خالی (کمک)
  5. James Habyarimana,Macartan Humphreys,Daniel Posner,Jeremy Weinstein. http://www.columbia.edu/~mh2245/papers1/coordination.pdf. پارامتر |عنوان= یا |title= ناموجود یا خالی (کمک); پیوند خارجی در |وبگاه= وجود دارد (کمک); پارامتر |پیوند= ناموجود یا خالی (کمک)

مطالعهٔ بیشتر

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.