هرم کمینه-بیشینه
در علوم رایانه، هرم کمینه بیشینه یک درخت دودویی کامل است که فواید هرم کمینه و هرم بیشینه را با هم ترکیب کرده است. این ساختمان داده به ما این امکان را می دهد تا عنصر بیشینه و کمینه را
در زمان ثابت ((1)O) بازگرداند یا در زمان لگاریتمی((logn)O) آن ها را حذف کنیم.[1] این قابلیت هرم کمینه بیشینه را به یک ساختمان داده مفید برای پیاده سازی یک صف اولویت دو طرفه تبدیل می کند.
همانند هرم کمینه و هرم بیشینه دودویی، هرم کمینه بیشینه عملیات های درج و حذف را در زمان لگاریتمی انجام می دهد و در زمان خطی ساخته می شود.[2] هرم کمینه بیشینه معمولا در آرایه ساخته می شود [3] به همین دلیل به عنوان یک ساختمان داده ضمنی از آن یاد می شود.
مشخصه ی یک هرم کمینه بیشینه :
هر گره در سطح زوج در درخت دودویی متناظر با هرم از تمام گره های موجود در زیردرخت خود کوچکتر است درحالی که هر گره در سطح فرد در درخت متناظر با هرم از تمام گره های زیردرخت خود بزرگتر است.[3]
این ساختار همچنین می تواند به گونه ای تعمیم داده شود تا عملیات هایی مثل پیدا کردن میانه(find-median) و (delete-median) حذف کردن میانه[1] ، پیدا کردن kامین کوچکترین مقدار در ساختار((find(k) و عملیات حذف کردن kامین کوچکترین مقدار در ساختار((delete(k) را به ازای یک مقدار مشخص یا مجموعه ای از مقادیر k انجام دهد. این داده ساختار دو عملیات انتهایی را میتواند به ترتیب در زمان های خطی و لگاریتمی انجام دهد. مفهوم ترتیب کمینه بیشینه میتواند به ساختارهای دیگری که بر پایه ترتیب بیشینه یا کمینه هستند گسترش پیدا کند مانند درخت چپ گرا (leftist trees) که منجر به ایجاد یک دسته جدید و قدرتمند از داده ساختارها می شود.[3] هرم کمینه بیشینه همچنین برای پیاده سازی مرتب سازی سریع خارجی نیز مفید است. [5]
توضیحات
معرفی
- هرم کمینه بیشنه یک درخت دودویی کامل است که شامل سطوح کمینه (زوج) و بیشینه (فرد) است. سطوح زوج 0،2،4،... و سطوح فرد 1،3،5،... . همچنین فرض می کنیم عنصر ریشه در سطح اول (0) قرار دارد.
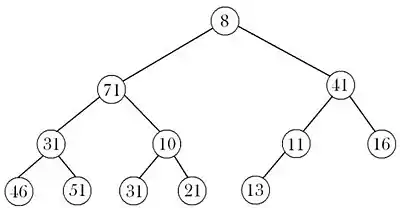
- عنصر ریشه کوچکترین عنصر موجود در هرم کمینه بیشینه است.
- یکی از دو گره موجود در سطح دوم که سطح بیشینه (فرد) است، عنصر بیشینه در هرم کمینه بیشینه است.
- فرض کنید x یک گره دلخواه در هرم کمینه بیشینه است. در این صورت :
- اگر x در سطح کمینه (یا زوج) قرار داشته باشد در اینصورت کلید آن از کلید همه عناصر موجود در زیردرختی که ریشه آن x است کمتر است.
- اگرx در سطح بیشینه (یا فرد) قرار داشته باشد در اینصورت کلید آن از کلید همه عناصر موجود در زیردرختی که ریشه آن x است بیشتر است.
هرم بیشینه کمینه به صورت معکوس تعریف می شود. در این هرم مقدار بیشینه در ریشه ذخیره می شود و مقدار کمینه در یکی از دو گره فرزند ریشه ذخیره می شود.
عملیات
در عملیات های زیر فرض می کنیم که هرم کمینه بیشینه در یک آرایه قرار دارد. خانه ی iام آرایه به گرهی اشاره میکند که در سطح قرار دارد.
ساخت هرم
ساختن یک هرم کمینه بیشینه با انجام تغییراتی در الگوریتم ساخت هرم Floyd در زمان خطی انجام می شود که روشی از پایین به بالا است.[3] الگوریتم ساخت هرم Floyd[4] به صورت زیر است :
function FLOYD-BUILD-HEAP(h):
for each index i from down to 1 do:
push-down(h, i)
return h
در این تابع، h آرایه اولیه است که لزوما عناصر آن خواص هرم کمینه بیشینه را ندارد. عملیات push-down (که گاهی heapify گفته می شود) برای یک هرم کمینه بیشینه در قسمت بعد توضیح داده شده است.
پایین بردن مقدار در هرم (push-down)
الگوریتم push-down (یا trickle-down همانطور که در [3] گفته شده) به صورت زیر است :
function PUSH-DOWN(h, i):
if i is on a min level then:
PUSH-DOWN-MIN(h, i)
else:
PUSH-DOWN-MAX(h, i)
endif
پایین بردن مقدار کمینه (push down min)
function PUSH-DOWN-MIN(h, i):
if i has children then:
m := index of the smallest child or grandchild of i
if m is a grandchild of i then:
if h[m] < h[i] then:
swap h[m] and h[i]
if h[m] > h[parent(m)] then:
swap h[m] and h[parent(m)]
endif
PUSH-DOWN-MIN(h, m)
endif
else if h[m] < h[i] then:
swap h[m] and h[i]
endif
endif
پایین بردن مقدار بیشینه (push down max)
الگوریتم مربوط به push-down-max دقیقا مشابه الگوریتم push-down-min است با این تفاوت که جهت عملگرهای مقایسه را برعکس می کنیم.
function PUSH-DOWN-MAX(h, i):
if i has children then:
m := index of the largest child or grandchild of i
if m is a grandchild of i then:
if h[m] > h[i] then:
swap h[m] and h[i]
if h[m] < h[parent(m)] then:
swap h[m] and h[parent(m)]
endif
PUSH-DOWN-MAX(h, m)
endif
else if h[m] > h[i] then:
swap h[m] and h[i]
endif
endif
فرم پیمایشی
همچنین می توانیم به جای استفاده از توابع بازگشتی که در بالا اشاره شد از شکل پیمایشی آن استفاده کنیم که این کار را با حافظه ی ثابت انجام میدهد.
function PUSH-DOWN-MIN-ITER(h, m):
while m has children then:
i := m
m := index of the smallest child or grandchild of i
if m is a grandchild of i then:
if h[m] < h[i] then:
swap h[m] and h[i]
if h[m] > h[parent(m)] then:
swap h[m] and h[parent(m)]
endif
endif
else if h[m] < h[i] then:
swap h[m] and h[i]
endif
endwhile
درج یک عنصر
برای درج یک عنصر در هرم کمینه-بیشینه باید اعمال زیر را انجام دهیم:
- کلید عنصر را در انتهای آرایه ای که هرم کمینه بیشینه در آن نگهداری می شود قرار می دهیم. این کار به احتمال زیاد ویژگی هرم کمینه بیشینه را در آرایه از بین می برد، به همین دلیل آرایه را باید دوباره سازگار کنیم.
- کلید این عنصر را با پدرش مقایسه میکنیم :
- اگر کوچکتر (بزرگتر) بود مطمئناً از کلید تمام گرههای سطح بیشینه (کمینه) که از مکان فعلی کلید تا ریشه هرم قرار دارد کوچکتر است. حال کافی است تا با گرههای سطح کمینه (بیشینه) مقایسه شوند.
- مسیر از عنصر جدید تا ریشه (با در نظر گرفتن تنها سطوح کمینه (بیشینه)) باید به صورت نزولی (صعودی) به همان صورتی که قبل از درج قرار داشت، باشد. پس باید با استفاده از درج دودویی عنصر جدید را در رشته قرار دهیم. روش ساده تر این است که عنصر جدید را تا زمانی که از پدرش کوچکتر (بزرگتر) است با پدرش جابه جا کنیم.
بالابردن مقدار (Push up)
الگوریتم push-up (یا Bubble-up همانطور که در [5] گفته شده است) به صورت زیر است.
function PUSH-UP(h, i):
if i is not the root then:
if i is on a min level then:
if h[i] > h[parent(i)] then:
swap h[i] and h[parent(i)]
PUSH-UP-MAX(h, parent(i))
else:
PUSH-UP-MIN(h, i)
endif
else:
if h[i] < h[parent(i)] then:
swap h[i] and h[parent(i)]
PUSH-UP-MIN(h, parent(i))
else:
PUSH-UP-MAX(h, i)
endif
endif
endif
بالابردن مقدار کمینه (push up min)
function PUSH-UP-MIN(h, i):
if i has a grandparent and h[i] < h[grandparent(i)] then:
swap h[i] and h[grandparent(i)]
PUSH-UP-MIN(h, grandparent(i))
endif
بالابردن مقدار بیشینه (push up max)
الگوریتم push-up-max همانند الگورریتم push-up-min است با این تفاوت که جهت عملگر های مقایسه را برعکس می کنیم.
function PUSH-UP-MAX(h, i):
if i has a grandparent and h[i] > h[grandparent(i)] then:
swap h[i] and h[grandparent(i)]
PUSH-UP-MAX(h, grandparent(i))
endif
فرم پیمایشی
همچنین می توانیم به جای استفاده از توابع بازگشتی که در بالا اشاره شد از شکل پیمایشی آن استفاده کنیم که این کار را با حافظه ی ثابت انجام میدهد.
function PUSH-UP-MIN-ITER(h, i):
while i has a grandparent and h[i] < h[grandparent(i)] then:
swap h[i] and h[grandparent(i)]
i := grandparent(i)
endwhile
مثالی از درج یک عنصر در هرم کمینه-بیشینه.
ما هرم کمینه-بیشینه زیر را داریم و میخواهیم عنصری با مقدار ۶ را در آن درج کنیم.
در ابتدا عنصر ۶ را در مکان مشخص شده با j قرار میدهیم. عنصر ۶ از پدرش کوچکتر است لذا از تمام عناصر سطوح بیشینه کمتر است. بابراین عنصر ۶ در مکان ریشه درخت قرار میگیرد و عنصر قبلی ریشه یک گام به پایین نقل مکان میکند.
اگر بخواهیم یک عنصر جدید با مقدار ۸۱ را در هرم مفروض قرار دهیم، مانند قبل جلو میرویم. در ابتدا عنصر ۸۱ را در مکان مشخص شده با j قرار میدهیم. از آنجا که عنصر ۸۱ از پدرش و تمام عناصر سطوح کمینه بیشتر است کافی است گرههای سطح بیشینه بررسی شوند.
حذف کوچکترین کلید
برای حذف کوچکترین کلید در هرم کمینه-بیشینه باید اعمال زیر را انجام دهیم.
گره درخت کوچکترین عنصر است.
- گره ریشه را حذف میکنیم و فرض میکنیم x گرهای باشد که در انتهای هرم قرار دارد.
- حال x را در هرم کمینه-بیشینه دوباره درج میکنیم.
برای دوباره درج کردن دو وضعیت به وجود میآید.
اگر ریشه هیچ فرزندی نداشته باشد، پس x میتواند در ریشه قرار گیرد.
فرض کنید ریشه حداقل یک فرزند داشته باشد. مقدار کمینه را پیدا میکنیم و این عنصر را m مینامیم. m یکی از فرزندان یا نوادگان ریشه است. حال شرایط زیر باید در نظر گرفته شود:
- اگر x.key <= h[m].key آنگاه x باید در مکان ریشه قرار گیرد.
- اگر x.key> h[m].key و m فرزند ریشه باشد چون m در سطح بیشینه است، هیچ فرزندی ندارد بنابراین عنصر [h[m باید در مکان ریشه و عنصر x در گره m قرار گیرد.
- اگر x.key> h[m].key و m از نوادگان فرزند ریشه باشد آنگاه باید عنصر [h[m در مکان ریشه قرار گیرد. حال فرض کنیم p پدر m باشد، اگر x.key> h[p].key آنگاه جایگاه [h[p و x باید عوض شود.
کد زیر حذف عنصر با کوچکترین کلید را پیادهسازی میکند.
element del_min(element heap[], int *s) { // *s: capacity of the heap
int i, last, m, parent;
element temp, x;
if ((*s) == 0) {
heap[0].key = INT_MAX;
return(heap[0]);
}
heap[0] = heap[1];
x = heap[(*s)--];
/* find place to insert x */
for (i = 1, last = (*s) / 2; i <= last; ) {
m = min_child_grandchild(i, *s);
if (x.key <= heap[m].key) // case 1
break;
heap[i] = heap[m]; // case 2 or 3
if (m <= (2 * i) + 1) { // case 2
i = m;
break;
}
/* case 3 */
parent = m / 2;
if (x.key > heap[parent].key)
SWAP(heap[parent], x, temp);
i = m;
}
heap[i] = x;
return heap[0];
}
منابع
- Atkinson, M. D.; Sack, J.-R.; Santoro, B.; Strothotte, T. (1986-10-01). "Min-max heaps and generalized priority queues". Communications of the ACM. 29 (10): 996–1000. doi:10.1145/6617.6621.
- Atkinson, M. D.; Sack, J.-R.; Santoro, B.; Strothotte, T. (1986-10-01). "Min-max heaps and generalized priority queues". Communications of the ACM. 29 (10): 996–1000. doi:10.1145/6617.6621.
- Atkinson, M. D.; Sack, J.-R.; Santoro, B.; Strothotte, T. (1986-10-01). "Min-max heaps and generalized priority queues". Communications of the ACM. 29 (10): 996–1000. doi:10.1145/6617.6621.
- یادکرد خالی (کمک)
- Atkinson, M. D.; Sack, J.-R.; Santoro, B.; Strothotte, T. (1986-10-01). "Min-max heaps and generalized priority queues". Communications of the ACM. 29 (10): 996–1000. doi:10.1145/6617.6621.
- M. D. Atkinson, J.R. Sack, N. Santoro, and T. Strothotte, Communications of the ACM, October, 1986, Min-Max Heaps and Generalized Priority Queues.
- Jiwan Pokharel, Department of Computer Science
Loyola University Chicago , MIN-MAX HEAP AND DEAP DATA STRUCTURE A Research Report on MIN MAX HEAP AND DEAP DATA STRUCUTRE, February, 2014, MIN MAX HEAP AND DEAP DATA STRUCUTRE