پارادوکس‌های زنون

پارادوکس‌های زنون (به انگلیسی: Zeno's paradoxes) مجموعه‌ای از مسئله‌های فلسفی است که توسط زنون الئایی (حدود ۴۹۰–۴۹۵ پ. م در الئا جنوب ایتالیای کنونی- حدود ۴۳۰ پ. م) فیلسوف یونانی طراحی شده‌است. این پارادوکس‌ها در ادامه نظریه پارمنیدس که منکر نقش حواس در شناخت و تکثرگرایی است و اعتقاد به اینکه حرکت چیزی جز توهم نیست، می‌باشند؛ که زنون بر اساس دیالکتیک پارمنیدسِ افلاطون این پارادوکس‌ها را طراحی نموده‌است که در حقیقت جوابی است برای فیلسوف‌هایی که در مخالفت با پارمنیدس پارادوکس‌هایی را مطرح کرده‌اند.

داستان آشیل و لاک پشت
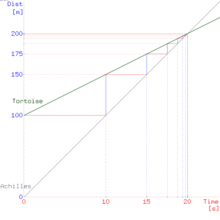
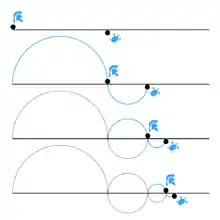
مسافت و زمان با فرض اینکه سرعت لاکپشت نصف سرعت آشیل می‌باشد
آشیل و لاکپشت

آشیل تصمیم می‌گیرد با یکی از کندترین رقبای خود، لاک پشت، مسابقهٔ دو بدهد. او لطف می‌کند و می‌گذارد لاک پشت از نقطه ای جلوتر از او مسابقه را شروع کند. وقتی آشیل از نقطهٔ شروع خود حرکت می‌کند، لاک پشت قبلاً یک مسافتی پیش رفته‌است و مدتی طول می‌کشد، البته نه خیلی زیاد، تا آشیل به نقطه ای برسد که لاک پشت حرکتش را از آن جا شروع کرده‌است مسلماً تصور می‌کنیم آشیل، تیزپاترین دونده در میان یونانیانِ اعزام شده به تروا، بیش از این عقب نخواهد ماند: هر چقدر هم مسیر مسابقه کوتاه و فاصلهٔ اولیهٔ لاک پشت از آشیل زیاد باشد، آشیل باید زودتر به خط پایان برسد. اما در واقع این‌طور نیست؛ زیرا مدتی طول می‌کشد تا آشیل به نقطه ای برسد که لاک پشت از آن جا راه افتاده، و لاک پشت در این مدت خود را کمی جلو کشانده اشت. زمانی که آشیل به آن نقطه برسد، لاک پشت جلوتر است. پس آشیل به سمت نقطه ای می‌دود که لاک پشت از آن جا راه افتاده و لاک پشت در این مدت خود را کمی جلو کشانده‌است. زمانی که آشیل به آن نقطه برسد، لاک پشت جلوتر است پس آشیل به سمت نقطه ای می‌دود که لاک پشت هم اینک هست و مدتی طول می‌کشد تا به آن نقطه برسد. مسلماً در طول این مدت لاک پشت باز کمی دیگر خود را جلو کشانده‌است. آشیل مثل سایه لاک پشت را تعقیب می‌کند، اما زمانی که به نقطه ای می‌رسد که لاک پشت بوده، لاک پشت باز هم اندکی جلو رفته‌است و آشیل هنوز به او نرسیده‌است این ماجرا تا ابد ادامه می‌یابد، زیرا همواره مدتی طول می‌کشد تا آشیل فاصلهٔ میان خودش و لاک پشت را طی کند، و هر قدر هم که لاک پشت کند حرکت کند بخشی از مسافت را در زمان حرکت خود طی می‌کند و دیگر در نقطهٔ قبل نیست و از آن نقطه جلوتر است. پس به هر حال هر چقدر هم این زنجیره را ادامه دهیم، آشیل هرگز به لاک پشت نمی‌رسد، چه رسد به این که از او جلوتر بزند. پس مسلماً وقتی که مسابقه در نهایت به پایان می‌رسد، لاک پشت از آشیل جلوتر است.

این پارادوکس نشان می‌دهد که ما نه تنها نمی‌توانیم به دوندهٔ کندتر از خودمان برسیم، بلکه اصلاً نمی‌توانیم در استادیوم بدویم.[1]

تناقض دو بخشی

آنچه که در حرکت است باید قبل از رسیدن به هدف به نیمه راه برسد.[2]

تقسیم دوبخشی در دو حالت

نتیجه حاصل می‌تواند به صورت زیر نمایش داده شود:

اگر از نقطهٔ A به نقطهٔ B بدوید، قبل از رسیدن به B باید از نقطهٔ میانی این مسافت عبور کنید. پس از این نقطهٔ میانی، باید از نقطهٔ میانی دیگری بگذرید که قبل از B به آن برسید. در واقع بی‌نهایت نقطه میانی قبل از رسیدن به B وجود دارد. پس هرگز به خود نقطهٔ B نمی‌رسید، زیرا هر بار که هر یک از مسافت‌های کاهش یابنده را به قصد نقطهٔ میانی بعدی طی می‌کنید هنوز فاصله‌ای به همان اندازه باقی مانده‌است که باید پیموده شود، و این فاصله هرگز به صفر نمی‌رسد، همیشه میان شما و انتهای مسیر فاصله‌ای وجود دارد و در نتیجه رسیدن به نقطهٔ پایان غیرممکن است. البته به فرض این که اصلاً بتوانید حرکتتان را شروع کنید. اما اصلاً چطور می‌توانید حرکتتان را شروع کنید؟ زیرا قبل از رسیدن به میانهٔ مسیر باید یک‌هشتم مسیر را بدوید و پیش از آن یک شانزدهم مسیر را، و همین‌طور تا بی‌نهایت. هیچ حرکت آغازینی وجود ندارد، زیرا همیشه قبل از آن حرکت دیگری هست که باید اول انجامش داد.

نتایج دو پارادوکس زنون به نظر بی‌معنی می‌آید، و اتفاقاً نکتهٔ قضیهٔ هم دقیقاً همین است. اگر ما نتوانیم نتیجه را قبول کنیم باید چیز دیگری را رد کنیم، مثلاً یکی از فرض‌هایی را که به نتیجه منتهی شده‌است. در این صورت استدلال از الگوی برهان خلف پیروی می‌کند؛ الگویی که به نظر می‌رسد زنون آن را تکمیل کرده‌است. اساس کار این الگو آن است که نشان می‌دهد اگر فرضی را بپذیرید (که باید خلاف آن ثابت شود) نتیجه ای بی‌معنی و نپذیرفتنی به دست می‌آید، و بهترین راه رفع این بی‌معنایی رد کردن فرض اولیه است.

پارادوکس پیکان
پارادوکس پیکان

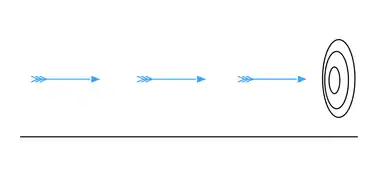
همه چیزهایی که فضای مساوی را اشغال می‌کنند در حالت استراحت هستند و آنچه در حرکت است و همیشه در هر لحظه این فضا را اشغال می‌کند، بنابراین پیکان رها شده بی حرکت است.[3]

در پارادوکس پیکان زنون بیان می‌کند که حرکت یعنی تغییر دادن فضای اشغال شده یک شی. برای مثال یک تیر را پرتاب می‌کند. او می‌گوید در هر لحظه‌ای (حتی کوتاهترین زمان) پیکان هیچ حرکتی ندارد.[4] پیکان نه به مکانی که هست می‌تواند حرکت کند و نه به مکانی که نیست؛ زیرا در مکانی که هست حرکت نکرده، و به جایی که نیست زمانی برای حرکت به آنجا وجود ندارد. به عبارت دیگر در هر لحظه‌ای از زمان هیچ حرکتی رخ نداده. اگر هر چیزی در هر لحظه بی حرکت باشد، و زمان کاملاً متشکل از لحظات باشد، پس حرکت غیرممکن است. در حالی که دو پارادوکس اول مکان را تقسیم می‌کنند، در این پارادوکس با تقسیم زمان (نه به بخش‌ها، بلکه به نقاط) بیان می‌شود.[5]

ردیف‌های متحرک
ردیف‌های متحرک

ما باید پیش خود سه دسته جسم در یک ورزشگاه یا میدان مسابقه تصور کنیم. یک دسته ساکن است، دو دسته دیگر در جهات مخالف یکدیگر با سرعت مساوی در حرکتند. در رسیدن به وضع مساوی ب۱ از نیمی از اجسام دسته الف عبور کرده‌است، در حالیکه مقدمه ج۱ از همه اجسام دسته ب عبور کرده‌است. اگر یک واحد طول در یک واحد زمان طی شود، پس مقدمه ب۱ نصف زمانی زا گرفته‌است که مقدمه ج۱ برای رسیدن به وضع مساوی گرفته‌است. از سوی دیگر مقدمه ب۱ از همه اجسام دسته ج گذشته‌است، درست همان گونه که مقدمه ج۱ از همه اجسام دسته ب عبور کرده‌است؛ بنابراین زمان عبور آن‌ها باید مساوی باشد. پس ما به نتیجه محالی رسیده‌ایم که نصف یک زمان معین مساوی تمام آن زمان است.[6]

انتقادها

برخی معتقدند زنون با طرح این پارادوکس‌ها در تلاش برای قانع کردن ما بوده که حرکت غیرممکن است؛ یعنی ما باید این نتیجهٔ ظاهراً بی‌معنی را بپذیریم که هرگز نمی‌توانیم از نقطهٔ A تکان بخوریم، زیرا اصلاً حرکت وجود ندارد. پارمنیدس قبلاً تلاش کرده بود ما را دراین باره قانع کند و پارادوکس‌های زنون دربارهٔ حرکت را اغلب ادامهٔ آن تلاش‌ها برای رسیدن به همان نتیجه تلقی می‌کنند.

اما حتی اگر زنون از طرح این پارادوکس‌ها چنین هدفی را دنبال می‌کرده، باید گفت که خود آن‌ها ساختار برهان خلف را ندارند. در برهان خلف به جای آن که فرضیه‌ها را بپذیریم و نتیجه را کاملاً قبول کنیم، باید ناچار شویم نتیجهٔ بی‌معنی را رد کنیم، و بنابراین در درستی قضیه‌هایی که این نتیجه از آن‌ها قرار گرفته شده‌است تردید کنیم. فرض کنید ما نتیجهٔ بی‌معنی آن‌ها را راحت قبول نکنیم. فرض کنید بگوییم این که آشیل هرگز از لاک پشت جلو نمی‌زند و این که دونده هرگز به نقطهٔ پایان مسابقه نمی‌رسد نمی‌توانند صادق باشند. آن وقت چه می‌شود؟ در آن صورت باید فرضی را که استدلال را به آن نتیجه رسانده رد کنیم. برخی صاحب نظران معتقدند که هدف او تقسیم نامتناهی زمان و مکان بوده‌است. ما می‌توانیم کاملاً مطمئن باشیم که زنون مایل بود ثابت کند که کثرت غیرممکن است؛ او به پیروی از پارمنیدس معتقد بود که ممکن نیست بیش از یک چیز در جهان وجود داشته باشد. او در این دو پارادوکس نتیجه‌ای عجیب را خلق می‌کند، به این ترتیب که این تصور را القا می‌کند که هر چقدر هم بخشی از زمان یا مکان مفروض شما کوچک باشد، همیشه می‌توانید آن را به بخش‌های کوچک‌تری تقسیم کنید. دونده هر قدر هم به پایان مسابقه نزدیک شود، همواره نیمی دیگر از مسافت باقی است که باید طی شود و آن نیم دیگر را هم می‌توان به دو نیم دیگر تقسیم کرد، الی آخر. از آن جا که این زنجیرهٔ تقسیم‌ها، یعنی به دو نیمه تقسیم کرد، الی آخر.

این نتیجه صادق است و از این قضیه استنتاج می‌شود که مکان‌ها را پیوسته فرض کنیم که به لحاظ نظری تا بینهایت تقسیم‌پذیر است. امروزه ما عموماً معتقدیم مکان (به لحاظ ریاضی) حالت پیوسته دارد، اگر چه به لحاظ فیزیکی نمی‌توان خطوط یا نقاطی را [تا بی‌نهایت] رسم کرد که آن خطوط یا نقاط با هم تداخل نداشته باشند. در نظریهٔ ریاضی هیچ حدی برای تقسیم کردن پاره خط وجود ندارد. همین فرض است که سبب این تصور می‌شود که به پایان رساندن مسیر مسابقه ناممکن است، زیرا هیچ مرحلهٔ آخری وجود ندارد. پس شاید زنون می‌خواسته ما به این نتیجه برسیم که تقسیم‌های بی‌نهایتِ مکان ناممکن است. مخالفان از زمان ارسطو به بعد غالباً خاطرنشان کرده‌اند که با پذیرفتن این که زمان هم دقیقاً مانند مکان تا بی‌نهایت تقسیم پذیر است، می‌توان پارادوکس آشیل را حل کرد. اما پارادوکس دوم نشان می‌دهد که پاسخ به این سادگی‌ها نیست، زیرا در پارادوکس دوم ما فرض می‌کنیم که زمان، مانند مکان، تا بی‌نهایت تقسیم‌پذیر است، و اصلاً با این فرض است که پارادوکس ادامه می‌یابد. هر چقدر هم‌زمان کوتاهی طول بکشد که آشیل فاصلهٔ میان خودش و لاک پشت را طی کند، آن زمانِ کوتاه باز بخشی از زمان است و آن قدر هست که لاک پشت از جای قبلی خود جنبیده باشد. در هیچ نقطه ای زمان تمام نمی‌شود: ما همیشه می‌توانیم آن را به زمان‌های کوتاه‌تر تقسیم کنیم و بفهمیم که لاک پشت وقت دارد که دوباره جلو بیفتد. به این ترتیب منطقی است که پارادوکس اول و دوم را یک جفت استدلال ببینیم که اولی ساده‌تر و دومی پیچیده‌تر است، اما بی‌معنایی هر دو ناشی از تقسیم بی‌نهایتِ زمان و مکان است.[7]

در پارادوکس اول هر چقدر هم به فاصله‌های ریزتر تقسیم شود، فاصله‌ای متناهی باقی می‌ماند و می‌توان آن را در زمانی متناهی طی کرد؛ زیرا دونده، در زنجیرهٔ فاصله‌های کاهش یابنده، هر پاره‌ای از مسافت را در زمان کوتاه‌تری نسبت به پارهٔ بزرگ‌تر قبلی طی می‌کند، و همین‌طور که مسافت‌ها کوچک و کوچکتر می‌شوند تا این که محو شوند، زمان لازم برای پیمودن آن‌ها نیز کوچک و کوچک‌تر می‌شود تا این که محو شود؛ در هر دو مورد جمع کل مجموعهٔ اجزاء، اگر آن‌ها را با هم جمع کنیم، برابر همان مسافت و زمان می‌شود که ما پیش از انجام عملِ تقسیم داشتیم. در ریاضیات تکنیک‌هایی برای محاسبهٔ مجموع یک زنجیرهٔ نامتناهی وجود دارد، اما ساده‌ترین برهان این است که خیلی راحت مسئله را در مکان تصویر کنیم. ریاضیدانان ممکن است بگویند پارادوکس‌های زنون فقط به این سبب ادامه می‌یابند که او برخی حقایق روشن ریاضی را متوجه نشده‌است و بنابراین اصلاً لازم نیست فرضی را که زنون امیدوار بود هدف تجدید نظر ما باشد هدف قرار دهیم. بنیان پارادوکس زنون بر تقسیم مداوم به تکه‌های کوچک و کوچک‌تر است؛ تقسیم کردنی که در محدودهٔ بخشی متناهی از زمان و مکان، میان لحظهٔ شروع مسابقه و لحظه ای که آشیل به لاک پشت می‌رسد - درست پیش از آن که از او جلو بزند - انجام می‌شود. در انتهای آن بخش از مسابقه به هر حال نقطهٔ عبوری وجود دارد و می‌توانیم محاسبه کنیم که آن نقطه کی پدیدار می‌شود.

ریاضیات می‌تواند با ارائه برهان‌هایی اثبات کند که انواع خاصی از زنجیره‌های نامتناهی که به صفر میل می‌کنند دارای مجموع متناهی‌اند و مبنای پارادوکس زنون چنین زنجیره‌هایی است. از آن جا که مجموع اجزا متناهی و سرعت پیش روی ثابت است، زمانی که برای انجام این کار طول می‌کشد باید متناهی باشد. به این ترتیب پارادوکس‌ها حل می‌شوند. بنیان پارادوکس زنون بر تقسیم مداوم به تکه‌های کوچک و کوچک‌تر است؛ تقسیم کردنی که در محدودهٔ بخشی متناهی از زمان و مکان، میان لحظهٔ شروع مسابقه و لحظه ای که آشیل به لاک پشت می‌رسد - درست پیش از آن که از او جلو بزند - انجام می‌شود. در انتهای آن بخش از مسابقه به هر حال نقطه‌ای عبوری وجود دارد و می‌توانیم محاسبه کنیم که آن نقطه کی پدیدار می‌شود. پس ریاضیات می‌تواند با ارائه برهان‌هایی اثبات کند که انواع خاصی از زنجیره‌های نامتناهی که به صفر میل می‌کنند دارای مجموع متناهی‌اند و مبنای پارادوکس زنون چنین زنجیره‌هایی است. از آن جا که مجموع اجزا متناهی و سرعت پیش روی ثابت است، زمانی که برای انجام این کار طول می‌کشد باید متناهی باشد. به این ترتیب پارادوکس‌ها حل می‌شوند.

در پارادکسی که برای اندازه‌گیری حرکت پیکان می‌باشد باید ببینیم آیا در مجاورت چیزی به اندازهٔ خودش هست یا نه، اما جایی را که پیکان در فضا اشغال می‌کند نمی‌توان معیاری برای نشان دادن نمودار حرکت آن در نظر گرفته شود، زیرا پیکان همواره جایی به اندازهٔ خودش اشغال می‌کند. پیکان هرگز از جای خودش فراتر نمی‌رود و بنابراین، با این معیار سکون، به نظر می‌رسد که در تمام مدت حرکت خود ساکن است.

جستارهای وابسته

منابع
  1. تاریخ فلسفه کاپلستون جلد اول
  2. فیزیک نوشته ارسطو
  3. فیزیک، ارسطو
  4. زندگی و عقاید فیلسوفان برجسته اثر دیوگنیس لائرتیوس
  5. دانشنامه فلسفه استنفورد بخش پارادوکس پیکان زنون
  6. تاریخ فلسفه کاپلستون جلد اول ترجمه جلال الدین مجتبوی
  7. آزبورن، کاترین؛ فلسفه پیش سقراطی برگردان گلناز صالح کریمی، تهران: نشر ماهی، چاپ اول

پیوند به بیرون
متن مربوطه در ویکی‌نبشته: Zeno of Elea
  • Dowden, Bradley. "Zeno’s Paradoxes." Entry in the دانشنامه اینترنتی فلسفه.
  • Introduction to Mathematical Philosophy, Ludwig-Maximilians-Universität München
  • Silagadze, Z. K. "Zeno meets modern science,"
  • Zeno's Paradox: Achilles and the Tortoise by Jon McLoone, Wolfram Demonstrations Project.
  • Kevin Brown on Zeno and the Paradox of Motion
  • Palmer, John (2008). "Zeno of Elea". Stanford Encyclopedia of Philosophy.
  • This article incorporates material from Zeno's paradox on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
  • Grime, James. "Zeno's Paradox". Numberphile. Brady Haran. Archived from the original on 3 October 2018. Retrieved 17 December 2016.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.