پروفر کد

در ریاضیات ترکیبیاتی، کدِ پروفر (دنبالهٔ پروفر یا اعداد پروفر) برای یک درخت برچسب‌دار، یک دنباله از اعداد است که به این درخت نسبت داده می‌شود. طول این دنباله برای یک درخت n رأسی دقیقاً n-2 است، و می‌توان آن را با یک الگوریتم تکرار شونده ساده تولید کرد. پروفر کد برای اولین بار به وسیلهٔ هینز پروفر برای اثبات فرمول کیلی استفاده شد.[1]

الگوریتم تبدیل یک درخت به کد پروفر

یک درخت با کد پروفر 4،4،4و5 (از راست به چپ)

کد پروفر برای یک درخت می‌تواند با حذف کردن پی در پی رأس‌های یک درخت تا وقتی که تنها ۲ رأس مانده، به دست آید. یعنی اگر T یک درخت برچسب‌دار با رأس های ${\displaystyle \{1,2,...,n\}}$ باشد، در مرحلهٔ iام کوچک‌ترین برگ درخت را حذف کرده و شمارهٔ همسایهٔ آن را به عنوان عنصر iام کد قرار می‌دهیم.
کد پروفر برای یک درخت برچسب‌دار یکتاست و دقیقاً n-2 عنصر دارد.

یک مثال

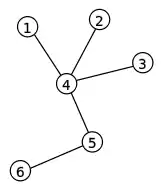
فرض کنید الگوریتم بالا بر روی درخت سمت چپ اجرا شود. در ابتدا رأس شمارهٔ 1 برگی است که کوچک‌ترین شماره را بین برگ‌ها دارد، از این رو این برگ اول از همه پاک می‌شود و عدد 4(شمارهٔ رأس متصل به 1) در کد پروفر قرار می‌گیرد. سپس رأس‌های 2 و 3 حذف می‌شوند، پس 4 دو بار دیگر نیز به کد اضافه خواهد شد. در این حال رأس 4 کوچک‌ترین برگ در درخت است و در نتیجه ما 4 را نیز حذف می‌کنیم و شمارهٔ 5 را به دنباله اضافه می‌کنیم. تنها 2 رأس باقی‌مانده پس فرایند متوقف خواهد شد.

الگوریتم تبدیل یک کد پروفر به درخت

فرض کنید ${\displaystyle \{a[1],a[2],...,a[n]\}}$ یک کد پروفر باشد.
درخت حاصل n+2 رأس، با شماره‌های 1تاn+2 خواهد داشت. درجه را برای هر رأس یکی بیشتر از تعداد بارهای ظاهر شدن آن در دنبالهٔ پروفر قرار دهید. برای مثال به صورت شبه کد:

  Convert-Prüfer-to-Tree(a)
  1 n ← length[a]
  2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2
  3 degree ← an array of integers
  4 for each node i in T
  5     do degree[i] ← 1
  6 for each value i in a
  7     do degree[i] ← degree[i] + 1

سپس برای هر رأس در ${\displaystyle a[i]}$ ، کوچک‌ترین رأس j با درجهٔ 1 را پیدا کنید و با اضافه کردن یال (j,${\displaystyle a[i]}$) به درخت از درجهٔ این دو رأس یک واحد کم کنید. به صورت شبه کد:

  8 for each value i in a
  9     for each node j in T
 10          if degree[j] = 1
 11             then Insert edge[i, j] into T
 12                  degree[i] ← degree[i] - 1
 13                  degree[j] ← degree[j] - 1
 14                  break

در انتهای حلقه دو رأس با درجهٔ یک باقی می‌ماند(فرض کنیدvوu) در پایان یال (v,u) را به درخت اضافه کنید.[2]

 15 u ← v ← 0
 16 for each node i in T
 17     if degree[i] = 1
 18         then if u = 0
 19             then u ← i
 20             else v ← i
 21                  break
 22 Insert edge[u, v] into T
 23 degree[u] ← degree[u] - 1
 24 degree[v] ← degree[v] - 1
 25 return T

فرمول کلی

واضح است که پروفر کد یک درخت برچسب‌دار، یک دنباله به طول n-2 یکتا است. اما این که برای هر دنباله به طول n-2 از اعداد 1 تا n یک درخت برچسب‌دار یکتا وجود دارد آنقدر واضح نیست.
نتیجهٔ مستقیم این عبارت این است که کد پروفر، یک تابع یک به یک و پوشا بین مجموعهٔ درخت‌های n رأسی برچسب‌دار و مجموعهٔ دنباله‌هایی به طول n-2 از اعداد 1 تا n ارائه می‌دهد. مجموعهٔ دوم ${\displaystyle n^{n-2}}$ عضو دارد، پس وجود این تابع یک به یک و پوشا فرمول کیلی را اثبات می‌کند: تعداد درخت‌های n رأسی برچسب‌دار برابر با ${\displaystyle n^{n-2}}$ است.

کاربردهای دیگر

• فرمول کیلی می‌تواند تعمیم داده شود تا ادعای زیر را ثابت کند:

تعداد درخت‌های پوشا با درجه‌های ${\displaystyle d_{1},d_{2},...,d_{n}}$ در یک گراف کامل n رأسی(${\displaystyle K_{n}}$) برابر است با

${\displaystyle {\binom {n-2}{d_{1}-1,\,d_{2}-1,\,\dots ,\,d_{n}-1}}={\frac {(n-2)!}{(d_{1}-1)!(d_{2}-1)!\cdots (d_{n}-1)!}}.}$

زیرا در پروفر کد این درخت‌ها عدد i دقیقاً ${\displaystyle d_{i}}$ بار آمده‌است.

• فرمول کیلی می‌تواند به این صورت نیز تعمیم داده شود:

یک درخت برچسب‌دار در حقیقت یک درخت پوشا در گراف کامل برچسب‌دار متناظر است. همچنین با گذاشتن محدودیت‌هایی بر روی کدهای پروفر شمرده شده،به روشی مشابه می‌توان تعداد درخت‌های پوشای یک گراف دو بخشی کامل را نیز به دست آورد. اگر گراف کامل 2 بخشی G از دو بخش به ترتیب ${\displaystyle n_{2}}$و${\displaystyle n_{1}}$ رأسی تشکیل شده باشد(${\displaystyle n=n_{1}+n_{2}}$)، تعداد درخت‌های پوشای برچسب‌دار G برابر است با ${\displaystyle n_{1}^{n_{2}-1}n_{2}^{n_{1}-1}}$

• تولید دنباله‌های تصادفی پروفر با احتمال مساوی و تبدیل آن‌ها به درخت برچسب دار یکی از راه‌های سادهٔ تولید درخت‌های برچسب دار تصادفی با احتمال مساوی است.

منابع

1. Prüfer, H. (1918). "Neuer Beweis eines Satzes über Permutationen". Arch. Math. Phys. 27: 742–744.
2. Jens Gottlieb, Bryant A. Julstrom, Günther R. Raidl, and Franz Rothlauf. (2001). "Prüfer numbers: A poor representation of spanning trees for evolutionary search" (PDF). Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001): 343–350. Archived from the original (PDF) on 26 September 2006. Retrieved 20 May 2014.

پیوند به بیرون

• Prüfer code – from MathWorld