پلانی‌متر

Sathŝomār(به انگلیسی: Planimeter) (که به آن پلاتو متر نیز گفته می‌شود) یک وسیله اندازه‌گیری است که برای تعیین مساحت یک شکل دو بعدی دلخواه استفاده می‌شود. ساختمان دستگاه چند نوع دستگاه مساحت سنج وجود دارد اما تمام این‌ها به یک روش عمل می‌کنند روش دقیقی که این دستگاه‌ها ساخته شده‌اند متفاوت است. نوع اصلی این دستگاه که مکانیکی است ممکن است پلار (قطبی)خطی یا نوک تیز باشد. ریاضی‌دان سوییسی به نامjakobamsler-laffonمساحت سنج را در سال 1854ساخت که بر اساس نظرmartinhermanjohann در سال1814 بود. بعد از ساخت اولین مساحت سنج مساحت سنج‌های تکامل یافته دیگری ساخته شدند که امروزه نوع الکترونیک آن وجود دارد .

  نمونه پلانی متر قطبی
  پلانی متر قطبی

' مساحت سنج (۱۹۰۸) اندازه‌گیری مساحت مشخص با ردیابی محیط آن

پلانی متر امسلر

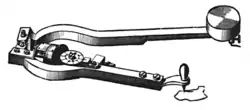
در دستگاه‌های مساحت سنج یک بازوی رابط با یک سوزن نقطه گذار در یک طرف قرار دارد که بر اثر حرکت در اطراف شکل مورد نظر علائمی را به جا میگذارد . در قسمت دیگر دستگاه بازویی قرار گرفته که در مساحت سنج قطبی منحصراً به صورت خطی عمل می‌کند . در این دستگاه وقتی که یک بازو در اطراف سطح مورد نظر حرکت می‌کند در قسمت دیگر دستگاه مساحت شکل مورد نظر مشخص می‌شود این دستگاه دارای یک چرخ است که همراه با حرکت قسمت نقطه گذار دستگاه شمارش می‌کند . زمانی که چرخ دستگاه به صورت عمود بر محور حرکت می‌کند می چرخد و این حرکت ثبت می‌شود.زمانی که چرخ دستگاه موازی محور خود حرکت می‌کند چرخ‌ها لیز می خورند و نمی‌چرخند و این حرکت ثبت نمی‌شود .این بدین معنی است که در دستگاه مساحت سنج هر مسیری که چرخ آن حرکت می‌کند اندازه‌گیری می‌شود . در واقع حرکت‌های عمود بر محور چرخش تعیین‌کننده مساحت توسط دستگاه است . مساحت شکل متناسب است با تعداد دفعاتی که چرخ دستگاه چرخش می‌کند .

یک نوع پلانی متر خطی برای تعیین مساحت شکل‌های کشیده

پیشرفت دستگاه می‌تواند بر استقرار موقعیت اولین نقطه سطح ( مرکز سطح ) و حتی بر دومین نقطه اثر بگذارد . در تصاویر مساحت سنجخطی و قطبی دیده می‌شود .

مساحت سنج خطی
مساحت سنج قطبی

نقطهٔ M ) ) در یک طرف دستگاه مساحت سنج نقطهٔ ( C ) و شمارش گر سطح S))را دنبال می‌کند تا به نقطهٔ آخر برسد . در مساحت سنج خطی حرکت بازوی (E) منحصراً روی محور y است. در مساحت سنج قطبی بازو به بازوی دیگری متصل است که در نقطهٔ آخر یعنیO متصل می‌شود . اتصال به بازویME همان اندازه‌گیری چرخ است که چرخ دور محور خودش به موازاتMEحرکت کرده‌است و این باعث می‌شود چرخ لیز بخورد بدون محاسبهٔ سطح .

اساس کار مساحت سنج خطی کار یک مساحت سنج خطی بر اساس اندازه‌گیری یکمستطیل ABCDدر تصویر توضیح داده می‌شود .

اساس کار مساحت سنج خطی

حرکت قسمت علامت گذار از نقطهٔ A به B بازوی ME در ضمن صفحهٔ زرد رنگ حرکت می‌کند . مساحتی مساوی با PQ × EM محاسبه می‌شود. این مساحت مساوی است با مساحت صفحهٔ A"ABB" . چرخدستگاه فاصلهٔ بینPQ را اندازه‌گیری می‌کند کهعمود بر EM است. با حرکت از نقطه یC به DبازویEM در ضمن صفحهٔ سبز رنگ حرکت می‌کند . (مساحتی مساوی با سطح مستطیلD"DCC.) چرخ دستگاه در جهت عکس حرکت می‌کند و سطح محاسبه شده را از سطح قبلی کسر می‌کند . نتیجهٔ نهایی اندازه‌گیری بین سطح زرد و سبز می‌باشد که در واقع اندازه مستطیلABCDاست . که در واقع حرکت در طولBC و DA است . هر دو اندازه یکی هستند اما در جهت مخالف که حرکت چرخ آن‌ها را حذفمی نماید.

محاسبات ریاضی عملکرد یک پلانی متر خطی می‌تواند توسط به کارگیری تئوریGreen's روی اجزای بردار سطحN توجیه شود. داریم :

جایی که b هم پایهٔ yاست در زانویی E این بردار سطح عمود بر بازوی اندازه‌گیری EM است :

و اندازه ثابتی دارد برابر طول mاز بازوی اندازه‌گیری:

سپس:

زیرا :

سمت چپ تساوی بالا که مساوی مساحتسطح بستهٔ A بوسیلهٔ خطوط خارجی است طول بازوی اندازه‌گیری شده متناسب است با فاصلهٔ اندازه‌گیری شده با اندازه‌گیری چرخشی و با فاکتور نسبی m مختصات قطبی ارتباط تئوری Green's در ترم‌های منسجم مختصات قطبی می‌تواند فهمیده شود در مختصات قطبی بازو توسط انتگرال تولید می‌شود و جایی که شکل کامل می‌شود معادلهٔ درجه دومی به عنوان ضریب rوجود دارد به این معنا که به ازا زوایای مختلف نسبت مساحتی که تغییر می‌کند با توان دوم زوایا در شعاع متناسب است. برای یک تساوی پارامتریک در مختصات قطبی جایی کهr و θتابعی از زمان هستند داریم :

چرخیدن پلانی متر برای هر چرخی که در انتهای خط ثابت شده و حول آن می چرخد به ترتیب با هر نقطهٔ چرخش نهایی چرخ متناسب است با انتگرال و متناسب است با مسافت طی شده در هر نقطه که در هر زمان به شعاع بستگی دارد و در اطراف دایره با زاویه تغییر می‌کند .

 این ضرب داخلی را با مشتق گرفتن از انتگرال اولیه  می‌توان بدست آورد که نشان می‌دهد یک پلانی متر سطح انتگرال را تولید می‌کندکه طبق تئوری Green'sانتگرال خطی یک تابع درجه یک تا درجه دوی معین است.

اصل پلانی متر خطی

اصل پلانی متر خطی

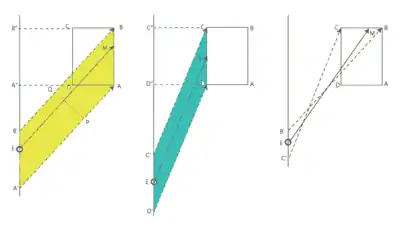
می‌توان طرز کار پلانی متر خطی را با اندازه‌گیری مساحت مستطیل ABCD توضیح داد (تصویر را ببینید). حین حرکت اشاره گر از A به B بازوی EM روی متوازی‌الأضلاع زرد با مساحتی برابر PQ*ME حرکت می‌کند. این مساحت همچنین با مساحت متوازی‌الأضلاع A"ABB" برابر است. دور شمار فاصله PQ را اندازه‌گیری می‌کند (عمود بر EM). در حرکت از C به D بازوی EM متوازی الضلاع سبز را طی می‌کند که مساحتی برابر با مساحت مستطیل D"DCC" دارد. حالا دور شمار در جهت عکس حرکت می‌کند (کم کردن این مقدار از مقدار قبلی). نتیجه نهایی اندازه‌گیری اختلاف مساحت متوازی‌الأضلاع زرد و سبز که همان ناحیهٔ ABCD است، می‌باشد. همچنین حرکتی در طول BC و DA وجود دارد اما چون برابر و در خلاف جهت هم اند، یکدیگر را در خواندن عدد گردنده خنثی می‌کنند.

منشا ریاضی

عملکرد پلانی متر خطی با استفاده از قضیهٔ گرین بر روی اجزای میدان برداری N توجیه می‌شود. توسط:

${\displaystyle \!\,N(x,y)=(b-y,x),}$

جایی که b مختصات جهت y از زانوی E است. این میدان برداری بر بازوی اندازه‌گیری EM عمود است:

${\displaystyle {\vec {EM}}\cdot N=xN_{x}+(y-b)N_{y}=0}$

و دارای اندازه ثابتی برابر با طول m از بازوی اندازه‌گیری است:

${\displaystyle \!\,\|N\|={\sqrt {(b-y)^{2}+x^{2}}}=m}$

بنابر این:

${\displaystyle \oint _{C}(N_{x}dx+N_{y}dy)=\iint _{S}\left({\frac {\partial N_{y}}{\partial x}}-{\frac {\partial N_{x}}{\partial y}}\right)dxdy=}$

${\displaystyle =\iint _{S}\left({\frac {\partial x}{\partial x}}-{\frac {\partial (b-y)}{\partial y}}\right)dxdy=\iint _{S}dxdy=A,}$

چون:

${\displaystyle {\frac {\partial }{\partial y}}(y-b)={\frac {\partial }{\partial y}}{\sqrt {m^{2}-x^{2}}}=0,}$

طرف چپ تساوی بالا، که با ناحیهٔ احاطه شده توسط منحنی بسته (A)برابر است، با فاصله اندازه‌گیری شده توسط گردنده اندازه‌گیری متناسب است(با فاکتور تناسب m-طول بازوی اندازه‌گیری.)

مختصات قطبی

ارتباط با قضیه گرین از دیدگاه یکپارچه سازی در دستگاه مختصات قطبی قابل درک است. در دستگاه مختصات قطبی، مساحت ازانتگرال ${\displaystyle \scriptstyle \int _{\theta }{\tfrac {1}{2}}r(\theta )^{2}\,d\theta ,}$ محاسبه می‌شود، وقتی فرم یکپارچه می‌شود درجه r است، به این معنی که نرخ در هر ناحیه با توجه به تغییر در درجه تفاوت زاویه با شعاع تغییر می‌کند. برای یک معادله پارامتری در دستگاه قطبی، جایی که rو a به صورت تابعی از زمان تغییر کنند، خواهیم داشت:

${\displaystyle \int _{t}{\tfrac {1}{2}}r(t)^{2}d(\theta (t))=\int _{t}{\tfrac {1}{2}}r(t)^{2}\cdot {\dot {\theta }}(t)\,dt.}$

در پلانی متر برای چرخی که به انتهای اتصال ثابت شده‌است و حول یک نقطه می‌چرخد، کل گردش چرخ با ${\displaystyle \scriptstyle \int _{t}r(t)\cdot {\dot {\theta }}(t)\,dt,}$ متناسب است، همچنین گردش با مسافت پیموده شده متناسب است، که در هر نقطه از زمان با شعاع و تغییر در زاویه متناسب است، همانطور که در محیط یک دایره (${\displaystyle \scriptstyle \int r\,d\theta =2\pi r}$)است.

این جمله زیر انتگرال ${\displaystyle \scriptstyle r(t)\cdot {\dot {\theta }}(t)\,dt}$ می‌تواند به عنوان مشتق جمله زیر انتگرال قبلی${\displaystyle \scriptstyle {\tfrac {1}{2}}r(t)^{2}{\dot {\theta }}(t)\,dt}$ (نسبت به r) شناخته شود و نشان می‌دهد پلانی متر ناحیهٔ انتگرال را از دیدگاه مشتق محاسبه می‌کند، که به تئوری گرین بر می‌گردد، که با انتگرال خطی تابع در یک محیط یک بعدی به انتگرال دو بعدی مشتق معادل است.

منابع

متن مقاله‌ای مرتبط در 1911 Encyclopædia Britannica در ویکی‌نبشتهٔ انگلیسی موجود است.

• R. W. Gatterdam, The planimeter as an example of Green’s theorem, Amer. Math. Monthly 88 (1981) 701–704.
• J. L. Hodgson, Integration of flow meter diagrams, J. Sci. Instrum. 6 (1929) 116–118.
• E. M. Horsburgh Napier Tercentenary Celebration: Handbook of the Exhibition of Napier Relics and of Books, Instruments, and Devices for facilitating Calculation, The Royal Society of Edinburgh, 1914.
• G. Jennings, Modern Geometry with Applications, Springer, 1985.
• L. I. Lowell, Comments on the polar planimeter, Amer. Math. Monthly 61 (1954) 467–469.
• C. J. Sangwin and J. Bryant, How Round is your Circle, Chapter 8, Princeton University Press, 2007.
• J. Y. Wheatley, The polar planimeter, New York: Keuffel & Esser, 1908.

پیوند به بیرون

• Hatchet Planimeter
• P. Kunkel: Whistleralley site, The Planimeter
• Larry's Planimeter Platter
• Wuerzburg Planimeter Page
• Robert Foote's planimeter page
• Computer model of a planimeter بایگانی‌شده در ۶ آوریل ۲۰۰۹ توسط Wayback Machine
• Tanya Leise's planimeter explanations
• 'Tanya Leise: As the Planimeter’s Wheel Turns
• Make a simple planimeter
• O. Knill and D. Winter: ;;Green's Theorem and the Planimeter