کسر

کسر (به انگلیسی: Fraction) (از لاتین fractus به معنی "شکسته")، نمایشگر جزئی از یک کل یا به‌طور کلی تر، هر تعداد از اجزای مساوی با هم است. هنگام صحبت‌های روزمره، کسر را جهت توصیف این که چه تعداد از اجزایی با اندازه‌های مشخص وجود دارند، به کار می‌برند، مثل: یک دوم، هشت پنجم، سه چهارم. کسر رایج، متعارف یا ساده (مثال‌ها: ${\displaystyle {\tfrac {1}{2}}}$ و ${\displaystyle {\tfrac {17}{3}}}$) شامل یک صورت (Numerator) است که بالای خط قرار می‌گیرد (یا قبل از اسلش، مثل: ¹⁄₂)، و مخرج (Denominator) ناصفری که زیر آن خط قرار داده می‌شود. صورت‌ها و مخرج‌ها در کسرهایی که رایج نیستند نیز به کار می روند، انواع کسرهای غیر رایج شامل این مواردند: کسرهای مرکب، کسرهای مختلط (با اعداد مختلط اشتباه نشود)، و اعداد مخلوط.

کیکی که یک چهارم (ربع) آن برداشته شده. سه چهارم باقیمانده آن با خط چین مشخص شده و روی هر بخش را با 14 مشخص کرده‌اند.

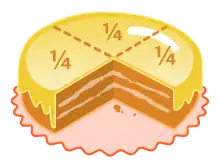
نحوه نمایش

نمایش کسر به صورت یک خط افقی و یک عدد در بالا و یک عدد در پایین می‌باشد. عدد بالایی صورت کسر و عدد پایینی مخرج کسر نامیده می‌شود.

${\displaystyle {\dfrac {2}{4}}}$

در اینجا ۲ صورت کسر و ۴ مخرج کسر می‌باشد.

در این پویا نمایی برابر کسرهای زیر نشان داده شده‌است . ${\displaystyle {\frac {1}{4}}={\frac {2}{8}}={\frac {3}{2}}={\frac {4}{16}}}$

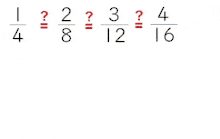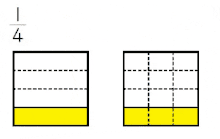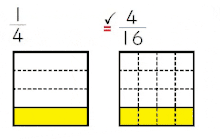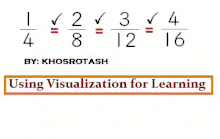
انواع کسر

کسر متعارفی

کسر متعارفی نوعی خاصی از کسر است که بنا بر تعریف، هم صورت و هم مخرج آن اعداد صحیح هستند (مخرج باید مخالف صفر باشد). به عنوان مثال، اعداد ${\displaystyle {\dfrac {4}{3}}}$ و ${\displaystyle {\dfrac {9}{6}}}$ کسر متعارفی هستند، ولی ${\displaystyle {\dfrac {4}{1.2}}}$ و ${\displaystyle 5/3/2/1}$ کسر متعارفی نمی‌باشند.

کسر بزرگتر از واحد و کوچکتر از واحد

کسر متعارفی ${\displaystyle {\dfrac {a}{b}}}$ را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم a>b، کسر از یک (واحد) بزرگتر است. در این صورت ${\displaystyle {\dfrac {a}{b}}}$ را کسر بزرگتر از واحد (Improper Fraction) می‌نامند. گاهی کسرهای بزرگتر از واحد را به صورت عدد مخلوط نشان می‌دهند.

برعکس، اگر در کسر ${\displaystyle {\dfrac {a}{b}}}$ صورت از مخرج کوچکتر باشد، یعنی a<b، کسر را کوچکتر از واحد (Proper Fraction) می‌نامند.

کسر اعشاری و درصدی

کسر اعشاری، یک کسر متعارفی است که مخرج آن ۱۰ یا توانی از ۱۰ است. اغلب برای نمایش کسرهای اعشاری از علامت ممیز (/) استفاده می‌شود. برای مثال کسر متعارفی ${\displaystyle {\dfrac {1}{10}}}$ را می‌توان به صورت ۰/۱ نشان داد. همچنین کسر ${\displaystyle {\dfrac {a}{b}}}$ را می‌توان با ضرب صورت و مخرج در مقدار ۵ به صورت ${\displaystyle {\dfrac {60}{100}}}$ یا ۰/۶۰ و حتی به طور خلاصه‌تر ۰/۶ نشان داد. کسرهای اعشاری را با نماد علمی نیز می‌توان نشان داد.

برای نمایش اعداد اعشاری که دارای بی‌نهایت رقم تکرار شونده اعشار هستند، از کسر متعارفی استفاده می‌شود. برای مثال کسر متعارفی ${\displaystyle {\dfrac {1}{3}}}$ بیانگر مقدار …۰/۳۳۳۳ است.

اگر مخرج کسر قابل تبدیل به ۱۰۰ باشد می‌توان اعداد را به صورت درصدی (Percentage) یا به صورت نماد ٪ نیز نشان داد. برای مثال کسر متعارفی ${\displaystyle {\dfrac {5}{100}}}$ همان مقدار ۵٪ است و ${\displaystyle {\dfrac {29}{100}}}$ مقدار ۲۹٪ را نشان می‌دهد.

کسر مولد اعشار مختوم

اگر با تقسیم صورت بر مخرج، به باقی‌مانده صفر برسیم، کسر را مولد اعشار مختوم می‌نامند. این حالت در زمانی رخ می‌دهد که مخرج کسر فقط شامل عامل‌های ۲ یا ۵ یا هر دو باشد.

کسر مولد اعشاری متناوب

کسرهای وجود دارند که در آن‌ها حاصل تقسیم صورت بر مخرج، باقی‌مانده صفر نخواهند داشت. به این ترتیب عدد اعشاری حاصل، مختوم نخواهد بود. برای مثال کسرهایی نظیر ${\displaystyle {\dfrac {1}{3}}}$ و ${\displaystyle {\dfrac {1}{11}}}$ یک عدد اعشاری با مقدار اعشار متناوب ایجاد می‌کنند. ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش می‌نامند. از آنجایی که مخرج این گونه کسرها دارای عامل‌های اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقی‌مانده صفر نخواهند داشت.

${\displaystyle {\dfrac {2}{3}}=0.666...}$ و ${\displaystyle {\dfrac {1}{11}}=0.090909...}$

کسر مولد اعشاری متناوب مرکب

در این گونه کسرها، با تجزیه مخرج به عوامل اول به ارقام ۲ یا ۵ و یک یا چند عدد اول دیگر می‌رسیم. در این صورت عدد اعشاری شامل دو قسمت تکراری با گردش و بدون گردش خواهد بود. برای مثال کسر ${\displaystyle {\dfrac {8}{15}}}$ از این گونه کسرها محسوب می‌شود، زیرا مخرج آن به عامل‌های ۵ و ۳ تجزیه می‌شود.

${\displaystyle {\dfrac {8}{15}}=0.5333...}$

کسرهای مخلوط و متعارف

معمولاً کسرهای متعارفی بزرگتر از ۱ را به صورت اعداد مخلوط نشان می‌دهند. در این حالت عدد مخلوط شامل یک قسمت عدد صحیح و یک کسر متعارفی کوچکتر از واحد است. قسمت عدد صحیح همان خارج قسمت تقسیم و صورت کسر، باقی‌مانده تقسیم و مخرج کسر متعارفی نیز مقسومٌ علیه خواهد بود.

${\displaystyle {\dfrac {36}{5}}=7{\dfrac {1}{5}}}$

کسر نامتعارف

اگر مخرج کسری صفر باشد، مانند ${\displaystyle {\dfrac {1}{0}}}$ آن کسر تعریف نشده است.

تاریخ پیدایش کسر متعارفی

کسر متعارفی در جریان اندازه‌گیری و زمانی پدید آمد که ناچار شدند واحد اندازه‌گیری را بشکنند؛ چرا که برای ادامه اندازه‌گیری، نتوانستند از واحد استفاده کنند. این موضوع، به ویژه از پیدایش کسرهای مشخص، پیش از پیدایش مفهوم کلی کسر، روشن می‌شود.

زمان زیادی لازم بود تا «نیم» و «یک چهارم» به صورت ۱/۲ و ۱/۴ برای هر نوع واحدی (طول، حجم، وزن، زمان) به کار رود.

در هزاره دوم پیش از میلاد بود که بشر توانست از کسر، همچون بخشی از واحد، استفاده کند. در بابل کهن، حتی نمادهای خاصی برای برخی کسرهای متعارفی وجود داشت.

گویا صفت فاعلی از مصدر گفتن می‌باشد و در ریاضی هر شمار کسری مانند و یا هر عددی که بتوان آن را به شکل یک کسر نوشت را یک عدد گویا می‌نامیم. مانند ۲-، ۰، ۳+ ،۲/۳ -، ۲۵/- که به ترتیب به شکل کسرهای می‌توان نوشت. به‌طور کلی هر عددی که بتوان آن را به صورت کسر نوشت، به‌طوری‌که صورت و مخرج آن متعلق به اعداد صحیح باشند و مخرج آن مخالف صفر باشد یک عدد گویا می‌گویند. مجموعه اعداد گویا را با حرف Q حرف اول کلمهٔ Quotient به معنی «خارج قسمت» نمایش می‌دهند.

ضرب کسر

ضرب کسر دارای انواع مختلفی است از جمله: ضرب عدد در کسر ( ضرب کسر در عدد) و ضرب کسر در کسر

ضرب عدد در کسر

ابتدا به عدد مخرج یک می دهیم و سپس صورت در صورت و مخرج در مخرج ضرب می شود. ${\displaystyle 2\times {\dfrac {9}{6}}={\dfrac {2}{1}}\times {\dfrac {9}{6}}={\dfrac {18}{6}}}$

ضرب کسر در عدد

این مورد دقیقاً شبیه ضرب عدد در کسر می باشد و ابتدا باید به عدد مخرج یک بدهیم و سپس در هم ضرب کنیم. ${\displaystyle {\dfrac {4}{5}}\times 2={\dfrac {4}{5}}\times {\dfrac {2}{1}}={\dfrac {8}{5}}}$

ضرب کسر در کسر

در این نوع ضرب صورت در صورت و مخرج در مخرج ضرب می شوند. ${\displaystyle {\dfrac {5}{7}}\times {\dfrac {9}{5}}={\dfrac {5}{7}}\times {\dfrac {9}{5}}={\dfrac {45}{35}}}$

دقت کنید در کسر های که به صورت عدد مخلوط هستند، ابتدا عدد مخلوط را به کسر تبدیل کنید و سپس ضرب را انجام دهید. ${\displaystyle 4{\dfrac {2}{3}}\times 1{\dfrac {4}{5}}={\dfrac {14}{3}}\times {\dfrac {9}{5}}={\dfrac {126}{15}}}$

تقسیم کسر

برای تقسیم دو کسر متعارفی می‌توان آن را به صورت حاصل‌ضرب نوشت و عملیات را مطابق با عملیات ضرب انجام داد. برای این کار کافی است که کسر مقسوم علیه را به صورت معکوس در آورده و در مقسوم ضرب کنیم.

${\displaystyle {\dfrac {a}{b}}\div {\dfrac {c}{d}}={\dfrac {a}{b}}\times {\dfrac {d}{c}}}$

جمع و تفریق کسر

جمع و تفریق دو کسر متعارفی با مخرج یکسان

اگر مخرج همه کسرها با هم مشابه است، صورت تمام کسرها را با هم جمع می شوند. مخرج نیز همان مخرج یکسان کسرها میباشد.

${\displaystyle {\dfrac {1}{4}}+{\dfrac {2}{4}}={\dfrac {3}{4}}}$

جمع و تفریق دو کسر متعارفی با مخرج متفاوت

دو مخرج (یا هر چند تا که هست) را در هم ضرب کرده تا مخرج مشترک به دست بیاید. اگر یکی از مخرج ها به بقیه مخرج ها بخش پذیر بود، کافی است آن مخرج به عنوان مخرج مشترک انتخاب شود. صورت ها متناسب با مخرج مشترک، بزرگ می شوند. در این حالت صورت کسرها با هم جمع می شوند.

${\displaystyle {\dfrac {1}{3}}+{\dfrac {3}{5}}={\dfrac {5}{15}}+{\dfrac {9}{15}}={\dfrac {14}{15}}}$

منابع

در ویکی‌انبار پرونده‌هایی دربارهٔ کسر موجود است.

تاریخ ریاضیات (تألیف: پرویز شهریاری)