کوچک‌ترین مضرب مشترک

در حساب و نظریه اعداد، کوچکترین مضرب مشترک (به انگلیسی: Least Common Multiple) (در متون فارسی به صورت مخفف ک. م.م. و در متون انگلیسی به صورت مخفف lcm نیز نوشته می‌شود)، از دو عدد صحیح a و b را اغلب به صورت lcm(a, b) نمایش داده که کوچکترین عدد صحیح مثبتی است که بر هردوی a و b بخشپذیر می‌باشد.[1][2][3] از آنجا که تقسیم بر صفر تعریف نشده، تعریف ک.م.م. تنها زمانی معنادار است که a و b هردو مخالف صفر باشند.[4] با اینحال، برخی از مؤلفان ${\displaystyle \operatorname {lcm} (a,0)}$ را برای تمام a‌ها برابر با صفر تعریف می‌کنند، به این دلیل که ک.م.م. را کوچکترین کران بالایی در مشبکه بخش‌پذیری تعریف می‌نمایند.

نمودار وِنی از کوچکترین مضارب مشترک ترکیبات مختلفی از ۲، ۳، ۴، ۵ و ۷ (در اینجا ۶ نادیده انگاشته شده، چرا که به صورت ۳×۲ بوده و هردوی ۲ و ۳ نیز قبلاً نمایش داده شده‌اند). به عنوان مثال، بازی ورقی را در نظر بگیرید که ورق‌های آن باید به‌طور مساوی، حداکثر بین ۵ بازیکن تقسیم شوند، در این حالت حداقل نیاز به ۶۰ ورق بازی است. همانگونه که در نمودار فوق نیز مشاهده می‌گردد، اشتراک ۲، ۳، ۴، و ۵ عدد ۶۰ بوده که در مجموعه ۷ واقع نشده.

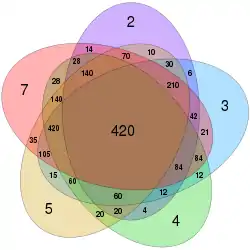
همچنین ک.م.م. «کوچکترین مخرج مشترک» (Lowest Common Denominator) (یا lcd) است که می‌توان آن را قبل از جمع، تفریق یا مقایسه کسرها به کار برد. ک.م.م. بیش از دو عدد صحیح نیز خوش‌تعریف است: در این حالت ک.م.م. برابر با کوچکترین عدد صحیح مثبتی است که بر هرکدام از آن‌ها بخش‌پذیر باشد.[2]

تعریف

فرض کنید ${\displaystyle a_{1},a_{2},...,a_{n}}$ اعدادی صحیح و ناصفر باشند. در میان مضرب‌های مشترک مثبت ${\displaystyle a_{1},a_{2},...,a_{n}}$ کوچکترین عدد را (که بنا بر اصل خوش ترتیبی وجود دارد.) کوچکترین مضرب مشترک ${\displaystyle a_{1},a_{2},...,a_{n}}$ می‌نامیم و آن را با ‍${\displaystyle [a_{1},a_{2},...,a_{n}]}$ نشان می‌دهیم.

قضیه

اگر ${\displaystyle a_{1},a_{2},...,a_{n}}$ اعدادی صحیح و ناصفر باشند، هر مضرب مشترک آن‌ها بر ${\displaystyle [a_{1},a_{2},...,a_{n}]}$ بخش‌پذیر است.

برهان: اگر ${\displaystyle k}$ مضرب مشترکی از ${\displaystyle a_{1},a_{2},...,a_{n}}$ باشد، بنابر الگوریتم تقسیم اعدادی صحیح مانند ${\displaystyle q}$ و ${\displaystyle r}$ وجود دارند که

(۱) ${\displaystyle k=[a_{1},a_{2},...,a_{n}]q+r}$ و ${\displaystyle 0\leq r<[a_{1},a_{2},...,a_{n}]}$

از طرف دیگر ${\displaystyle a_{i}|[a_{1},a_{2},...,a_{n}]}$ و ${\displaystyle a_{i}|k}$ برای هر ${\displaystyle 1\leq i\leq n}$

بنابراین ${\displaystyle a_{i}|r}$

یعنی ${\displaystyle r}$ مضربی مشترک از ${\displaystyle a_{1},a_{2},...,a_{n}}$ است. در نتیجه اگر ${\displaystyle r>0}$، آنگاه ${\displaystyle r\geq [a_{1},a_{2},...,a_{n}]}$، که با نابرابری سمت راست (۱) تناقض دارد بنابراین ${\displaystyle r=0}$ و ${\displaystyle k|[a_{1},a_{2},...,a_{n}]}$

محاسبه ک.م.م.

برای محاسبه ک.م.م. می‌توان همه اعداد را به عوامل اول تجزیه کرد. ک.م.م. برابر حاصل ضرب عوامل مشترک با توان بزرگتر و عوامل غیر مشترک می‌شود. همچنین می‌توان ک.م.م. را به کمک ب.م.م. تعریف نمود: از آنجا که ب م م دو عدد برابر با حاصل ضرب آنها تقسیم بر ک.م.م. آنها است،[5] ک.م.م. دو عدد برابر با حاصل ضرب آنها تقسیم بر ب.م. م آنهاست:

${\displaystyle \operatorname {lcm} (a,b)={\frac {|a\cdot b|}{\gcd(a,b)}}}$

از آنجا که ب.م.م. دو عدد شمارنده هر دو است،[1][6][7] بهتر است اول تقسیم و سپاس ضرب کرد که بدین ترتیب ک.م.م. به این شکل تعریف خواهد شد:

${\displaystyle \operatorname {lcm} (a,b)=\left({|a| \over \gcd(a,b)}\right)\cdot |b|=\left({|b| \over \gcd(a,b)}\right)\cdot |a|.}$

جستارهای وابسته

• بزرگ‌ترین مقسوم‌علیه مشترک

ارجاعات

1. "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-30.
2. Weisstein, Eric W. "Least Common Multiple". mathworld.wolfram.com. Retrieved 2020-08-30.
3. Hardy & Wright, § 5.1, p. 48
4. Long (1972, p. 39)
5. Slavin, Keith R. (2008). "Q-Binomials and the Greatest Common Divisor". INTEGERS: The Electronic Journal of Combinatorial Number Theory. University of West Georgia, Charles University in Prague. 8: A5. Retrieved 2008-05-26.
6. Long (1972, p. 33)
7. Pettofrezzo & Byrkit (1970, p. 34)

منابع

• Crandall, Richard; Pomerance, Carl (2001), Prime Numbers: A Computational Perspective, New York: Springer, ISBN 0-387-94777-9
• Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
• Landau, Edmund (1966), Elementary Number Theory, New York: Chelsea
• Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77-171950
• Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766