اتم هیدروژن

اتم هیدروژن، یک تک اتم عنصر شیمیایی هیدروژن است. اتمی که از نظر الکتریکی خنثی است و دارای یک بار مثبت یا پروتون و یک بار منفی یا الکترون است که با کمک نیروی کولن به هسته پیوند خورده‌است. هیدروژن اتمی سازندهٔ جرم ۷۵٪ عنصرهای جهان است.[1] (بیشتر جرم جهان به صورت عنصرهای شیمیایی نیست-به صورت مادهٔ باریونی است-که از مادهٔ تاریک و انرژی تاریک ساخته شده‌است)

اتم هیدروژن
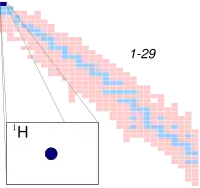{{{image_caption}}} جدول گسترده
کلیات
نام، نماد	protium,¹H
نوترون‌ها	0
پروتون‌ها	1
اطلاعات هسته
فراوانی طبیعی	99.985%
جرم ایزوتوپ	1.007825 u
اسپین	1/2
Excess energy	7288.969± 0.001 keV
انرژی بستگی	0.000± 0.0000 keV

نگاره‌ای از اتم هیدروژن که در آن بزرگی پروتون مرکزی و قطر اتم، هر دو نشان داده شده‌است. قطر اتم تقریباً دو برابر شعاع بدست آمده توسط مدل بور است. (مقیاس این نگاره دقیق نیست)

در زندگی روزانه در زمین اتم هیدروژن یا هیدروژن تک اتمی به سختی پیدا می‌شود ولی برخلاف آن هیدروژن دوست دارد با دیگر عنصرها یا با خودش آمیخته شود و گاز هیدروژن (مولکول دواتمی) را بسازد.

واکنش پذیری و تولید

پیوند H - H یکی از قوی‌ترین پیوندهای شیمیایی است و آنتالپی گسستگی آن در ۲۹۸ کلوین، ۴۳۵٫۸۸ kJ/mol می‌باشد. از آنجایی که پیوند H - H بسیار قوی است، جداسازی هیدروژن بسیار دشوار است مگر در دماهای بالا. برای نمونه در دمای ۳۰۰۰ کلوین درجهٔ جداسازی هیدروژن تنها ۷٫۸۵٪ است.[2]

H_۲

{\overrightarrow {\leftarrow }}

۲ H

ایزوتوپ‌ها

فراوان‌ترین ایزوتوپ این عنصر، هیدروژن-۱ یا پروتیم یا هیدروژن سبک است. این ایزوتوپ هیچ نوترونی ندارد. ( تنها اتم بدون نوترون و پایدار ) دیگر ایزوتوپ‌های هیدروژن مانند دوتریوم، نوترون بیشتری دارد. رابطه‌هایی که در پایین آورده شده‌است برای هر سه ایزوتوپ هیدروژن کار می‌کند. تنها مقدار ثابت ریدبرگ گوناگون است و برای هر ایزوتوپ باید اصلاح شود.

پردازش مکانیک کوانتومی

اتم هیدروژن در مکانیک کوانتوم و نظریهٔ میدان‌های کوانتومی از اهمیت ویژه‌ای برخوردار است.

در ۱۹۱۴ نیلز بور با در نظر گرفتن چند فرض ساده‌کننده توانست بسامدهای طیفی هیدروژن را بدست آورد. فرض‌هایی که بور کرد پایهٔ مدل بور بود. همهٔ این فرض‌ها درست نبود اما در نهایت بور را به مقدار انرژی درستی رساند. در سال‌های ۱۹۲۵ تا ۱۹۲۶ درستی نتایج بور در بسامدها و ترازهای انرژی، توسط مکانیک کوانتوم و با بهره‌گیری از معادلهٔ شرودینگر نشان داده شد. معادلهٔ شرودینگر تراز انرژی هیدروژن و از آن بسامدهای خط‌های طیفی هیدروژن را محاسبه می‌کرد. همچنین با کمک این معادله می‌شد تابع موج الکترون‌ها (ابر الکترونی) را هم برای چندین حالت کوانتومی بدست آورد و در نتیجهٔ آن برای ویژگی ناهمسانگردی پیوندهای اتمی توضیحی پیدا کرد، چیزی که مدل بور در آن ناتوان بود.

معادلهٔ شرودینگر را می‌توان برای اتم‌ها و مولکول‌های پیچیده‌تر هم بکار بُرد.

حل معادلهٔ شرودینگر: بازبینی نتایج

حل معادلهٔ شرودینگر (معادلات موج) برای اتم هیدروژن با بهره‌گیری از این واقعیت است که نیروی کولن پدید آمده توسط هسته، همسانگرد است (از نظر شعاعی در فضا متقارن است و تنها به فاصله از هسته بستگی دارد).

تراز انرژی

تراز انرژی هیدروژن و از جملهٔ آن ریزساختار از رابطهٔ زیر بدست می‌آید:

E_{jn}={\frac {-13.6\ \mathrm {eV} }{n^{2}}}\left[1+{\frac {\alpha ^{2}}{n^{2}}}\left({\frac {n}{j+{\frac {1}{2}}}}-{\frac {3}{4}}\right)\right],

که در آن α ثابت ریزساختار و j عددی است برابر گشتاور زاویه‌ای مقدار ویژه‌است. مقدار 13.6 eV ثابت ریدبرگ نام دارد و از مدل بور می‌توان آن را بدست آورد:

-13.6\ \mathrm {eV} =-{\frac {m_{e}q_{e}^{4}}{8h^{2}\varepsilon _{0}^{2}}},

در این رابطه، m_e جرم الکترون و q_e بار الکترون است. h ثابت پلانک و ε_۰ ثابت گذردهی خلأ است.

ثابت ریدبرگ با کمک معادلهٔ زیر با ثابت ریزساختار رابطه پیدا می‌کند:

-13.6\ \mathrm {eV} =-{\frac {m_{e}c^{2}\alpha ^{2}}{2}}=-{\frac {0.51\mathrm {MeV} }{2\cdot 137^{2}}}.

این ثابت بیشتر در فیزیک اتمی در یکای انرژی ریدبرگ کاربرد دارد:

1\ \mathrm {Ry} \equiv hcR_{\infty }=13.605\;692\;53(30)\ \mathrm {eV} .

[3]

مقدار دقیق ثابت ریدبرگ در بالا با این فرض است که هسته نسبت به الکترون دارای جرم بی‌نهایت است. برای هیدروژن-۱، هیدروژن-۲ (دوتریوم) و هیدروژن-۳ (تریتیوم) این ثابت باید اندکی اصلاح شود تا بتوان ذر سامانه به جای جرم ساده شدهٔ الکترون، جرم کاهش یافته را بکار برد. البته چون هسته بسیار سنگین تر از الکترون است می‌توان گفت مقدار این دو یکسان است. ثابت ریدبرگ R_M برای یک اتم هیدروژن (با یک الکترون) برابر است با: $R_{M}={\frac {R_{\infty }}{1+m_{\mathrm {e} }/M}},$ که در آن $m_{\mathrm {e} }$ جرم الکترون و M جرم هستهٔ اتم است. برای هیدروژن-۱ مقدار $m_{\mathrm {e} /M},$ در حدود ۱/۱۸۳۶ است. این مقدار برای دوتریوم و تریتوم به ترتیب ۱/۳۶۷۰ و ۱/۵۴۹۷ می‌باشد.

تابع موج

در دستگاه مختصات کروی، تابع موج عمود بر سطح شده (نرمال شده) عبارت است از:[4]

\psi _{n\ell m}(r,\vartheta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )\cdot Y_{\ell }^{m}(\vartheta ,\varphi )

نمایش سه بعدی حالت پایهٔ

\psi _{4,3,1}

. در این حالت ۴۵ درصد احتمال دارد که الکترون‌ها پیرامون جسم نشان داده پیدا شوند.

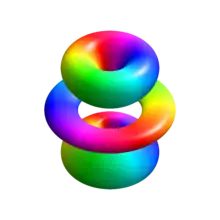
که در آن:

\rho ={2r \over {na_{0}}}

،

a_{0}

شعاع بور است،

L_{n-\ell -1}^{2\ell +1}(\rho )

چندجمله‌ای‌های عمومی لاگر از درجهٔ n − ℓ − ۱ و

Y_{\ell }^{m}(\vartheta ,\varphi )\,

یک تابع هماهنگ کروی از درجهٔ ℓ و ترتیب m است.

گشتاور زاویه‌ای

مقدار ویژه برای عملگر گشتاور زاویه‌ای به قرار زیر است:

L^{2}\,|n,\ell ,m\rangle ={\hbar }^{2}\ell (\ell +1)\,|n,\ell ,m\rangle

L_{z}\,|n,\ell ,m\rangle =\hbar m\,|n,\ell ,m\rangle .

جستارهای وابسته

انیمیشن مدل اتمی بور برای اتم هیدروژن

منابع

Palmer, D. (13 September 1997). "Hydrogen in the Universe". NASA. Retrieved 5 February 2008.
Greenwood, N. N. ; & Earnshaw, A. (1997). Chemistry of the Elements (2nd Edn.), Oxford:Butterworth-Heinemann. ISBN 0-7506-3365-4.
P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants. National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞
David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. pp. ۱۶۲–. ISBN 978-3-527-40601-2. Retrieved 27 June 2011.

پیوند به بیرون

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Palmer, D. (13 September 1997). "Hydrogen in the Universe". NASA. Retrieved 5 February 2008.

[2] Greenwood, N. N. ; & Earnshaw, A. (1997). Chemistry of the Elements (2nd Edn.), Oxford:Butterworth-Heinemann. ISBN 0-7506-3365-4.

[codata-3] P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants. National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞

[4] David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. pp. ۱۶۲–. ISBN 978-3-527-40601-2. Retrieved 27 June 2011.