تئوری تیر تیموشنکو

تئوری تیر تیموشنکو ((به انگلیسی: Timoshenko beam theory)) در اویل قرن بیستم توسط دانشمند و مهندس روس استفن تیموشنکو (به انگلیسی: Stephen Timoshenko) که اصالتی اکراینی داشت ارائه شد.[1][2] این مدل با در نظر گرفتن اثر همزمان تغییرشکل برشی و ممان پیچشی، به مدلی مناسب برای شرح رفتار تیرهای کوتاه، تیرهای مرکب ساندویچی (به انگلیسی: sandwich composite beams) و تیرهای تحت تأثیر تحریک‌کننده فرکانس بالا (در طول موج‌های نزدیک به ضخامت تیر) بدل شد.
فرضیات تئوری تیر تیموشنکو:

1. هر صفحه به صورت صفحه باقی می‌ماند.
2. ضخامت تیر بعد از تغییر شکل تغییر نمی‌کند.

تغییر شکل یک تیر تیموشنکو (آبی) در مقایسه با یک تیر اویلر-برنولی (قرمز).

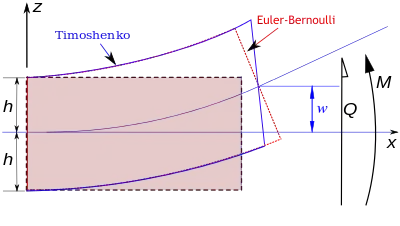
همانطور که در تصویر مشاهده می‌کنید فرض عمود باقی ماندن صفحات عمود بر محور خنثی که در تئوری اویلر-برنولی وجود داشت در اینجا حذف شده‌است. در واقع در تیر تیموشنکو، تغییرشکل‌های برشی خود را به صورت تغییر در زاویه این صفحات نشان می‌دهند.[3][4]

در معادله جواب در این روش علاوه بر وجود یک ترم درجه چهار، یک مشتق جزئی درجه دوم نیز وجود دارد (بر خلاف تئوری تیر اویلر-برنولی).

تیر تیموشنکو تحت بارگذاری استاتیکی

در حالت بارگذاری استاتیکی در تئوری تیر تیموشنکو و بدون در نظر گرفتن نیروهای محوری، فرض می‌شود که تغییر مکان از رابطه زیر بدست می‌آید:

تغییر شکل تیر تیموشنکو. محور عمود بر مقطع تیر به اندازه ${\displaystyle \theta _{x}=\varphi (x)}$ چرخیده است که این مقدار با ${\displaystyle dw/dx}$ برابر نیست .

${\displaystyle u_{x}(x,y,z)=-z~\varphi (x)~;~~u_{y}(x,y,z)=0~;~~u_{z}(x,y)=w(x)}$

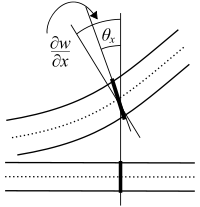
اگر ${\displaystyle (x,y,z)}$ مختصات یک نقطه بر روی تیر باشند ${\displaystyle u_{x},u_{y},u_{z}}$ بردارهای تغییرمکان آن نقطه در راستای دستگاه مختصات فرضی است. ${\displaystyle \varphi }$ زاویه چرخش بردار عمود بر صفحه میانی تیر و ${\displaystyle w}$ تغییرمکان این صفحه در راستای ${\displaystyle z}$ است.

معادلات حاکم بر مسئله که از نوع معادلات دیفرانسیل معمولی هستند از این قرار خواهند بود:

${\displaystyle {\begin{aligned}&{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} \varphi }{\mathrm {d} x}}\right)=q(x,t)\\&{\frac {\mathrm {d} w}{\mathrm {d} x}}=\varphi -{\frac {1}{\kappa AG}}{\frac {\mathrm {d} }{\mathrm {d} x}}\left(EI{\frac {\mathrm {d} \varphi }{\mathrm {d} x}}\right).\end{aligned}}}$

تئوری تیر تیموشنکو در حالت استاتیکی و در صورتی که طرف راست معادله فوق ناچیز در نظر گرفته شود با تئوری اویلر-برنولی برابر خواهد بود. این برابری تنها با وجود شرط زیر برقرار است:

${\displaystyle {\frac {EI}{\kappa L^{2}AG}}\ll 1}$

که در عبارت فوق:

• ${\displaystyle L}$ طول تیر
• ${\displaystyle A}$ سطح مقطع تیر
• ${\displaystyle E}$ مدول الاستیسیته تیر
• ${\displaystyle G}$ مدول برشی تیر
• ${\displaystyle I}$ گشتاور دوم سطح تیر
• و ${\displaystyle \kappa }$ ضریب برش تیموشنکو است که به سطح مقطع تیر بستگی دارد. این عدد برای مقاطع مستطیلی برابر با ${\displaystyle \kappa =5/6}$ است.

با ترکیب دو معادله فوق برای یک تیر همگن با سطح مقطع ثابت خواهیم داشت:

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x)-{\cfrac {EI}{\kappa AG}}~{\cfrac {\mathrm {d} ^{2}q}{\mathrm {d} x^{2}}}}$

لنگر خمشی ${\displaystyle M_{xx}}$ و نیروی برشی ${\displaystyle Q_{x}}$ تیر نیز برای یک تیر الاستیک خطی تیموشنکو با استفاده از معادلات زیر به جابه جایی ${\displaystyle w}$ و چرخش تیر ${\displaystyle \varphi }$ مربوط خواهند شد:

${\displaystyle M_{xx}=-EI~{\frac {\partial \varphi }{\partial x}}\quad {\text{and}}\quad Q_{x}=\kappa ~AG~\left(-\varphi +{\frac {\partial w}{\partial x}}\right)\,.}$

شرایط مرزی

دو معادلهٔ تغییر شکل در تیر تیموشنکو، توسط شرایط مرزی مسئله قابل حل خواهند شد. برای حل دقیق این معادلات به چهار شرط مرزی نیاز است. انواع شرایط مرزی قابل اعمال بر مسئله به صورت زیر خواهد بود:

• تیرهای دارای تکیه گاه مفصلی در دو انتها:

1. تغییر مکان ${\displaystyle w}$ در دو انتهای تیر (در محل تکیه گاه‌ها) برابر صفر است.
2. لنگر خمشی اعمال شده به تیر ${\displaystyle M_{xx}}$ باید معلوم باشد.
3. نیروی برشی ${\displaystyle Q_{x}}$ و میزان چرخش ${\displaystyle \varphi }$ تعیین نشده‌است.

• تیرهای دارای تکیه گاه گیردار :

1. تغییرمکان ${\displaystyle w}$ و زاویه چرخش ${\displaystyle \varphi }$ در محل تکیه گاه صفر است.
2. اگر یک انتهای تیر آزاد باشد (مانند تیر یک سر در گیر یا تیر کنسول) آنگاه نیروی برشی ${\displaystyle Q_{x}}$ و لنگر خمشی ${\displaystyle M_{xx}}$ باید معلوم باشد.

مثال: تیر کنسول

یک تیر کنسول تیموشنکو تحت بار متمرکز در انتهای آزاد تیر.

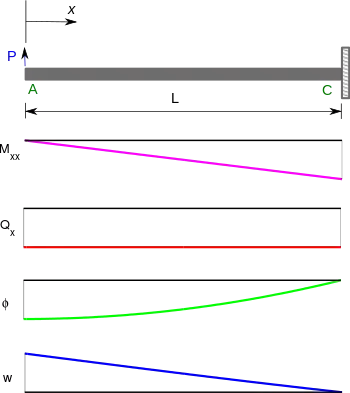
همانطور که می‌دانید در یک تیر کنسول یک سر تیر دارای تکیه گاه گیردار بوده و انتهای دیگر تیر آزاد است. دستگاه مختصات را در سمت چپ تیر و در انتهای آزاد آن مستقر می‌کنیم. در این حالت جهت مثبت ${\displaystyle x}$ به سمت راست و جهت مثبت ${\displaystyle z}$ به سمت بالا اشاره می‌کند. فرض می‌کنیم که نیرو در جهت مثبت محورهای مختصات اعمال شده و گشتاور نیز به صورت ساعت گرد به تیر اعمال می‌گردد. همچنین فرض می‌کنیم که تنش‌های ناشی از ${\displaystyle M_{xx}}$ وقتی تار پایینی تیر تحت فشار باشد و ${\displaystyle Q_{x}}$ وقتی مقطع تیر به صورت پاد ساعت‌گرد تحت پیچش قرار می‌گیرد مثبت است. انتهای گیر دار تیر در ${\displaystyle x=L}$ و انتهای آزاد آن در ${\displaystyle x=0}$ قراردارد. اگر نیروی متمرکز ${\displaystyle P}$ بر انتهای آزاد تیر و در راستای مثبت محور ${\displaystyle z}$ اعمال گردد با رسم نمودار جسم آزاد تیر خواهیم داشت:

${\displaystyle -Px-M_{xx}=0\implies M_{xx}=-Px}$

و

${\displaystyle P+Q_{x}=0\implies Q_{x}=-P\,.}$

در نتیجه با توجه به روابط لنگر خمشی و نیروی برشی داریم:

${\displaystyle Px=EI\,{\frac {d\varphi }{dx}}\qquad {\text{and}}\qquad -P=\kappa AG\left(-\varphi +{\frac {dw}{dx}}\right)\,.}$

با انتگرال گیری از معادله اول و اعمال شرط مرزی ${\displaystyle \varphi =0}$ در ${\displaystyle x=L}$ به عبارت زیر می‌رسیم:

${\displaystyle \varphi (x)=-{\frac {P}{2EI}}\,(L^{2}-x^{2})\,.}$

همچنین معادله دوم را نیز می‌توان به صورت زیر بازنویسی کرد:

${\displaystyle {\frac {dw}{dx}}=-{\frac {P}{\kappa AG}}-{\frac {P}{2EI}}\,(L^{2}-x^{2})\,.}$

که با انتگرال‌گیری و اعمال شرط مرزی ${\displaystyle w=0}$ در ${\displaystyle x=L}$ خواهیم داشت:

${\displaystyle w(x)={\frac {P(L-x)}{\kappa AG}}-{\frac {Px}{2EI}}\,\left(L^{2}-{\frac {x^{2}}{3}}\right)+{\frac {PL^{3}}{3EI}}\,.}$

و در نهایت تنش محوری نیز از رابطه زیر بدست خواهد آمد:

${\displaystyle \sigma _{xx}(x,z)=E\,\varepsilon _{xx}=-E\,z\,{\frac {d\varphi }{dx}}=-{\frac {Pxz}{I}}={\frac {M_{xx}z}{I}}\,.}$

تیر دینامیک تیموشنکو

در تئوری تیر تیموشنکو بدون در نظر گرفتن اثرات محوری، تغییر مکان تیر با توجه به زمان براساس رابطه زیر محاسبه می‌گردد:

${\displaystyle u_{x}(x,y,z,t)=-z~\varphi (x,t)~;~~u_{y}(x,y,z,t)=0~;~~u_{z}(x,y,z,t)=w(x,t)}$

در این رابطه، ${\displaystyle (x,y,z)}$ مختصات یک نقطه بر روی تیر، ${\displaystyle u_{x},u_{y},u_{z}}$ بردارهای جابه جایی این نقطه در راستای محورهای مختصات، ${\displaystyle \varphi }$ زاویه چرخش صفحه عمود بر تار میانی تیر و ${\displaystyle w}$ میزان جابه جایی تار میانی تیر در راستای ${\displaystyle z}$ است. با توجه به فرضیات فوق، امکان توصیف ارتعاش در تئوری تیر تیموشنکو با استفاده از یک جفت معادله دیفرانسیل با مشتقات جزئی وجود خواهد داشت.[5]

${\displaystyle \rho A{\frac {\partial ^{2}w}{\partial t^{2}}}-q(x,t)={\frac {\partial }{\partial x}}\left[\kappa AG\left({\frac {\partial w}{\partial x}}-\varphi \right)\right]}$

${\displaystyle \rho I{\frac {\partial ^{2}\varphi }{\partial t^{2}}}={\frac {\partial }{\partial x}}\left(EI{\frac {\partial \varphi }{\partial x}}\right)+\kappa AG\left({\frac {\partial w}{\partial x}}-\varphi \right)}$

در معادلات فوق متغیرهای وابسته ${\displaystyle w(x,t)}$ بیانگر جابه جایی تیر و ${\displaystyle \varphi (x,t)}$ بیانگر تغییرمکان زاویه‌ای تیر است. باید توجه داشت که بر خلاف تئوری تیر اویلر-برنولی، { نیاز به ترجمه دقیق: the angular deflection is another variable and not approximated by the slope of the deflection.} همچنین سایر متغیرها به صورت زیر تعریف می‌گردند:

• ${\displaystyle \rho }$ چگالی مصالح تیر (توجه شود که منظور چگالی خطی تیر نیست)
• ${\displaystyle A}$مساحت سطح مقطع تیر.
• ${\displaystyle E}$ مدول الاستیسیته.
• ${\displaystyle G}$ مدول برشی.
• ${\displaystyle I}$ گشتاور دوم سطح.
• ${\displaystyle \kappa }$ ضریب برش تیموشنکو است که به سطح مقطع تیر بستگی دارد. این عدد برای مقاطع مستطیلی برابر با ${\displaystyle \kappa =5/6}$
• ${\displaystyle q(x,t)}$ بار توزیع شده (نیرو بر سطح).
• ${\displaystyle m:=\rho A}$
• ${\displaystyle J:=\rho I}$

که البته این مقادیر الزاماً ثابت نیستند. برای یک تیر الاستیک خطی ایزوتروپیک همگن با مقطع ثابت می‌توان با ترکیب دو معادله فوق، معادله زیر را بدست آورد:[6][7]

${\displaystyle EI~{\cfrac {\partial ^{4}w}{\partial x^{4}}}+m~{\cfrac {\partial ^{2}w}{\partial t^{2}}}-\left(J+{\cfrac {EIm}{kAG}}\right){\cfrac {\partial ^{4}w}{\partial x^{2}~\partial t^{2}}}+{\cfrac {mJ}{kAG}}~{\cfrac {\partial ^{4}w}{\partial t^{4}}}=q(x,t)+{\cfrac {J}{kAG}}~{\cfrac {\partial ^{2}q}{\partial t^{2}}}-{\cfrac {EI}{kAG}}~{\cfrac {\partial ^{2}q}{\partial x^{2}}}}$

روش بدست آوردن معادله فوق به زبان اصلی

The equations governing the bending of a homogeneous Timoshenko beam of constant cross-section are ${\displaystyle {\begin{aligned}(1)&&\quad m~{\frac {\partial ^{2}w}{\partial t^{2}}}&=\kappa AG~\left({\frac {\partial ^{2}w}{\partial x^{2}}}-{\frac {\partial \varphi }{\partial x}}\right)+q(x,t)~;~~m:=\rho A\\(2)&&\quad J~{\frac {\partial ^{2}\varphi }{\partial t^{2}}}&=EI~{\frac {\partial ^{2}\varphi }{\partial x^{2}}}+\kappa AG~\left({\frac {\partial w}{\partial x}}-\varphi \right)~;~~J:=\rho I\end{aligned}}}$ From equation (1), assuming appropriate smoothness, we have ${\displaystyle {\begin{aligned}(3)&&\quad {\frac {\partial \varphi }{\partial x}}&=-{\cfrac {m}{\kappa AG}}~{\frac {\partial ^{2}w}{\partial t^{2}}}+{\frac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {q}{\kappa AG}}\\(4)&&\quad {\frac {\partial ^{2}q}{\partial t^{2}}}&=m~{\cfrac {\partial ^{4}w}{\partial t^{4}}}-\kappa AG~\left({\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}-{\cfrac {\partial ^{3}\varphi }{\partial x\partial t^{2}}}\right)\end{aligned}}}$ From (3), assuming appropriate smoothness, ${\displaystyle (5)\qquad {\cfrac {\partial ^{3}\varphi }{\partial x^{3}}}=-{\cfrac {m}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}+{\cfrac {\partial ^{4}w}{\partial x^{4}}}+{\cfrac {1}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial x^{2}}}}$ Differentiating equation (2) gives ${\displaystyle (6)\qquad {\cfrac {\partial ^{3}\varphi }{\partial x\partial t^{2}}}={\cfrac {EI}{J}}~{\cfrac {\partial ^{3}\varphi }{\partial x^{3}}}+{\cfrac {\kappa AG}{J}}~\left({\frac {\partial ^{2}w}{\partial x^{2}}}-{\frac {\partial \varphi }{\partial x}}\right)}$ From equations (4) and (6) ${\displaystyle (7)\qquad {\cfrac {1}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial t^{2}}}-{\cfrac {m}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial t^{4}}}+{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}={\cfrac {EI}{J}}~{\cfrac {\partial ^{3}\varphi }{\partial x^{3}}}+{\cfrac {\kappa AG}{J}}~\left({\frac {\partial ^{2}w}{\partial x^{2}}}-{\frac {\partial \varphi }{\partial x}}\right)}$ From equations (3) and (7) ${\displaystyle (8)\qquad {\cfrac {1}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial t^{2}}}-{\cfrac {m}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial t^{4}}}+{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}={\cfrac {EI}{J}}~{\cfrac {\partial ^{3}\varphi }{\partial x^{3}}}+{\cfrac {m}{J}}~{\frac {\partial ^{2}w}{\partial t^{2}}}-{\cfrac {q}{J}}}$ Plugging equation (5) into (8) gives ${\displaystyle (9)\qquad {\cfrac {J}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial t^{2}}}-{\cfrac {mJ}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial t^{4}}}+J~{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}=-{\cfrac {mEI}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}+EI~{\cfrac {\partial ^{4}w}{\partial x^{4}}}+{\cfrac {EI}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial x^{2}}}+m~{\frac {\partial ^{2}w}{\partial t^{2}}}-q}$ Rearrange to get ${\displaystyle EI~{\cfrac {\partial ^{4}w}{\partial x^{4}}}+m~{\frac {\partial ^{2}w}{\partial t^{2}}}-\left(J+{\cfrac {mEI}{\kappa AG}}\right)~{\cfrac {\partial ^{4}w}{\partial x^{2}\partial t^{2}}}+{\cfrac {mJ}{\kappa AG}}~{\cfrac {\partial ^{4}w}{\partial t^{4}}}=q+{\cfrac {J}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial t^{2}}}-{\cfrac {EI}{\kappa AG}}~{\frac {\partial ^{2}q}{\partial x^{2}}}\quad \square }$

اثرات محوری

برای مشاهدهٔ اثرات محوری در تئوری تیر تیموشنکو به نسخهٔ انگلیسی این مطلب مراجعه فرمایید و در صورت تمایل می‌توانید ترجمه خود از نسخهٔ انگلیسی را نیز در این قسمت اضافه کنید.

میرایی

برای مشاهدهٔ میرایی در تئوری تیر تیموشنکو به نسخهٔ انگلیسی این مطلب مراجعه فرمایید و در صورت تمایل می‌توانید ترجمه خود از نسخهٔ انگلیسی را نیز در این قسمت اضافه کنید.

ضریب برش

برای مشاهدهٔ ضریب در تئوری تیر تیموشنکو به نسخهٔ انگلیسی این مطلب مراجعه فرمایید و در صورت تمایل می‌توانید ترجمه خود از نسخهٔ انگلیسی را نیز در این قسمت اضافه کنید.

منابع

1. Timoshenko, S. P. , 1921, On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 744.
2. Timoshenko, S. P. , 1922, On the transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 125.
3. Bending
4. Kwon. Young W, Bang. Hyochoong, "The Finite Element Method Using MATLAB, Second Edition (Mechanical and Aerospace Engineering Series)", CRCPress, 1996, Pages 244-245.
5. Timoshenko's Beam Equations
6. Thomson, W. T. , 1981, Theory of Vibration with Applications
7. Rosinger, H. E. and Ritchie, I. G. , 1977, On Timoshenko's correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys. , vol. 10, pp. 1461-1466.