خمش

در مهندسی مکانیک، چگونگی رفتار یک عضو سازه بر اثر یک نیروی خارجی وارد شده به صورت عمود بر محور طولی آن توسط خمش توصیف و بیان می‌شود. عضو سازه‌ای به این صورت فرض می‌شود که حداقل یک بعد آن در مقایسه با دو بعد دیگر نسبت ۱/۱۰ یا کمتر را داشته باشد. هنگامی که طول عضوی به‌طور قابل توجه بزرگ تر از عرض و ضخامت باشد، به آن تیر می گویند. یک میله جالباسی را تصور کنید تحت نیروی وزن لباس‌ها خم شده است، این می‌تواند مثالی از یک تیر باشد که تحت خمش قرار گرفته‌است.

خمش یک تیر I شکل

خمش شبه استاتیک در تیرها

هنگامی که یک تیر تحت بار عرضی (نیرو به صورت عمود بر محور طولی آن وارد شود) قرار گیرد، باعث ایجاد تنش و تغییر شکل در آن می‌شود. در وضع شبه ایستایی، مقدار تنش و خیز ایجاد شده در تیر فرض می‌شود که نسبت به زمان ثابت است. همانطور که در تصویر پیداست، یک تیر افقی که از دو طرف توسط تکیه گاه‌هایی مهار شده و در وسط آن نیرویی به سمت پایین وارد شده است، موادی که بر روی تیر قرار دارند دچار فشردگی و موادی که در زیر قرار دارند، دچار کشیدگی می‌شوند.

دو فرم تنش داخلی به هنگام وارد شدن یک بار عرضی شکل می‌گیرد:

تنش برشی که همسو با نیروی وارد شده‌است.
تنش فشاری قائم در ناحیه بالایی و تنش کششی قائم در ناحیه زیرین تیر.

تئوری خمش اویلر-برنولی

عضو یک تیر خم شده: بافت‌ها به صورت هم مرکز، بافت‌های فوقانی تحت فشردگی و بافت‌های تحتانی تحث کشش هستند.

گشتاورهای خمشی در یک تیر

در تئوری اویلر-برنولی برای تیرهای لاغر ، یک فرض مهم این است که مقطع هر صفحه بعد از تغییر شکل صفحه باقی می ماند. به عبارت دیگر از هر گونه تغییر شکل ناشی از تنش برشی در طول مقطع صرف نظر می‌شود. همچنین این توزیع خطی تنها در صورتی قابل اعمال است که تنش ماکزیمم کمتر از تنش تسلیم ماده باشد. برای تنش‌های بزرگتر از تنش تسلیم ، به مقاله ی خمش پلاستیک مراجعه شود. در حالت تسلیم ، بیشترین تنش در مقطع (در دورترین نقاط نسبت به محور خنثی تیر) را قدرت خمشی می نامند. معادله ی اویلر-برنولی برای شرایط شبه استاتیک تیرهای لاغر، همسانگرد و یکنواخت با سطح مقطع ثابت در شرایطی که تحت بار جانبی $q(x)$ قرار گرفته باشند به این صورت است:

$EI~{\cfrac {\mathrm {d} ^{4}w(x)}{\mathrm {d} x^{4}}}=q(x)$

که در آن E مدول یانگ ، I ممان اینرسی مساحت سطح مقطع و $w(x)$ میزان جابجایی محور خنثی تیر است. بعد از دستیابی به جوابی برای میزان خیز تیر ، گشتاور خمشی (M) ، نیروی برشی (Q) درون تیر را می‌توان با روابط زیر محاسبه کرد:

$M(x)=-EI~{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}~;~~Q(x)={\cfrac {\mathrm {d} M}{\mathrm {d} x}}$

خمش ساده ی تیر معمولاً با معادله ی اویلر-برنولی تحلیل می‌شود. شرایط لازم برای استفاده از تئوری خمش ساده به این صورت است:

1. تیر تحت خمش خالص قرار گرفته‌است. به این معنی که نیروی برشی صفر بوده و هیچ گونه بار پیچشی یا نیروی محوری وجود ندارد.
2. ماده همسانگرد و یکنواخت است.
3. ماده از قانون هوک پیروی می‌کند. (به صورت خطی برگشت پذیر بوده و تغییر شکل پلاستیک ندارد.)
4. تیر در ابتدا به صورت مستقیم بوده و در راستای طولی سطح مقطعی ثابت دارد.
5. تیر در صفحه ی خمش یک محور تقارن دارد.
6. بخش‌های تیر به این صورتند که خمش باعث گسیختگی آن می‌شود و نه خرد کردن ، چین دادن یا باکل کردن.
7. سطح مقطع تیر در طول خمش صفحه باقی می ماند.

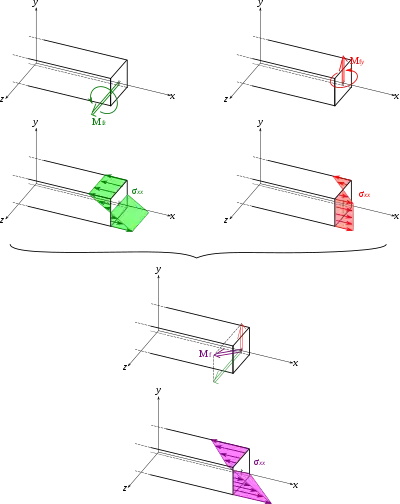
خیز تیری که به صورت متقارن منحرف/جابجا شده و اصل جمع آثار

تحت بار خمشی ، نیروهای فشاری و کششی در جهت محور تیر شکل می‌گیرند. این نیروها تنش‌هایی را ایجاد می‌کنند . ماکزیمم تنش فشاری در بالاترین لبه ی تیر و ماکزیمم تنش کششی در پایین‌ترین لبه ی تیر شکل می‌گیرد. از آنجا که تنش‌های بین این دو کران به صورت خطی تغییر می‌کنند بنابراین نقطه‌ای بر این مسیر خطی وجود دارد که در آن هیچ گونه خمشی وجود ندارد. مکان هندسی این نقاط را محور خنثی گویند. از آنجا که در این ناحیه تنشی وجود ندارد و ناحیه‌های مجاور آن تحت تنش کمی قرار می‌گیرند ، استفاده از تیرهای با مقطع ثابت روش مناسبی برای تحمل بار نیست زیرا در این حالت از کل ظرفیت تیر استفاده نمی‌شود مگر در شرایطی که تیر در حال واژگونی است. تیرهای با فلنج عریض (با مقطع I شکل) و تیر آهن‌ها کاملاً به این ضعف اشاره دارند زیرا استفاده از آن‌ها باعث کمینه شدن مقدار ماده ی استفاده شده در این ناحیه ی با تنش کم می‌شوند.

رابطه ی کلاسیک برای مشخص کردن تنش خمشی در یک تیر تحت بار ساده به این صورت است:

${\sigma }={\frac {My}{I_{x}}}$

که در آن:

${\sigma }$ تنش خمشی
M گشتاور حول محور خنثی
y فاصله ی عمودی تا محور خنثی
I_x ممان اینرسی دوم سطح حول محور خنثی x

تیر تیموشنکو

همانطور که گفته شد از تئوری اولر برنولی برای تیرهای نازک با ضخامت کم استفاده می‌شود . تیموشنکو در سال 1921 روش اولر برنولی را به وسیله ی در نظر گرفتن اثرات تنش برشی بهبود داد که بتوان برای تیرهایی با ضخامت بیشتر و تغییر مکان بیشتر استفاده کرد . فرضیات سینماتیکی تیر تیموشنکو به این صورت می‌باشند :

1- هر صفحه به صورت صفحه باقی می ماند .

2- ضخامت تیر بعد از تغییر شکل تغییر نمی‌کند .

همانطور که دیدید فرض عمود باقی ماندن صفحات عمود بر محور خنثی حذف شده‌است . معادله ی خمش یک تیر خطی الاستیک , ایزوتروپ , همگن با سطح مقطع ثابت در طول با در نظر گرفتن فرضیات بالا به این شکل بیان می‌شود :

(فرمول‌ها از مقاله اصلی در مرجع برداشته شود )

در حالتی که I بیان گر ممان اینرسی سطح , A سطح مقطع , G مدول تنش برشی و K ضریب تصحیح تنش برشی است . برای موادی با ضریب پواسون 0.3 ضریب تصحیح تنش خمشی یک تیر با مقطع مستطیلی به شکل زیر تقریب زده می‌شود :

چرخش خط عمود بر تار خنثی با این معادله حساب می‌شود :

ممان خمشی M و نیروی برشی Q با فرمول‌های زیر محاسبه می‌شوند :

منابع

مشارکت کنندگان ویکی‌پدیای انگلیسیhttp://en.wikipedia.org/w/index.php?title=Bending&oldid=536045945

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.