قانون هوک

قانون هوک در فیزیک، مکانیک و دانش مواد کشسانی (الاستیسیته)، تقریبی است نشان دهندهٔ آن که تغییر طول یک ماده با بار وارد بر آن رابطهٔ خطی دارد. بسیاری از مواد تا زمانی که نیرو از حد کشسانی آن‌ها کمتر باشد با تقریب خوبی از این قانون پیروی می‌کنند. انحراف از قانون هوک با افزایش میزان تغییرشکل زیاد می‌شود به‌طوری‌که در تغییرشکل‌های زیاد، با خارج شدن ماده از دامنه کشسان خطی، این قانون کاربرد خود را از دست می‌دهد. موادی که قانون هوک برای آن‌ها تقریب مناسبی باشد، مواد کشسان خطی یا «مواد هوکی» نام دارند. ساده شدهٔ قانون هوک بیان می‌دارد که کرنش با تنش رابطهٔ مستقیم دارد:

${\displaystyle \mathbf {F} =-k\mathbf {x} \ }$

مکانیک محیط‌های پیوسته
قوانین پایستگی‌ها پایستگی جرم پایستگی تکانه پایستگی انرژی نابرابری‌ها Clausius–Duhem (entropy)
مکانیک جامدات تغییرشکل (مکانیک) کشسانی کشسانی خطی موم‌سانی قانون هوک تنش (مکانیک) کرنش محدود Infinitesimal strain Compatibility خمش Contact mechanics frictional Material failure theory مکانیک شکست
مکانیک سیالات سیال‌ها استاتیک شاره‌ها · دینامیک شاره‌ها اصل ارشمیدس · معادله برنولی معادلات ناویه-استوکس Poiseuille equation · قانون پاسکال گران‌روی (سیال نیوتنی · سیال غیرنیوتنی) شناوری · Mixing · فشار مایع کشش سطحی مویینگی گاز اتمسفر قانون بویل قانون شارل قانون گیلوساک قانون گاز آرمانی پلاسما
رئولوژی ویسکوالاستیسیته رئومتری رئومتر Smart fluid سیال الکترورئولوژیک سیال رئومغناطیسی فروسیال
دانشمندان دانیل برنولی رابرت بویل آگوستین لویی کوشی ژاک شارل لئونارد اویلر ژوزف لویی گیلوساک رابرت هوک بلز پاسکال آیزاک نیوتن کلود-لویی ناویه سر جرج گابریل استوکس، بارونت اول

قانون هوک خواص فیزیکی فنرهای معمولی را برای جابجایی‌های کوچک به خوبی و با دقت بالایی مدل می‌کند. (تصویر متحرک).

که در آن:

x: جابجایی فنر فشرده یا کشیده شده از نقطهٔ تعادل آن. یکای x در دستگاه SI متر است.

F: نیروی بازگردانندهٔ وارده از سوی فنر که با جابجایی انتهای فنر مقاومت می‌کند (نیروی مقاومت فنر)؛ در دستگاه SI یکای آن نیوتن N یا کیلوگرم‌متر بر مجذور ثانیه Kg m s^-۲ است.

k: ثابت فنر است که در دستگاه SI یکای آن نیوتن بر متر یا کیلوگرم بر مجذور ثانیه‌ است.

وقتی چنین رابطه‌ای برای ماده‌ای برقرار باشد، می‌توان گفت که آن ماده رفتار خطی دارد و اگر نتایج آن را بر روی یک نمودار نمایش دهیم می‌بینیم که نتایج به صورت یک خط راست بدست آمده‌اند. علامت منفی در سمت راست رابطهٔ بالا به این دلیل است که نیروی بازگردانندهٔ فنر و جابجایی فنر همواره در جهت مخالف یکدیگر عمل می‌کنند. مثلاً اگر فنر به سمت راست افزایش طول پیدا کند نیروی بازگردانندهٔ آن در سوی مخالف و به سمت چپ یعنی در جهت جمع شدن فنر وارد می‌شود.

قانون هوک پس از قرن ۱۷ میلادی به نام فیزیکدان بریتانیایی رابرت هوک نام‌گذاری شد. وی ابتدا در سال ۱۶۶۰ با عنوان مقلوب لاتین ارائه کرد[3] و در سال ۱۶۷۸ راه حلش را با عنوان رمزی Ut tensio, sic vis به معنی هرچقدرجابجایی همانقدر نیرو، منتشر کرد.

کاربرد عمومی برای مواد کشسانی

قانون هوک می‌تواند پیش‌بینی کند که در اثر یک نیروی مشخص چقدر فنر کشیده خواهد شد.

موادی که پس از وارد شدن یک نیرو و تغییر شکل به سرعت به حالت اولیهٔ خود بازمی‌گردند و مولکول‌ها و اتم‌های آن‌ها نیز به حالت اولیه و تعادل پایدار پیشین خود بازمی‌گردند، معمولاً از قانون هوک پیروی می‌کنند.

یک میله از جنس یک مادهٔ کشسان را می‌توان مانند یک فنر خطی در نظر گرفت، طول میله L و سطح مقطع آن A است. افزایش طول میله (کرنش) آن به صورت خطی با تنش کششی σ وارد بر آن نسبت خطی ثابت دارد. وارون این نسبت خطی را مدول الاستیسیته E می‌نامند؛ بنابراین:

${\displaystyle \sigma =E\varepsilon }$

یا

${\displaystyle \Delta L={\frac {F}{EA}}L={\frac {\sigma }{E}}L.}$

مواد تا زمانی که در بازهٔ کشسانی خود باشند (تنش‌های وارد بر آن‌ها کمتر از تنش تسلیم باشد) از قانون هوک پیروی می‌کنند. در مقابل موادی مانند کائوچو را مواد غیرهوکی می‌نامند در این مواد ویژگی کشسانی ماده به تنش وارد بر آن وابسته‌است و به دمای محیط و نرخ بارگذاری نیز حساس است.

در تغییرشکل‌های کوچک زاویه‌ای، رابطه هوک به صورت زیر بیان می‌شود:

${\displaystyle \tau =G\gamma }$

که در آن، τ تنش برشی اعمال شده بر ماده، γ کرنش زاویه‌ای (برابر تانژانت زاویه پیچش)، و G مدول برشی ماده تحت تنش است. رابطه کرنش زاویه‌ای با زاویه پیچش (θ) به صورت زیر است:[4]

γ = tan(θ) ≈ θ

از قانون هوک در ترازوهای فنری، تحلیل تنش و مدل سازی مواد و … استفاده می‌شود.

معادلهٔ فنر

منحنی تنش-کرنش برای فولاد با کربن کم. قانون هوک تنها میان حالت اولیهٔ فولاد تا زمانی که به نقطهٔ تسلیم برسد بر قرار است. (نقطهٔ شمارهٔ ۲)
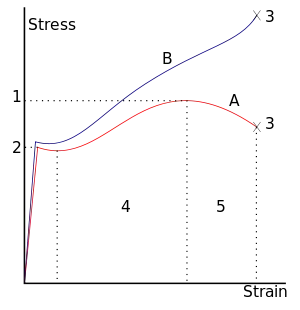
۱. مقاومت نهایی
۲. مقاومت قبل از تسلیم، مطابق نقطهٔ جاری شدن فولاد
۳. شکست
۴. ناحیهٔ سخت شدگی
۵. ناحیهٔ باریک شدگی
A: (F/A_۰)
B: تنش واقعی (F/A)

می‌توان از معادلهٔ فنر به عنوان پر کاربردترین بیان قانون هوک یاد کرد. قانون هوک برای فنر بیان می‌دارد که نسبت نیروی بازگردانندهٔ وارده از سوی فنر به میزان تغییر شکل فنر برابر است با مقدار ثابتی معروف به ثابت فنر یا k با یکای نیرو بر طول:

${\displaystyle F=-kx\,}$

علامت منفی در رابطهٔ بالا به این دلیل است که بردارهای نیرو و جابجایی در خلاف جهت یکدیگر بر این سامانه اثر می‌کنند. نیروی بازگردانندهٔ فنر در برابر هر نوع تغییر شکل مقاومت می‌کند و تلاش می‌کند تا فنر را دوباره به حالت تعادل پیشین خود بازگرداند. کارمایه یا انرژی پتانسیل ذخیره شده در فنر برابر است با:

${\displaystyle PE={1 \over 2}kx^{2}}$

که برابر است با انرژی لازم برای اینکه کم‌کم فنر جمع شود یا انتگرال نیرو روی جابجایی. یادآوری می‌شود که مقدار انرژی پتانسیل فنر همواره بزرگتر از صفر است.

انرژی ذخیره شده را می‌توان به صورت یک نمودار سهمی روی محور U-x نمایش داد. وقتی که فنر در جهت محور x کشیده یا فشرده می‌شود (در هر دو حالت) انرژی پتانسیل آن افزایش می‌ یابد. فنر همواره تلاش می‌کند تا با بازگرداندن خود به حالت تعادل انرژی پتانسیلش را آزاد کند (از دست بدهد) درست مانند توپی که از یک بلندی رها می‌شود و انرژی پتانسیل گرانشی خود را از دست می‌دهد (می‌کاهد).

اگر جرم m به انتهای یک فنر بسته شود و پس از کشیده شدن رها گردد، در حالت آرمانی که اصطکاک نداشته باشیم و جرم فنر نسبت به جرم m ناچیز باشد، فنر و جرم همواره نوسان خواهند کرد که سرعت زاویه‌ای آن برابر خواهد بود با:

${\displaystyle \omega ={\sqrt {k \over m}}}$

بسامد آن برابر است با:

${\displaystyle f={1 \over 2\pi }{\sqrt {k \over m}}.}$

تذکر: رابطه‌های بالا با این فرض گفته شد که فنر بیش از بازهٔ کشسان خود کشیده نشده‌باشد که در غیر این صورت فنر دچار تغییر شکل همیشگی (بدون بازگشت) می‌شود.

سامانه‌ای با چندین فنر

دو فنر را می‌توان به شکل سری یا مواری به یک جرم وصل کرد، که در زیر این دو حالت با یکدیگر مقایسه شده‌اند.

مقایسه	فنرهای موازی	فنرهای سری
ثابت فنر هم‌ارز	${\displaystyle k_{eq}=k_{1}+k_{2}\,}$	${\displaystyle {\frac {1}{k_{eq}}}={\frac {1}{k_{1}}}+{\frac {1}{k_{2}}}\,}$
طول فشردگی	${\displaystyle x_{1}=x_{2}\,}$	${\displaystyle {\frac {x_{1}}{x_{2}}}={\frac {k_{2}}{k_{1}}}\,}$
انرژی ذخیره شده	${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {k_{1}}{k_{2}}}\,}$	${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {k_{2}}{k_{1}}}\,}$

اثبات

ثابت فنر هم‌ارز (سری)

برای بدست آوردن ثابت فنر هم-ارز دو فنر سری ${\displaystyle k_{eq}}$، باید از روش هوشمندانه تری نسبت به حالت دو فنر موازی استفاده کرد. اگر فرض کنیم میزان تغییر شکل در فنر هم‌ارز (که برابر است با موقعیت مکانی جرم انتهای فنرها) برابر با x۲ باشد، برای بدست آوردن ${\displaystyle k_{eq}}$ نیاز داریم تا به رابطه‌ای مانند معادلهٔ زیر برسیم: ${\displaystyle F_{b}=-k_{eq}x_{2}.\,}$ همچنین فرض می‌کنیم که نقطهٔ پیوند میان دو فنر موقعیت x۲ را داشته باشد؛ بنابراین نیروی وارده بر جرم انتهایی برابر است با: ${\displaystyle F_{b}=-k_{2}\left(x_{2}-x_{1}\right).\quad \quad \quad (1)\,}$ همچنین نیروی وارده بر محل پیوند میان دو فنر برابر خواهد بود با: ${\displaystyle F_{s}=-k_{1}x_{1}+k_{2}(x_{2}-x_{1}).\,}$ وقتی که جرم هول داده می‌شود، فنرها فشرده می‌شوند، حال اگر جرم را رها کنیم کل سامانه اجازه پیدا می‌کند تا به حالت تعادل بازگردد وقتی سامانه به سمت تعادل یا نیروی صفر بازمی‌گردد به این معنی است که مجموع نیروهای فنرها برابر با صفر می‌شود. پس ${\displaystyle F_{s}=0}$ می‌شود، برای بدست آوردن ${\displaystyle x_{1}\,}$ می‌نویسیم: ${\displaystyle -k_{1}x_{1}+k_{2}(x_{2}-x_{1})=0\,}$ ${\displaystyle -k_{1}x_{1}-k_{2}x_{1}=-k_{2}x_{2}\,}$ ${\displaystyle \left(k_{1}+k_{2}\right)x_{1}=k_{2}x_{2}\,}$ پس: ${\displaystyle x_{1}={\frac {k_{2}}{k_{1}+k_{2}}}x_{2}.\,}$ مقدار بدست آمدهٔ ${\displaystyle x_{1}\,}$ را در رابطهٔ (۱) جایگزین می‌کنیم: ${\displaystyle F_{b}\,}$ ${\displaystyle =-k_{2}x_{2}+k_{2}x_{1}\,}$ ${\displaystyle =-k_{2}x_{2}+k_{2}\left({\frac {k_{2}}{k_{1}+k_{2}}}x_{2}\right)\,}$ ${\displaystyle =-k_{2}x_{2}\left({\frac {k_{1}+k_{2}}{k_{1}+k_{2}}}\right)+{\frac {k_{2}^{2}}{k_{1}+k_{2}}}x_{2}\,}$ ${\displaystyle =x_{2}{\frac {-k_{1}k_{2}-k_{2}^{2}+k_{2}^{2}}{k_{1}+k_{2}}}\,}$ به این ترتیب نیروی وارده به جرم بدست می‌آید: ${\displaystyle F_{b}=-\left({\frac {k_{1}k_{2}}{k_{1}+k_{2}}}\right)x_{2}.\,}$ می‌توان گفت که عبارت داخل پرانتز ثابت فنر هم‌ارز این سامانه‌است: ${\displaystyle k_{eq}={\frac {k_{1}k_{2}}{k_{1}+k_{2}}}.\,}$ عبارت بالا را بازنویسی می‌کنیم: ${\displaystyle {\frac {1}{k_{eq}}}={\frac {1}{k_{1}}}+{\frac {1}{k_{2}}}.\,}$

ثابت فنر هم‌ارز (موازی)

هر دوی فنرها به جرم موجود در سامانه بسته شده‌اند پس میزان تغییر شکل هر دو فنر با هم برابر است. نیروی وارده به جرم برابر خواهد بود با: ${\displaystyle F_{b}\,}$ ${\displaystyle =F_{1}+F_{2}\,}$ ${\displaystyle =-k_{1}x-k_{2}x\,}$ پس از فاکتورگیری خواهیم داشت: ${\displaystyle F_{b}=-(k_{1}+k_{2})x.\,}$ می‌توان نتیجه گرفت که عبارت داخل پرانتز همان ثابت فنر هم‌ارز این سامانه‌است: ${\displaystyle k_{eq}=k_{1}+k_{2}.\,}$

طول فشردگی

وقتی که دو فنر به صورت سری بسته شده باشند، اندازهٔ نیروی هر دو فنر با هم برابر است: ${\displaystyle |F_{1}|=|F_{2}|\,}$ ${\displaystyle k_{1}x_{1}=k_{2}\left(x_{2}-x_{1}\right).\,}$ x1 میزان تغییر طول فنر یک، و x2 - x1 میزان تغییر طول فنر دو است. تعریف می‌کنیم: ${\displaystyle a_{1}=x_{1}\,}$ ${\displaystyle a_{2}=x_{2}-x_{1}.\,}$ عبارت‌های بالا را جایگزین می‌کنید: ${\displaystyle {\frac {a_{1}}{a_{2}}}={\frac {k_{2}}{k_{1}}}.\,}$

انرژی ذخیره شده

نسبت انرژی ذخیره شده در دو فنر سری عبارت است از: ${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {{\frac {1}{2}}k_{1}a_{1}^{2}}{{\frac {1}{2}}k_{2}a_{2}^{2}}},\,}$ پیش تر رابطهٔ میان a1 و a2 را بدست آورده بودیم که در رابطهٔ بالا جایگزین می‌کنیم: ${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {k_{1}}{k_{2}}}\left({\frac {k_{2}}{k_{1}}}\right)^{2}={\frac {k_{2}}{k_{1}}}.\,}$ برای فنرهای موازی: ${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {{\frac {1}{2}}k_{1}x^{2}}{{\frac {1}{2}}k_{2}x^{2}}}\,}$ چون در فنرهای موازی، میزان فشردگی هر دو فنر با هم برابر است، x از دو طرف تساوی ساده می‌شود: ${\displaystyle {\frac {E_{1}}{E_{2}}}={\frac {k_{1}}{k_{2}}}.\,}$

بیان تنسوری قانون هوک

تذکر: در ادامه از قرارداد جمع‌زنی اینشتین، استفاده شده‌است.

وقتی که با تنش‌های سه بعدی کار می‌کنیم، از تنسور چهارتایی ${\displaystyle {\mathsf {c}}}$ به شکل ${\displaystyle c_{ijk\ell }}$ که دارای ۸۱ ضریب الاستیسیته‌است باید استفاده کرد تا بتوان میان تنسور تنش ${\displaystyle {\boldsymbol {\sigma }}}$ یا (σ_ij) و تنسور کرنش ${\displaystyle {\boldsymbol {\epsilon }}}$ یا (${\displaystyle \epsilon _{k\ell }}$) ارتباط برقرار کرد.

${\displaystyle {\boldsymbol {\sigma }}={\mathsf {c}}:{\boldsymbol {\epsilon }}~.}$

اگر عبارت بالا را به همراه جزئیاتش بنویسیم به شکل زیر خواهد بود (با استفاده از قرارداد جمع‌زنی اینشتین):

${\displaystyle \sigma _{ij}=c_{ijk\ell }~\epsilon _{k\ell }}$

تنسور ${\displaystyle {\mathsf {c}}}$ را تنسور سختی یا تنسور الاستیسیته می‌نامند. به دلیل تقارن تنسورهای تنش و کرنش، در تنسور سختی تنها ۲۱ ضریب از یکدیگر مستقل‌اند. از آنجایی که یکای تنش همان یکای فشار است و کرنش، یکایی ندارد، پس یکای تمامی درایه‌های تنسور سختی ${\displaystyle c_{ijk\ell }}$، همان یکای تنش خواهد بود.

عبارت عمومی قانون هوک را می‌توان شبیه رابطهٔ میان تنش و کرنش نوشت:

${\displaystyle {\boldsymbol {\epsilon }}={\mathsf {s}}:{\boldsymbol {\sigma }}\qquad {\rm {or}}\qquad \epsilon _{ij}=s_{ijk\ell }~\sigma _{k\ell }~.}$

تنسور ${\displaystyle {\mathsf {s}}}$ را تنسور انطباق می‌نامند.

مواد همسان

تذکر: برای آگاهی بیشتر دربارهٔ سیالات، مقالهٔ گرانروی را نگاه کنید.

ویژگی مواد همسان این است که آن‌ها در جهت‌های مختلف ویژگی‌های یکسان از خود نشان می‌دهند؛ بنابراین معادلات فیزیکی که برای مواد همسان نوشته می‌شود باید مستقل از دستگاه مختصات باشد. تنسور کرنش یک تنسور متقارن است. می‌توان تنسور کرنش را بوسیلهٔ اثر آن و دلتای کرونکر ${\displaystyle \delta _{ij}}$ به شکل زیر نمایش داد:[5]^{:Ch. 10}

${\displaystyle \varepsilon _{ij}=\left({\tfrac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)+\left(\varepsilon _{ij}-{\tfrac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)}$

با استفاده از جبر تنسورها خواهیم داشت:

${\displaystyle {\boldsymbol {\varepsilon }}=\mathrm {vol} ({\boldsymbol {\varepsilon }})+\mathrm {dev} ({\boldsymbol {\varepsilon }})~;~~\mathrm {vol} ({\boldsymbol {\varepsilon }}):={\tfrac {1}{3}}~\mathrm {tr} ({\boldsymbol {\varepsilon }})~\mathbf {I} ~;~~\mathrm {dev} ({\boldsymbol {\varepsilon }}):={\boldsymbol {\varepsilon }}-\mathrm {vol} ({\boldsymbol {\varepsilon }})}$

که ${\displaystyle \mathbf {I} }$ تنسور یکهٔ درجه دو است. در سمت راست تساوی، عبارت ${\displaystyle Vol}$ (به انگلیسی: volumetric strain tensor) به معنی تنسور کرنش حجمی است و عبارت ${\displaystyle dev}$ به معنی تنسور اعوجاج یا تنسور کرنش برشی یا تنسور انحرافی (به انگلیسی: deviatoric strain tensor) است.

عمومی‌ترین شکل قانون هوک برای مواد همسان به صورت ترکیب خطی این تنسورها نوشته می‌شود:

${\displaystyle \sigma _{ij}=3K\left({\tfrac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)+2G\left(\varepsilon _{ij}-{\tfrac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)\,~;~~{\boldsymbol {\sigma }}=3K~\mathrm {vol} ({\boldsymbol {\varepsilon }})+2G~\mathrm {dev} ({\boldsymbol {\varepsilon }})}$

در عبارت بالا، K مدول حجمی، و G مدول برشی است.

با استفاده از مدول الاستیک، می‌توان رابطهٔ بالا را بیشتر گسترش داد، در نتیجه دیگر نوشتار تنسوری قانون هوک عبارت است از:[6]

${\displaystyle {\boldsymbol {\sigma }}=\lambda ~\mathrm {tr} ({\boldsymbol {\varepsilon }})~\mathbf {I} +2\mu ~{\boldsymbol {\varepsilon }}={\mathsf {c}}:{\boldsymbol {\varepsilon }}~;~~{\mathsf {c}}=\lambda ~\mathbf {I} \otimes \mathbf {I} +2\mu ~{\mathsf {I}}}$

که در آن ${\displaystyle \lambda$ :=K-2/3G} و ${\displaystyle \mu$ :=G} ثابت‌های لامه اند، ${\displaystyle \mathbf {I} }$ تنسور یکه و ${\displaystyle {\mathsf {I}}}$ تنسور یکهٔ درجهٔ چهار است. با توجه به دستگاه مختصات کارتزین:

${\displaystyle \sigma _{ij}=\lambda ~\varepsilon _{kk}~\delta _{ij}+2\mu ~\varepsilon _{ij}=c_{ijk\ell }~\varepsilon _{k\ell }~;~~c_{ijk\ell }=\lambda ~\delta _{ij}~\delta _{k\ell }+\mu ~(\delta _{ik}~\delta _{j\ell }+\delta _{i\ell }~\delta _{jk})}$

رابطهٔ معکوس عبارت است از:[7]

${\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{2\mu }}~{\boldsymbol {\sigma }}-{\tfrac {\lambda }{2\mu (3\lambda +2\mu )}}~\mathrm {tr} ({\boldsymbol {\sigma }})~\mathbf {I} ={\tfrac {1}{2G}}~{\boldsymbol {\sigma }}+\left({\tfrac {1}{9K}}-{\tfrac {1}{6G}}\right)~\mathrm {tr} ({\boldsymbol {\sigma }})~\mathbf {I} }$

بنابراین تنسور انطباق در رابطهٔ ${\displaystyle {\boldsymbol {\varepsilon }}={\mathsf {s}}:{\boldsymbol {\sigma }}}$، عبارت خواهد بود از:

${\displaystyle {\mathsf {s}}=-{\tfrac {\lambda }{2\mu (3\lambda +2\mu )}}~\mathbf {I} \otimes \mathbf {I} +{\tfrac {1}{2\mu }}~{\mathsf {I}}=\left({\tfrac {1}{9K}}-{\tfrac {1}{6G}}\right)~\mathbf {I} \otimes \mathbf {I} +{\tfrac {1}{2G}}~{\mathsf {I}}}$

با استفاده از مدول یانگ و ضریب پواسون، قانون هوک برای مواد همسان را چنین می‌توان نوشت:

${\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{E}}~{\boldsymbol {\sigma }}-{\tfrac {\nu }{E}}\left[\mathrm {tr} ({\boldsymbol {\sigma }})~\mathbf {I} -{\boldsymbol {\sigma }}\right]}$

در نتیجه کرنش در جهت‌های مختلف را می‌توان به شکل زیر نوشت:

${\displaystyle {\begin{aligned}\varepsilon _{11}&={\tfrac {1}{E}}\left[\sigma _{11}-\nu (\sigma _{22}+\sigma _{33})\right]\\\varepsilon _{22}&={\tfrac {1}{E}}\left[\sigma _{22}-\nu (\sigma _{11}+\sigma _{33})\right]\\\varepsilon _{33}&={\tfrac {1}{E}}\left[\sigma _{33}-\nu (\sigma _{11}+\sigma _{22})\right]\\\varepsilon _{12}&={\tfrac {1}{2G}}~\sigma _{12}~;~~\varepsilon _{13}={\tfrac {1}{2G}}~\sigma _{13}~;~~\varepsilon _{23}={\tfrac {1}{2G}}~\sigma _{23}\end{aligned}}}$

که در آن E مدول الاستیسیته و ${\displaystyle \nu }$ ضریب پواسون است.

قانون هوک در سه بعد

قانون هوک در سه بعد را می‌توان با استفاده از ضریب پواسون و شکل یک بعدی این قانون بدست آورد. فرض کنید در اثر نیروی وارده در جهت (۱) کشش داریم و در جهت‌های (۲ و ۳) عمود بر جهت (۱) جمع شدگی داریم: ${\displaystyle \varepsilon _{1}'={\frac {1}{E}}\sigma _{1}}$, ${\displaystyle \varepsilon _{2}'=-{\frac {\nu }{E}}\sigma _{1}}$, ${\displaystyle \varepsilon _{3}'=-{\frac {\nu }{E}}\sigma _{1}}$, که در آن ${\displaystyle \nu }$ ضریب پواسون و ${\displaystyle E}$ مدول یانگ است. معادلهٔ مشابه را در جهت‌های ۲ و ۳ چنین خواهیم داشت: ${\displaystyle \varepsilon _{1}''=-{\frac {\nu }{E}}\sigma _{2}}$, ${\displaystyle \varepsilon _{2}''={\frac {1}{E}}\sigma _{2}}$, ${\displaystyle \varepsilon _{3}''=-{\frac {\nu }{E}}\sigma _{2}}$, و ${\displaystyle \varepsilon _{1}'''=-{\frac {\nu }{E}}\sigma _{3}}$, ${\displaystyle \varepsilon _{2}'''=-{\frac {\nu }{E}}\sigma _{3}}$, ${\displaystyle \varepsilon _{3}'''={\frac {1}{E}}\sigma _{3}}$. با جمع کردن هر سه حالت ${\displaystyle \varepsilon _{i}=\varepsilon _{i}'+\varepsilon _{i}''+\varepsilon _{i}'''}$ با یکدیگر خواهیم داشت: ${\displaystyle \varepsilon _{1}={\frac {1}{E}}(\sigma _{1}-\nu (\sigma _{2}+\sigma _{3}))}$ ${\displaystyle \varepsilon _{2}={\frac {1}{E}}(\sigma _{2}-\nu (\sigma _{1}+\sigma _{3}))}$ ${\displaystyle \varepsilon _{3}={\frac {1}{E}}(\sigma _{3}-\nu (\sigma _{1}+\sigma _{2}))}$ پس از فاکتورگیری از ${\displaystyle \nu \sigma }$ خواهیم داشت: ${\displaystyle \varepsilon _{1}={\frac {1}{E}}((1+\nu )\sigma _{1}-\nu (\sigma _{1}+\sigma _{2}+\sigma _{3}))}$ ${\displaystyle \varepsilon _{2}={\frac {1}{E}}((1+\nu )\sigma _{2}-\nu (\sigma _{1}+\sigma _{2}+\sigma _{3}))}$ ${\displaystyle \varepsilon _{3}={\frac {1}{E}}((1+\nu )\sigma _{3}-\nu (\sigma _{1}+\sigma _{2}+\sigma _{3}))}$ ${\displaystyle \sigma _{1}}$ از رابطه‌های بالا چنین بدست می‌آید: ${\displaystyle \sigma _{1}={\frac {E}{1+\nu }}\varepsilon _{1}+{\frac {\nu }{1+\nu }}(\sigma _{1}+\sigma _{2}+\sigma _{3})}$. محاسبهٔ مجموع رابطه: ${\displaystyle \sum _{i=1,2,3}\varepsilon _{i}={\frac {1}{E}}((1+\nu )\sum _{i=1,2,3}\sigma _{i}-3\nu (\sum _{i=1,2,3}\sigma _{i}))={\frac {1-2\nu }{E}}\sum _{i=1,2,3}\sigma _{i}}$ ${\displaystyle \sigma _{1}+\sigma _{2}+\sigma _{3}={\frac {E}{1-2\nu }}(\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3})}$ پس از خلاصه کردن ${\displaystyle \sigma _{1}}$ به صورت زیر بدست می‌آید: ${\displaystyle \sigma _{1}={\frac {E}{1+\nu }}\varepsilon _{1}+{\frac {E\nu }{(1+\nu )(1-2\nu )}}(\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3})}$, ${\displaystyle \sigma _{1}=2\mu \varepsilon _{1}+\lambda (\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3})}$, که در روابط بالا، ${\displaystyle \mu }$ و ${\displaystyle \lambda }$ ثابت‌های لامه‌اند. به طریق مشابه اگر معادلات برای جهت‌های (۲ و ۳) نوشته شود، قانون هوک در سه بعد بدست می‌آید.

قانون هوک در قالب ماتریسی برای مواد همسان عبارت است از:

${\displaystyle {\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{31}\\2\varepsilon _{12}\end{bmatrix}}={\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\\gamma _{23}\\\gamma _{31}\\\gamma _{12}\end{bmatrix}}={\cfrac {1}{E}}{\begin{bmatrix}1&-\nu &-\nu &0&0&0\\-\nu &1&-\nu &0&0&0\\-\nu &-\nu &1&0&0&0\\0&0&0&2(1+\nu )&0&0\\0&0&0&0&2(1+\nu )&0\\0&0&0&0&0&2(1+\nu )\end{bmatrix}}{\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{31}\\\sigma _{12}\end{bmatrix}}}$

که در آن ${\displaystyle \gamma _{ij}:=2\varepsilon _{ij}}$ کرنش برشی است. معکوس رابطه چنین است:

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{31}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{(1+\nu )(1-2\nu )}}{\begin{bmatrix}1-\nu &\nu &\nu &0&0&0\\\nu &1-\nu &\nu &0&0&0\\\nu &\nu &1-\nu &0&0&0\\0&0&0&(1-2\nu )/2&0&0\\0&0&0&0&(1-2\nu )/2&0\\0&0&0&0&0&(1-2\nu )/2\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{31}\\2\varepsilon _{12}\end{bmatrix}}}$

با استفاده از ثابت‌های لامه، رابطهٔ بالا را ساده می‌کنیم:

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{31}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}2\mu +\lambda &\lambda &\lambda &0&0&0\\\lambda &2\mu +\lambda &\lambda &0&0&0\\\lambda &\lambda &2\mu +\lambda &0&0&0\\0&0&0&\mu &0&0\\0&0&0&0&\mu &0\\0&0&0&0&0&\mu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{31}\\2\varepsilon _{12}\end{bmatrix}}}$

تنش‌های صفحه‌ای در قانون هوک

در اثر تنش‌های صفحه‌ای، تنش در بعد سوم به شکل ${\displaystyle \sigma _{33}=\sigma _{31}=\sigma _{13}=\sigma _{32}=\sigma _{23}=0}$ خواهد بود؛ در این صورت قانون هوک به شکل زیر ارائه می‌شود:

${\displaystyle {\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\2\varepsilon _{12}\end{bmatrix}}={\cfrac {1}{E}}{\begin{bmatrix}1&-\nu &0\\-\nu &1&0\\0&0&2(1+\nu )\end{bmatrix}}{\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}}$

وارون رابطه به صورت زیر خواهد بود:

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&{\cfrac {1-\nu }{2}}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\2\varepsilon _{12}\end{bmatrix}}}$

مواد ناهمسان

تقارن تنسور تنش کوشی (${\displaystyle \sigma _{ij}=\sigma _{ji}\,}$) و قانون هوک در حالت کلی (${\displaystyle \sigma _{ij}=c_{ijk\ell }~\epsilon _{k\ell }}$) می‌رساند که ${\displaystyle c_{ijk\ell }=c_{jik\ell }\,}$ خواهد بود. به روش مشابه، از تقارن تنسور کرنش‌های بسیار کوچک می‌توان نتیجه گرفت که ${\displaystyle c_{ijk\ell }=c_{ij\ell k}\,}$. این تقارن‌ها را تقارن خردِ[8] تنسور سختی می‌نامند (${\displaystyle {\mathsf {c}}}$).

آنگاه که گرادیان تغییرشکل‌ها و تنش کوشی با هم کار کنند، رابطهٔ تنش - کرنش را می‌توان از تابع چگالی انرژی تغییر شکل‌ها (${\displaystyle {\mathsf {U}}}$) بدست آورد:

${\displaystyle \sigma _{ij}={\cfrac {\partial U}{\partial \epsilon _{ij}}}\quad \implies \quad c_{ijk\ell }={\cfrac {\partial ^{2}U}{\partial \epsilon _{ij}\partial \epsilon _{k\ell }}}~.}$

از دلخواه بودن ترتیب دیفرانسیل‌ها می‌توان نتیجه گرفت که ${\displaystyle c_{ijk\ell }=c_{k\ell ij}\,}$ که این را تقارن بزرگ[9] تنسور سختی می‌نامند. تقارن خُرد و تقارن بزرگ تنسور سختی نتیجه می‌دهد که تنسور سختی تنها ۲۱ درایهٔ مستقل (جزء سازندهٔ مستقل) دارد.

نمایش ماتریسی (تنسور سختی)

معمول است که قانون هوک برای مواد نامسان را به صورت ماتریسی نیز توضیح دهند که آن را مفهوم وویت نیز می‌نامند. برای این کار باید از تقارن تنسورهای تنش و کرنش استفاده کرد و آن‌ها را به صورت یک بردار شش بُعدی در یک دستگاه مختصات متعامد[10] (${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}}$) به صورت زیر توضیح داد:

${\displaystyle [{\boldsymbol {\sigma }}]={\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{31}\\\sigma _{12}\end{bmatrix}}\equiv {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}~;~~[{\boldsymbol {\epsilon }}]={\begin{bmatrix}\epsilon _{11}\\\epsilon _{22}\\\epsilon _{33}\\2\epsilon _{23}\\2\epsilon _{31}\\2\epsilon _{12}\end{bmatrix}}\equiv {\begin{bmatrix}\epsilon _{1}\\\epsilon _{2}\\\epsilon _{3}\\\epsilon _{4}\\\epsilon _{5}\\\epsilon _{6}\end{bmatrix}}}$

آنگاه تنسور سختی (${\displaystyle {\mathsf {c}}}$) را می‌توان چنین نوشت:

${\displaystyle [{\mathsf {C}}]={\begin{bmatrix}c_{1111}&c_{1122}&c_{1133}&c_{1123}&c_{1131}&c_{1112}\\c_{2211}&c_{2222}&c_{2233}&c_{2223}&c_{2231}&c_{2212}\\c_{3311}&c_{3322}&c_{3333}&c_{3323}&c_{3331}&c_{3312}\\c_{2311}&c_{2322}&c_{2333}&c_{2323}&c_{2331}&c_{2312}\\c_{3111}&c_{3122}&c_{3133}&c_{3123}&c_{3131}&c_{3112}\\c_{1211}&c_{1222}&c_{1233}&c_{1223}&c_{1231}&c_{1212}\end{bmatrix}}\equiv {\begin{bmatrix}C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16}\\C_{12}&C_{22}&C_{23}&C_{24}&C_{25}&C_{26}\\C_{13}&C_{23}&C_{33}&C_{34}&C_{35}&C_{36}\\C_{14}&C_{24}&C_{34}&C_{44}&C_{45}&C_{46}\\C_{15}&C_{25}&C_{35}&C_{45}&C_{55}&C_{56}\\C_{16}&C_{26}&C_{36}&C_{46}&C_{56}&C_{66}\end{bmatrix}}}$

قانون هوک به گونهٔ زیر نوشته می‌شود:

${\displaystyle [{\boldsymbol {\sigma }}]=[{\mathsf {C}}][{\boldsymbol {\epsilon }}]\qquad {\text{or}}\qquad \sigma _{i}=C_{ij}\epsilon _{j}~.}$

به روش مشابه تنسور (${\displaystyle {\mathsf {s}}}$) انطباق را چنین می‌توان نوشت:

${\displaystyle [{\mathsf {S}}]={\begin{bmatrix}s_{1111}&s_{1122}&s_{1133}&2s_{1123}&2s_{1131}&2s_{1112}\\s_{2211}&s_{2222}&s_{2233}&2s_{2223}&2s_{2231}&2s_{2212}\\s_{3311}&s_{3322}&s_{3333}&2s_{3323}&2s_{3331}&2s_{3312}\\2s_{2311}&2s_{2322}&2s_{2333}&4s_{2323}&4s_{2331}&4s_{2312}\\2s_{3111}&2s_{3122}&2s_{3133}&4s_{3123}&4s_{3131}&4s_{3112}\\2s_{1211}&2s_{1222}&2s_{1233}&4s_{1223}&4s_{1231}&4s_{1212}\end{bmatrix}}\equiv {\begin{bmatrix}S_{11}&S_{12}&S_{13}&S_{14}&S_{15}&S_{16}\\S_{12}&S_{22}&S_{23}&S_{24}&S_{25}&S_{26}\\S_{13}&S_{23}&S_{33}&S_{34}&S_{35}&S_{36}\\S_{14}&S_{24}&S_{34}&S_{44}&S_{45}&S_{46}\\S_{15}&S_{25}&S_{35}&S_{45}&S_{55}&S_{56}\\S_{16}&S_{26}&S_{36}&S_{46}&S_{56}&S_{66}\end{bmatrix}}}$

تغییر دستگاه مختصات

اگر یک مادهٔ کشسان خطی (الاستکیک خطی) را از حالت مرجع به حالتی دیگر دوران دهیم، آن ماده در برابر دوران متقارن باقی می‌ماند اگر اجزای تنسور سختی را نیز باید با توجه به حالت جدید دوران داد[11]

${\displaystyle c_{pqrs}=l_{pi}~l_{qj}~l_{rk}~l_{s\ell }~c_{ijk\ell }}$

که در آن ${\displaystyle l_{ab}}$ اجزای یک ماتریس متعامد دوران به نام ${\displaystyle [L]}$ است. رابطهٔ مشابه برای وارون‌ها نیز وجود دارد.

در جبر ماتریس‌ها داریم که اگر ماتریس تغییر یافته (به صورت وارون یا دوران) خود وابسته به ماتریس‌های دیگر باشد، اجزای آن خود دچار تغییر شکل می‌شوند. برای نمونه اگر:

${\displaystyle [\mathbf {e} _{i}']=[L][\mathbf {e} _{i}]}$

آنگاه

${\displaystyle C_{ij}~\epsilon _{i}~\epsilon _{j}=C_{ij}'~\epsilon '_{i}~\epsilon '_{j}~.}$

همچنین اگر ماده نسبت به ماتریس تغییر شکل ${\displaystyle [L]}$ متقارن باشد، آنگاه:

${\displaystyle C_{ij}=C'_{ij}\quad \implies \quad C_{ij}~(\epsilon _{i}~\epsilon _{j}-\epsilon '_{i}~\epsilon '_{j})=0~.}$

مواد راست‌محور

مواد راست‌محور (به انگلیسی: Orthotropic materials) دارای سه صفحهٔ راست تقارن‌اند. اگر بردارهای پایهٔ (${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}}$) بردارهای نرمال صفحهٔ تقارن باشند، بنابراین رابطه‌های تغییر دستگاه مختصات به صورت زیر وارد می‌شوند:

${\displaystyle {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}&0&0&0\\C_{12}&C_{22}&C_{23}&0&0&0\\C_{13}&C_{23}&C_{33}&0&0&0\\0&0&0&C_{44}&0&0\\0&0&0&0&C_{55}&0\\0&0&0&0&0&C_{66}\end{bmatrix}}{\begin{bmatrix}\epsilon _{1}\\\epsilon _{2}\\\epsilon _{3}\\\epsilon _{4}\\\epsilon _{5}\\\epsilon _{6}\end{bmatrix}}}$

وارون رابطهٔ بالا چنین نوشته می‌شود:[12]

${\displaystyle {\begin{bmatrix}\epsilon _{\rm {xx}}\\\epsilon _{\rm {yy}}\\\epsilon _{\rm {zz}}\\2\epsilon _{\rm {yz}}\\2\epsilon _{\rm {zx}}\\2\epsilon _{\rm {xy}}\end{bmatrix}}={\begin{bmatrix}{\tfrac {1}{E_{\rm {x}}}}&-{\tfrac {\nu _{\rm {xy}}}{E_{\rm {x}}}}&-{\tfrac {\nu _{\rm {xz}}}{E_{\rm {x}}}}&0&0&0\\-{\tfrac {\nu _{\rm {yx}}}{E_{\rm {y}}}}&{\tfrac {1}{E_{\rm {y}}}}&-{\tfrac {\nu _{\rm {yz}}}{E_{\rm {y}}}}&0&0&0\\-{\tfrac {\nu _{\rm {zx}}}{E_{\rm {z}}}}&-{\tfrac {\nu _{\rm {zy}}}{E_{\rm {z}}}}&{\tfrac {1}{E_{\rm {z}}}}&0&0&0\\0&0&0&{\tfrac {1}{G_{\rm {yz}}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{\rm {zx}}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{\rm {xy}}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{\rm {xx}}\\\sigma _{\rm {yy}}\\\sigma _{\rm {zz}}\\\sigma _{\rm {yz}}\\\sigma _{\rm {zx}}\\\sigma _{\rm {xy}}\end{bmatrix}}}$

که در آن:

${\displaystyle {E}_{\rm {i}}\,}$ مدول یانگ در طول محور ${\displaystyle i}$ است.

${\displaystyle G_{\rm {ij}}\,}$ مدول برشی در راستای ${\displaystyle j}$ در صفحه‌ای که بردار عمود بر سطحش در راستای ${\displaystyle i}$ است.

${\displaystyle \nu _{\rm {ij}}\,}$ ضریب پواسون است که برای فشردگی در راستای ${\displaystyle j}$ هنگامی که در راستای ${\displaystyle i}$ کشیدگی داشته باشیم.

در صفحهٔ تنش ${\displaystyle \sigma _{zz}=\sigma _{zx}=\sigma _{yz}=0}$ است. قانون هوک برای یک مادهٔ راست‌محور به صورت زیر در می‌آید:

${\displaystyle {\begin{bmatrix}\varepsilon _{\rm {xx}}\\\varepsilon _{\rm {yy}}\\2\varepsilon _{\rm {xy}}\end{bmatrix}}={\begin{bmatrix}{\frac {1}{E_{\rm {x}}}}&-{\frac {\nu _{\rm {xy}}}{E_{\rm {x}}}}&0\\-{\frac {\nu _{\rm {yx}}}{E_{\rm {y}}}}&{\frac {1}{E_{\rm {y}}}}&0\\0&0&{\frac {1}{G_{\rm {xy}}}}\end{bmatrix}}{\begin{bmatrix}\sigma _{\rm {xx}}\\\sigma _{\rm {yy}}\\\sigma _{\rm {xy}}\end{bmatrix}}\,.}$

وارون رابطه خواهد بود:

${\displaystyle {\begin{bmatrix}\sigma _{\rm {xx}}\\\sigma _{\rm {yy}}\\\sigma _{\rm {xy}}\end{bmatrix}}={\cfrac {1}{1-\nu _{\rm {xy}}\nu _{\rm {yx}}}}{\begin{bmatrix}E_{\rm {x}}&\nu _{\rm {xy}}E_{\rm {y}}&0\\\nu _{\rm {yx}}E_{\rm {x}}&E_{y}&0\\0&0&G_{\rm {xy}}(1-\nu _{\rm {xy}}\nu _{\rm {yx}})\end{bmatrix}}{\begin{bmatrix}\varepsilon _{\rm {xx}}\\\varepsilon _{\rm {yy}}\\2\varepsilon _{\rm {xy}}\end{bmatrix}}\,.}$

مواد همسان جانبی

یک مادهٔ همسان جانبی با چرخش نسبت به یک محور تقارن همسان باقی می‌ماند. برای چنین ماده‌ای اگر ${\displaystyle \mathbf {e} _{3}}$ محور تقارن باشد، قانون هوک چنین نوشته می‌شود:

${\displaystyle {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}&0&0&0\\C_{12}&C_{11}&C_{13}&0&0&0\\C_{13}&C_{13}&C_{33}&0&0&0\\0&0&0&C_{44}&0&0\\0&0&0&0&C_{44}&0\\0&0&0&0&0&{\tfrac {1}{2}}(C_{11}-C_{12})\end{bmatrix}}{\begin{bmatrix}\epsilon _{1}\\\epsilon _{2}\\\epsilon _{3}\\\epsilon _{4}\\\epsilon _{5}\\\epsilon _{6}\end{bmatrix}}}$

معمول است که ${\displaystyle x\equiv \mathbf {e} _{1}}$ را محور تقارن در نظر بگیرند، حال وارون رابطه چنین خواهد بود:[13]

${\displaystyle {\begin{bmatrix}\epsilon _{\rm {xx}}\\\epsilon _{\rm {yy}}\\\epsilon _{\rm {zz}}\\2\epsilon _{\rm {yz}}\\2\epsilon _{\rm {zx}}\\2\epsilon _{\rm {xy}}\end{bmatrix}}={\begin{bmatrix}{\tfrac {1}{E_{\rm {x}}}}&-{\tfrac {\nu _{\rm {xy}}}{E_{\rm {x}}}}&-{\tfrac {\nu _{\rm {xy}}}{E_{\rm {x}}}}&0&0&0\\-{\tfrac {\nu _{\rm {yx}}}{E_{\rm {y}}}}&{\tfrac {1}{E_{\rm {y}}}}&-{\tfrac {\nu _{\rm {yz}}}{E_{\rm {y}}}}&0&0&0\\-{\tfrac {\nu _{\rm {yx}}}{E_{\rm {y}}}}&-{\tfrac {\nu _{\rm {zy}}}{E_{\rm {y}}}}&{\tfrac {1}{E_{\rm {y}}}}&0&0&0\\0&0&0&{\tfrac {2(1+\nu _{\rm {yz}})}{E_{\rm {y}}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{\rm {xy}}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{\rm {xy}}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{\rm {xx}}\\\sigma _{\rm {yy}}\\\sigma _{\rm {zz}}\\\sigma _{\rm {yz}}\\\sigma _{\rm {zx}}\\\sigma _{\rm {xy}}\end{bmatrix}}}$

پایهٔ ترمودینامیکی قانون هوک

تغییر شکل‌های خطی مواد کشسان را می‌توان به مفهوم فرایند بی‌دررو نزدیک دانست. با فرض این وضعیت و برای فرایندهای شِبهِ ایستا، قانون اول ترمودینامیک برای یک حجم تغییر شکل یافته به صورت زیر گفته می‌شود:

${\displaystyle \delta W=\delta U\,}$

که در آن ${\displaystyle \delta U}$ انرژی درونی افزایش یافته و ${\displaystyle \delta W}$ کار انجام شده بوسیلهٔ نیروی خارجی است. اجزای کار را می‌توان به صورت زیر از هم جدا کرد:

${\displaystyle \delta W=\delta W_{s}+\delta W_{b}\,}$

که در آن ${\displaystyle \delta W_{s}}$ کار انجام شده بوسیلهٔ نیروی سطحی است و ${\displaystyle \delta W_{b}}$ کار انجام شده بوسیلهٔ نیروی حجمی است. اگر ${\displaystyle \delta \mathbf {u} }$ تغییرات میدان جابجایی ${\displaystyle \mathbf {u} }$ در حجم باشد؛ در نتیجه دو بخش کار خارجی به صورت زیر توضیح داده می‌شود:

${\displaystyle \delta W_{s}=\int _{\partial \Omega }\mathbf {t} \cdot \delta \mathbf {u} ~{\rm {dS}}~;~~\delta W_{b}=\int _{\Omega }\mathbf {b} \cdot \delta \mathbf {u} ~{\rm {dV}}}$

که در آن ${\displaystyle \mathbf {t} }$ بردار نیروی سطحی و ${\displaystyle \mathbf {b} }$ بردار نیروی حجمی و ${\displaystyle \Omega \,}$ نشان دهندهٔ یک حجم و ${\displaystyle \partial \Omega }$ نشانهٔ سطح آن است. حال از رابطهٔ تنش ${\displaystyle \mathbf {t} =\mathbf {n} \cdot {\boldsymbol {\sigma }}}$ (که در آن ${\displaystyle \mathbf {n} }$ بردار عمود بر سطح رو به بیرون ${\displaystyle \partial \Omega }$ است) استفاده می‌کنیم و خواهیم داشت:

${\displaystyle \delta W=\delta U=\int _{\partial \Omega }(\mathbf {n} \cdot {\boldsymbol {\sigma }})\cdot \delta \mathbf {u} ~{\rm {dS}}+\int _{\Omega }\mathbf {b} \cdot \delta \mathbf {u} ~{\rm {dV}}}$

با تبدیل انتگرال سطحی به انتگرال حجمی با استفاده از نظریهٔ دیورژانس خواهیم داشت:

${\displaystyle \delta U=\int _{\Omega }[{\boldsymbol {\nabla }}\cdot ({\boldsymbol {\sigma }}\cdot \delta \mathbf {u} )+\mathbf {b} \cdot \delta \mathbf {u} ]~{\rm {dV}}~.}$

با کاربرد تنش کوشی:

${\displaystyle {\boldsymbol {\nabla }}\cdot ({\boldsymbol {A}}\cdot \mathbf {b} )=({\boldsymbol {\nabla }}\cdot {\boldsymbol {A}})\cdot \mathbf {b} +{\tfrac {1}{2}}[{\boldsymbol {A}}^{T}:{\boldsymbol {\nabla }}\mathbf {b} +{\boldsymbol {A}}:({\boldsymbol {\nabla }}\mathbf {b} )^{T}]}$

داریم:

${\displaystyle \delta U=\int _{\Omega }[{\boldsymbol {\sigma }}:{\tfrac {1}{2}}\{{\boldsymbol {\nabla }}\delta \mathbf {u} +({\boldsymbol {\nabla }}\delta \mathbf {u} )^{T}\}+\{{\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}+\mathbf {b} \}\cdot \delta \mathbf {u} ]~{\rm {dV}}~.}$

از تعریف کرنش و معادلات تعادل بدست می‌آید که:

${\displaystyle \delta {\boldsymbol {\epsilon }}={\tfrac {1}{2}}[{\boldsymbol {\nabla }}\delta \mathbf {u} +({\boldsymbol {\nabla }}\delta \mathbf {u} )^{T}]~;~~{\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}+\mathbf {b} =\mathbf {0} ~.}$

بنابراین می‌توان نوشت:

${\displaystyle \delta U=\int _{\Omega }{\boldsymbol {\sigma }}:\delta {\boldsymbol {\epsilon }}~{\rm {dV}}}$

پس برای تغییرات چگالی انرژی درونی داریم:

${\displaystyle \delta U_{0}={\boldsymbol {\sigma }}:\delta {\boldsymbol {\epsilon }}~.}$

یک مادهٔ کشسان ماده‌ای است که در آن تمامی انرژی درونی برابر است با انرژی پتانسیل نیروهای درونی (همچنین آن را انرژی تغییر شکل‌های کشسان نیز می‌نامند) بنابراین چگالی انرژی درونی تابعی از تغییر شکل‌ها ${\displaystyle U_{0}=U_{0}({\boldsymbol {\epsilon }})}$ می‌باشد. تغییرات انرژی درونی را به صورت زیر می‌توان نوشت:

${\displaystyle \delta U_{0}={\cfrac {\partial U_{0}}{\partial {\boldsymbol {\epsilon }}}}:\delta {\boldsymbol {\epsilon }}~.}$

از آن جایی که تغییرات کرنش دلخواه است، رابطهٔ تنش - کرنش یک مادهٔ کشسان به صورت زیر داده می‌شود:

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {\partial U_{0}}{\partial {\boldsymbol {\epsilon }}}}~.}$

برای یک مادهٔ کشسان خطی، کمیت ${\displaystyle \partial U_{0}/\partial {\boldsymbol {\epsilon }}}$ یک تابع خطی از ${\displaystyle {\boldsymbol {\epsilon }}}$ است پس می‌توان آن را به شکل زیر نوشت:

${\displaystyle {\boldsymbol {\sigma }}={\mathsf {c}}:{\boldsymbol {\epsilon }}}$

که در آن ${\displaystyle {\mathsf {c}}}$ یک تنسور مرتبه چهارم از ثابت‌های ماده‌است که آن را تنسور سختی نیز می‌نامند.

یادداشت و منبع

1. والتر لوین (October 1, 1999). Hook's Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10 (ogg) (videotape) (به English). Cambridge, MA USA: MIT OCW. Event occurs at 1:21-10:10. Retrieved December 23, 2010. ...arguably the most important equation in all of Physics.
2. والتر لوین (October 1, 1999). Hook's Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10 (videotape) (به English). Cambridge, MA USA: MIT OCW. Event occurs at 10:10-16:33. Archived from the original (ogg) on 29 June 2011. Retrieved December 23, 2010.
3. The anagram was "ceiiinosssttuv", بایگانی‌شده در ۱۳ نوامبر ۲۰۱۰ توسط Wayback Machine; cf. the anagram for the Catenary, which appeared in the preceding paragraph.
4. Dieter George E. ,Mechanical Metallurgy, McGraw-Hill, New York ,1961 ,pp 16,37
5. Symon, Keith (1971). Mechanics. Addison-Wesley, Reading, MA. ISBN 0-201-07392-7.
6. Simo, J. C. and Hughes, T. J. R. , 1998, Computational Inelasticity, Springer.
7. Milton, G. W. , 2002, Theory of Composites, Cambridge University Press.
8. minor symmetries
9. major symmetries
10. دستگاهی با بردارهای یکه و دو به دو متعامد
11. Slaughter, W. S. , 2002, The Linearized Theory of Elasticity, Birkhauser
12. Boresi, A. P, Schmidt, R. J. and Sidebottom, O. M. , 1993, Advanced Mechanics of Materials, Wiley.
13. Tan, S. C. , 1994, Stress Concentrations in Laminated Composites, Technomic Publishing Company, Lancaster, PA.

• A.C. Ugural, S.K. Fenster, Advanced Strength and Applied Elasticity, 4th ed

جستارهای وابسته

• تنش (فیزیک)
• مکانیک جامدات
• ضریب پواسون
• فرم درجه دوم
• تسلیم (مهندسی)
• کشسانی

پپوند به بیرون

• استفاده از جاوا برای نمایش حرکت‌ها در قانون هوک بایگانی‌شده در ۱۸ آوریل ۲۰۰۸ توسط Wayback Machine

رابطه‌های تبدیل مدول‌ها به یکدیگر
خواص کشسانی مواد کشسان خطی همگن و همسانگرد را می‌توان با داشتن دو مدول دلخواه به طور کامل و منحصر به فردی تعیین کرد. بنابراین با در دست داشتن دو مدول و با استفاده از فرمول‌های زیر می‌توان سایر مدول‌ها را محاسبه کرد.
	${\displaystyle K=\,}$	${\displaystyle E=\,}$	${\displaystyle \lambda =\,}$	${\displaystyle G=\,}$	${\displaystyle \nu =\,}$	${\displaystyle M=\,}$	توضیحات
${\displaystyle (K,\,E)}$	${\displaystyle K}$	${\displaystyle E}$	${\displaystyle {\tfrac {3K(3K-E)}{9K-E}}}$	${\displaystyle {\tfrac {3KE}{9K-E}}}$	${\displaystyle {\tfrac {3K-E}{6K}}}$	${\displaystyle {\tfrac {3K(3K+E)}{9K-E}}}$
${\displaystyle (K,\,\lambda )}$	${\displaystyle K}$	${\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}}$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {3(K-\lambda )}{2}}}$	${\displaystyle {\tfrac {\lambda }{3K-\lambda }}}$	${\displaystyle 3K-2\lambda \,}$
${\displaystyle (K,\,G)}$	${\displaystyle K}$	${\displaystyle {\tfrac {9KG}{3K+G}}}$	${\displaystyle K-{\tfrac {2G}{3}}}$	${\displaystyle G}$	${\displaystyle {\tfrac {3K-2G}{2(3K+G)}}}$	${\displaystyle K+{\tfrac {4G}{3}}}$
${\displaystyle (K,\,\nu )}$	${\displaystyle K}$	${\displaystyle 3K(1-2\nu )\,}$	${\displaystyle {\tfrac {3K\nu }{1+\nu }}}$	${\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}}$	${\displaystyle \nu }$	${\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}}$
${\displaystyle (K,\,M)}$	${\displaystyle K}$	${\displaystyle {\tfrac {9K(M-K)}{3K+M}}}$	${\displaystyle {\tfrac {3K-M}{2}}}$	${\displaystyle {\tfrac {3(M-K)}{4}}}$	${\displaystyle {\tfrac {3K-M}{3K+M}}}$	${\displaystyle M}$
${\displaystyle (E,\,\lambda )}$	${\displaystyle {\tfrac {E+3\lambda +R}{6}}}$	${\displaystyle E}$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {E-3\lambda +R}{4}}}$	${\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}}$	${\displaystyle {\tfrac {E-\lambda +R}{2}}}$	${\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}}$
${\displaystyle (E,\,G)}$	${\displaystyle {\tfrac {EG}{3(3G-E)}}}$	${\displaystyle E}$	${\displaystyle {\tfrac {G(E-2G)}{3G-E}}}$	${\displaystyle G}$	${\displaystyle {\tfrac {E}{2G}}-1}$	${\displaystyle {\tfrac {G(4G-E)}{3G-E}}}$
${\displaystyle (E,\,\nu )}$	${\displaystyle {\tfrac {E}{3(1-2\nu )}}}$	${\displaystyle E}$	${\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}}$	${\displaystyle {\tfrac {E}{2(1+\nu )}}}$	${\displaystyle \nu }$	${\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}}$
${\displaystyle (E,\,M)}$	${\displaystyle {\tfrac {3M-E+S}{6}}}$	${\displaystyle E}$	${\displaystyle {\tfrac {M-E+S}{4}}}$	${\displaystyle {\tfrac {3M+E-S}{8}}}$	${\displaystyle {\tfrac {E-M+S}{4M}}}$	${\displaystyle M}$	${\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}}$ There are two valid solutions. The plus sign leads to ${\displaystyle \nu \geq 0}$. The minus sign leads to ${\displaystyle \nu \leq 0}$.
${\displaystyle (\lambda ,\,G)}$	${\displaystyle \lambda +{\tfrac {2G}{3}}}$	${\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}}$	${\displaystyle \lambda }$	${\displaystyle G}$	${\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}}$	${\displaystyle \lambda +2G\,}$
${\displaystyle (\lambda ,\,\nu )}$	${\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}}$	${\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}}$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}}$	${\displaystyle \nu }$	${\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}}$	Cannot be used when ${\displaystyle \nu =0\Leftrightarrow \lambda =0}$
${\displaystyle (\lambda ,\,M)}$	${\displaystyle {\tfrac {M+2\lambda }{3}}}$	${\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}}$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {M-\lambda }{2}}}$	${\displaystyle {\tfrac {\lambda }{M+\lambda }}}$	${\displaystyle M}$
${\displaystyle (G,\,\nu )}$	${\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}}$	${\displaystyle 2G(1+\nu )\,}$	${\displaystyle {\tfrac {2G\nu }{1-2\nu }}}$	${\displaystyle G}$	${\displaystyle \nu }$	${\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}}$
${\displaystyle (G,\,M)}$	${\displaystyle M-{\tfrac {4G}{3}}}$	${\displaystyle {\tfrac {G(3M-4G)}{M-G}}}$	${\displaystyle M-2G\,}$	${\displaystyle G}$	${\displaystyle {\tfrac {M-2G}{2M-2G}}}$	${\displaystyle M}$
${\displaystyle (\nu ,\,M)}$	${\displaystyle {\tfrac {M(1+\nu )}{3(1-\nu )}}}$	${\displaystyle {\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}}$	${\displaystyle {\tfrac {M\nu }{1-\nu }}}$	${\displaystyle {\tfrac {M(1-2\nu )}{2(1-\nu )}}}$	${\displaystyle \nu }$	${\displaystyle M}$