خیز (مهندسی)
در مهندسی، خیز (به انگلیسی: Deflection)، به میزان جابه جایی یک عضو سازه ای مانند تیر، تحت اثر بار اعمال شده به آن (به دلیل تغییر شکلی که در سازه ایجاد میشود) گفته میشود که ممکن است این خیز به یک زاویه یا طول نسبت داده شود.
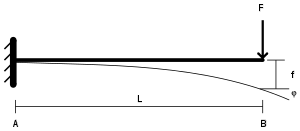
اندازهٔ خیز یک تیر که تحت اثر بار قرار گرفته را میتوان با انتگرالگیری از تابعی که به صورت ریاضی، شیب عضو بارگذاری شده را توصیف میکند، محاسبه کرد.
فرمولهای استاندارد برای محاسبهٔ خیز تیرهای رایج که به صورت گسسته بارگذاری شدهاند وجود دارد.
همچنین روشهای دیگری مانند "کار مجازی"، "انتگرالگیری مستقیم"، "روش کاستیگلیانو"، "روش ماکولی" و "روش سختی مستقیم" برای محاسبهٔ خیز تیرهای تحت بارگذاری گسسته یا پیوسته وجود دارد. خیز یک تیر معمولی از معادلهٔ تیر "اویلر - برنولی" محاسبه میشود در حالی که خیز یک عضو صفحه ای یا پوسته ای با استفاده از نظریهی"صفحه یا پوسته" محاسبه میشود.
نمونه ای از کاربردهای خیز در ساخت و ساز ساختمان است. معماران و مهندسان مواد را برای کاربردهای مختلف انتخاب میکنند بنابراین جنس و مصالح تیرهای اسکلت ساختمان، بر اساس خیز و عوامل دیگر انتخاب میشوند.
خیز تیر برای انواع بارگذاریها
تیرها میتوانند از لحاظ هندسه و ترکیب باهم بسیار متفاوت باشند. به عنوان مثال، تیر ممکن است مستقیم یا خمیده باشد. ممکن است دارای سطح مقطع ثابت یا متغیر باشد. ممکن است از نظر جنس کاملاً یکنواخت یا از مواد مختلفی(کامپوزیت) تشکیل شده باشد.
برخی از موارد بالا تجزیه و تحلیل را دشوار میکند، اما بسیاری از کاربردهای مهندسی مواردی را شامل میشوند که چندان پیچیده نیستند.
بنابراین تجزیه و تحلیل آسان است اگر:
- -تیر مستقیم و دارای تغییرات جزئی است.
- -تیر فقط تغییر شکل الاستیک خطی را تجربه میکند.
- -تیر باریک است (نسبت طول به ارتفاع از ۱۰ بیشتر است).
- -فقط خیزهای کوچک در نظر گرفته شدهاست (حداکثر خیز کمتر از ۱/۱۰ طول تیر).
در این حالت، معادله حاکم بر خیز تیر () میتواند تقریباً برابر عبارت زیر باشد:
که در آن عبارت سمت چپ، مشتق دوم معادلهٔ خیز تیر به صورت تابعی از x (فاصلهٔ هر نقطه از تیر از ابتدای تیر) است، مدول الاستیسیته است ، ممان اینرسی سطح مقطع نسبت به محور خنثی و معادلهٔ گشتاور (لنگر) خمشی در تیر است است.
این رابطه را معادله دیفرانسیل منحنی الاستیک و جملهٔ EI را صلابت خمشی میگویند.
علاوه بر این، اگر تیر مستقیم و یکنواخت باشد و بار گستردهٔ q به آن اعمال شود، عبارت فوق را میتوان به صورت زیر نوشت:
این معادله برای انواع بارگذاری و شرایط مرزی قابل حل است. تعدادی مثال ساده در زیر آورده شدهاست:
فرمول بیان شده تقریباً برای پرتوهای بلند، باریک، همگن، منشوری با انحرافهای کوچک و خاصیت الاستیک خطی است. تحت این محدودیتها، تقریبها با ۵٪ خطا نسبت به واقعیت نتایج به دست میآیند.
تیرهای کانسیلر (طره ای یا یک سر گیردار)
تیرهای یک سرگیردار یک انتهای ثابت دارند، به طوری که شیب و خیز در انتهای آن باید صفر باشد.
۱_تیرهای با بارگذاری متمرکز در انتهای آزاد
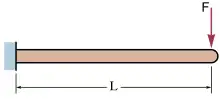
خیز الاستیک و شیب (برحسب رادیان) در انتهای آزاد تیر (مطابق تصویر بالا) میتوان از روابط زیر محاسبه کرد:[1]
که در این روابط:
- = نیرویی که به صورت متمرکز به انتهای تیر وارد میشود.
- = طول تیر
- = مدول الاستیسیته
- = ممان اینرسی سطح مقطع تیر
توجه داشته باشید که اگر طول تیر دو برابر شود، میزان خیز تیر در انتها هشت برابر میشود. همچنین خیز و شیب در هر نقطه از تیر یک سر گیردار تحت بارگذاری متمرکز، از روابط زیر محاسبه میشود:[1]
توجه: در (انتهای آزاد تیر)، معادلات و با معادلات فوق برای خیز و شیب نقطهٔ B یکسان هستند.
۲_تیرهای با بارگذاری گسترده
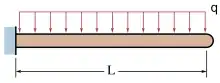
معادلات خیز و شیب، در انتهای آزاد این تیر که تحت بارگذاری گسترده قرار دارد به صورت زیر میباشد:[1]
که در این روابط:
- = بار یکنواخت روی تیر (نیرو در واحد طول)
- = طول تیر
- = مدول الاستیسیته
- = ممان اینرسی سطح مقطع
همچنین خیز و شیب در هر نقطه از تیر یک سرگیردار تحت بارگزاری گسترده از روابط زیر محاسبه میشود:[1]
تیرهای با تکیه گاه ساده
قسمتی از این تیرها که روی تکیه گاه ساده قرار دارند دچار خیز نمیشوند و خیز در این نقاط از تیر، صفر میباشد.
۱_تیرهای با بارگذاری مرکزی (نیروی مرکزی)
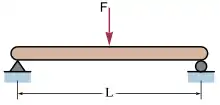
خیز الاستیک (در نقطه میانی C) یک تیر، که نیرو در مرکز آن قرار دارد و توسط دو تکیه گاه ساده پشتیبانی میشود به صورت زیر است:[1]
که در این رابطه:
- = نیرویی که در مرکز تیر قرار دارد
- = طول تیر بین تکیه گاهها
- = مدول الاستیسیته
- = ممان اینرسی سطح مقطع
خیز در هر نقطه (x) از تیر با تکیه گاه ساده از رابطهٔ زیر محاسبه میشود:[1]
برای
۲_تیرهای با بارگذاری خارج از مرکز (نیروی خارج از مرکز)
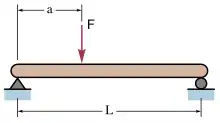
حداکثر خیز الاستیک در تیری که توسط دو تکیه گاه ساده پشتیبانی میشود، در یک فاصله a (فاصلهٔ نیروی وارد شده تا نزدیکترین تکیه گاه) اتفاق میافتد که به صورت زیر محاسبه میشود:[1]
که در این رابطه:
- = نیرویی که روی تیر قرار دارد اما مرکزی نیست
- = طول تیر بین تکیه گاهها
- = مدول الاستیسیته
- = ممان اینرسی سطح مقطع
- = فاصلهٔ بار وارد شده تا نزدیکترین تکیه گاه (یعنی)
۳_تیرهای با بارگذاری گسترده
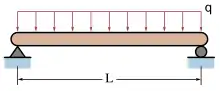
خیز الاستیک (در نقطه میانی C) بر روی تیری با تکیه گاههای ساده که تحت بار گستردهٔ q قرار دارد به صورت زیر محاسبه میشود:[1]
که در این رابطه:
- = بار یکنواخت روی تیر (نیرو در واحد طول)
- = طول تیر
- = مدول الاستیسیته
- = ممان اینرسی سطح مقطع
خیز در هر نقطه (x) از تیر با تکیه گاه ساده که تحت بار گسترده قرار دارد از رابطهٔ زیر محاسبه میشود:[1]
تغییرات طول تیر
تغییر طول تیر بهطور کلی در سازهها ناچیز است، اما میتوان با ادغام تابع شیب و تابع خیز تیر به راحتی و با استفاده از رابطهٔ زیر آن را محاسبه کرد:
که در این رابطه:
- = تغییر طول (همیشه منفی)
- = تابع شیب (اولین مشتق از )
- [2]
اگر تیر یکنواخت باشد و خیز در هر نقطه از تیر معلوم باشد، این تغییر طول میتواند بدون دانستن سایر خصوصیات تیر محاسبه شود.
واحدها
فرمولهای ارائه شده در بالا نیاز به استفاده از مجموعه ای ثابت از واحدها دارد. بیشتر محاسبات در سیستم بینالمللی واحدها (SI) یا سیستم US انجام میشود، اگرچه سیستمهای واحد دیگری نیز وجود دارد.
سیستم بینالمللی (SI)
- نیرو: نیوتن ()
طول: متر ()
- مدول الاستیسیته:
- ممان اینرسی:
سیستم US
- نیرو: پوند ()
- طول: اینچ ()
- مدول الاستیسیته:
- ممان اینرسی:
سیستمهای دیگر
گاهی ممکن است از واحدهای دیگر نیز استفاده شود. به عنوان مثال، گاهی اوقات واحد کیلوگرم () برای اندازهگیری بارها استفاده میشود. در چنین حالتی، مدول الاستیسیته به این صورت است .
جستارهای وابسته
منابع
- Gere, James M.; Goodno, Barry J. Mechanics of Materials (Eighth ed.). pp. 1083–1087. ISBN 978-1-111-57773-5.
- Roark's Formulas for Stress and Strain, 8th Edition Eq 8.1-14