دستگاه مختصات گرانیگاهی
در هندسه، دستگاه مختصات گرانیگاهی، دستگاهی است که در آن یک نقطه، گرانیگاه مجموعهای از جرمها است؛ جرمهایی که در گوشههای یک سادک (مانند مثلث، هرم و...) قرار میگیرند. مختصات گرانیگاهی گونهای از مختصات همگن است. این دستگاه اولین بار در سال ۱۸۲۷ توسط آگوست فردینانند موبیوس معرفی شد.
تعریف
فرض کنید گوشههای یک چندوجهی در فضای برداری A باشد؛ اگر برای برخی نقاط در فضای A داشته باشیم:
و حداقل یکی از ناصفر باشد، آنگاه میتوانیم بگوییم که ضرایب () مختصات گرانیگاهی نسبت به هستند. مختصات خود گوشهها عبارت است از . مختصات گرانیگاهی یکتا نیستند. برای هر b ناصفر، () نیز مختصات گرانیگاهی p است.
وقتی مکان نقاط در دستگاه مختصات منفی نیست، نقطهای مانند در یک پوش محدب از قرار میگیرد؛ این همان چند وجهی (در فضای چندبعدی دلخواه) است که آن نقاط را به عنوان گوشههای خود (رأسهایش) در بر میگیرد.
مختصات گرانیگاهی در مثلثها
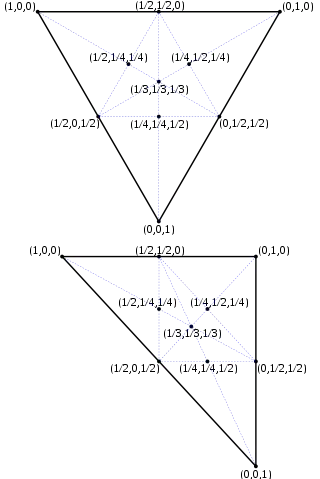
در مورد یک مثلث، مختصات گرانیگاهی را با نام مختصات مساحتی نیز میشناسند. چرا که مختصات نقطهٔ P نسبت به مثلث ABC، از نسبت (علامتدار) مساحتهای PBC و PCA و PAB نسبت به مثلث اصلی ABC تعیین میشود. مختصات مساحتی و مختصات سهخطی برای هدفهای مشابه در هندسه کاربرد دارند.
مختصات گرانیگاهی یا مساحتی در کاربردهای مهندسی مانند زیردامنههای مثلثی، بسیار مورد استفاده قرار میگیرند. همچنین استفاده از این مختصات برآورد انتگرال را بسیار سادهتر میکند؛ در جدول انتگرال گاوسی نیز معمولاً از این مختصات استفاده میشود.
ابتدا مثلث T را با سه گوشهٔ و و در نظر میگیریم هر نقطهای مانند که روی مثلث قرار دارد را میتوان به صورت مجموع وزنی سه گوشهٔ مثلث نوشت:
که و و مختصات مساحتیاند (معمولاً با نمایش داده میشوند.) البته با این فرض که:
پس
با توجه به گفتههای بالا میتوان نتیجه گرفت که انتگرال تابعی مانند روی T برابر خواهد بود با:
توجه داشته باشید که در عبارت بالا، درون یابی خطی وجود دارد. در واقع مختصات مساحتی این اجازه را میدهد که از درونیابی خطی در تمام نقاط مثلث استفاده کنیم به شرطی که مقدار تابع در تمام گوشههای مثلث معلوم باشد.
تبدیل به مختصات گرانیگاهی
نقطهٔ داده شدهٔ درون یک مثلث را میتوان با مختصات گرانیگاهی و و نیز نشان داد. برداری مانند را که در دستگاه مختصات دکارتی قرار دارد، میتوان به وسیلهٔ گوشههای یک مثلث (, , ) در مختصات گرانیگاهی به شکل زیر بازنویسی کرد:
با جایگذاری در عبارت بالا خواهیم داشت:
پس از مرتبسازی میشود:
این نگاشت خطی را میتوان به صورت کوتاهتر بازنویسی کرد:
که در آن بردار مختصات گرانیگاهی است و بردار مختصات دکارتی است و یک ماتریس به شکل زیر است:
ماتریس یک ماتریس وارون پذیر است، چون و خود مستقل خطی اند (اگر چنین نبود، آنگاه و , و هم راستا بودند و هرگز یک مثلث تشکیل نمیدادند.). حال میتوان عبارت بالا را به شکل زیر بازنویسی کرد:
پیدا کردن مختصات گرانیگاهی آنگاه که یک ماتریس 2×2 باشد کار آسانی خواهد بود.
در نهایت، عبارت ریاضی لازم برای بازنویسی در مختصات گرانیگاهی به صورت زیر خواهد بود:
تشخیص اینکه آیا یک نقطه درون مثلث قرار دارد یا خیر
چون مختصات کرانیگاهی یک تبدیل خطی از مختصات کارتزین است، پس باید، مقادیر در بین اضلاع و روی سطح مثلث به صورت خطی تغییر کند. اگر نقطهای درون مثلث قرار داشته باشد تمام مقادیر در مختصات گرانیگاهی در بازهٔ باز (0,1) جای میگیرد؛ اگر یک نقطه بر روی لبههای مثلث (اضلاع) قرار داشته باشد حداقل یکی از اعداد مختصات صفر خواهد بود در حالی که دیگر اعداد در بازهٔ بستهٔ [0,1] جای دارند.
به عبارت دیگر:
- نقطهٔ درون مثلث قرار دارد اگر و تنها اگر .
- اگر چنین نبود، بر لبه (ضلع) یا نوک (رأس) مثلث قرار دارد اگر .
- اگر چنین نبود، بیرون از مثلث است.
درونیابی روی یک شبکهٔ نامنظم مثلثی
مختصات گرانیگاهی امکان مناسبی برای درونیابی یک تابع روی یک شبکهٔ نامنظم یا شبکه فراهم میکند؛ با این فرض که مقدار تابع در تمامی گوشههای آن شبکه معلوم باشد.
برای درونیابی تابعی مانند در نقطهای مانند ، در مرحلهٔ اول پیدا میکنیم که آن نقطه در کدام یک از جزءهای مثلثی شبکه قرار دارد آنگاه مقدار تابع را در سه گوش آن مثلث پیدا میکنیم و بعد نقطهٔ را به مختصات گرانیگاهی آن مثلث منتقل میکنیم. اگر آنگاه، نقطه درون مثلث یا بر روی لبهٔ آن قرار دارد (در بخش پیشین توضیح داده شد). حال مقدار را به شکل زیر درونیابی میکنیم.
این درونیابی خطی به صورت خودکار یکه شدهاست، چون: .
مختصات گرانیگاهی روی چهاروجهی
مختصات گرانیگاهی را میتوان به آسانی در سه بعد گسترش داد. سادک سه بعدی، یک چهاروجهی یا یک چندوجهی است که چهار رویهٔ مثلثی و چهار گوشه دارد. در اینجا باید اولین گوشهٔ به مختصات گرانیگاهی نگاشته شود، به همین ترتیب برای و ...
در این حالت نیز، باز با یک تبدیل خطی روبرو هستیم، باید روندی که در بالا برای مثلث توضیح داده شد را گسترش داد و آن را با توجه به چهاروجهی برای انتقال نقطهای مانند بازنویسی کرد.
که در آن ماتریسی 3×3 است:
مسئلهٔ پیدا کردن مختصات گرانیگاهی به یک ماتریس 3×3 کاهش یافت. از مختصات گرانیگاهی برای دانستن اینکه آیا یک نقطه درون یک حجم چهاروجهی قرار میگیرد یا خیر یا درونیابی یک تابع در فضای یک شبکه با خانههای چهاروجهی کاربرد دارد. شبکههای با خانههای چهاروجهی معمولاً در روش اجزاء محدود کاربرد دارد؛ چون استفاده از مختصات گرانیگاهی، درونیابی سه بعدی را بسیار آسان میکند.
منابع
مشارکتکنندگان ویکیپدیا. «Barycentric coordinate system». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۲ ژوئن ۲۰۱۱.
پیوند به بیرون
- The uses of homogeneous barycentric coordinates in plane euclidean geometry
- Barycentric Coordinates – a collection of scientific papers about (generalized) barycentric coordinates
- Barycentric coordinates: A Curious Application (solving the «three glasses» problem) at cut-the-knot