پوش محدب

در ریاضیات، پوشش محدب(Convex hull) یا لفاف محدب مجموعه از نقاط در صفحه اقلیدسی یا فضای اقلیدسی، کوچکترین مجموعه محدبی است که شامل این مجموعه می‌باشد. به عنوان مثال، هنگامی که X یک زیر مجموعه محدود از نقاط در صفحه است، پوشش محدب ممکن است به شکل نواری نشان داده شود که در اطراف X کشیده شده است. برای این که تصور بهتری از پوش محدب به دست آورید، نقاط صفحه را مانند میخ‌هایی در نظر بگیرید که به دیوار کوبیده شده‌اند. حال کش تنگی را در نظر بگیرید که همه میخ‌ها را احاطه کرده است. در این صورت پوش محدب نقاط شکلی خواهد بود که کش به خود می‌گیرد. مسئله یافتن پوشش محدب مجموعه نامحدود از نقاط در صفحه یا دیگر فضاهای اقلیدسی یکی از مسائل اساسی در هندسه محاسباتی است.

پوش محدب: مثال کِش.

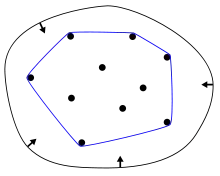
الگوریتم‌هایی جهت یافتن پوش محدب

ما در این قسمت دو الگوریتم برای یافتن پوش محدب مجموعه‌ای از نقاط ارائه خواهیم داد. خروجی هر دوی این الگوریتمها رئوس پوش محدب در جهت پادساعتگرد خواهد بود.

الگوریتم پیمایش گراهام

مجموعه نقاط ورودی را Q در نظر بگیرید. الگوریتم پیمایش گراهام(به انگلیسی: Grham's Scan) با در نظر گرفتن یک پشته از نقاط کاندید، پوش محدب را پیدا می‌کند(ما این پشته راs می نامیم). در این روش همه نقاط یک بار در پشته اضافه می‌شوند و نقاطی که بر روی محیط پوش محدب قرار ندارند در نهایت از پشته حذف می‌شوند و در نتیجه در پایان الگوریتم مجموعه نقاطی که در s قرار دارند همان رئوس پوش محدب است.

شبه کد زیر الگوریتم پیمایش گراهام را پیاده‌سازی می‌کند.

1 let p[0] be the point in Q with the minimum y-coordinate
or the left most such point in case of a tie
2 letp[1],p[2],...,p[m] be the remaining points in Q,
sorted by polar angle in counterclockwise order around p[0]
(if more than one point has the same angle, remove all but
the one that is farthest from p0)
3 PUSH(p[0], S)
4 PUSH(p[0],S)
5 PUSH(p[2],S)
6 for i ← 3 to m
7 do while the angle formed by points NEXT-TO-TOP(S), TOP(S),
and p[i] makes a nonleft turn
8 do POP(S)
9 PUSH(p[i],S)
10 return S

در خط 1 این کد ابتدا از بین نقاط Q نقطه‌ای را که کمترین مختصه y را دارد انتخاب می‌کند و آن را ${\displaystyle p_{0}}$ می نامد. و سپس در خط 2 نقاط باقی‌مانده را نسبت به زاویهٔ قطبی آن‌ها نسبت به ${\displaystyle p_{0}}$ مرتب می‌کند. در این مرتب‌سازی در صورتی که دو نقطه زاویه برابری داشتند آن نقطه‌ای را که فاصله کمتری تا ${\displaystyle p_{0}}$ دارد را حذف می‌کند و در پایان نقاط مرتب شده را درآرایهٔ p قرار می‌دهد و نقاط ${\displaystyle p_{0}}$ و ${\displaystyle p_{1}}$ و ${\displaystyle p_{2}}$ را به پشته s اضافه می‌کند. در خطوط 6 تا 10 که در واقع قسمت اصلی الگوریتم است یک بار کل نقاط s را پرمایش می‌کند. در هر مرحله به ازای هر نقطه ${\displaystyle p_{i}}$ تا زمانی که زاویه بین دو نفر آخر پشته s و ${\displaystyle p_{i}}$ بیش از 180 درجه باشد نفر آخر پشته را حذف می‌کند. در زیر پیاده‌سازی این الگوریتم در زبان C# آمده‌است.

 
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace GrahamScan
{
    class GrahamScan
    {
        const int TURN_LEFT = 1;
        const int TURN_RIGHT = -1;
        const int TURN_NONE = 0;
        public int turn(Point p, Point q, Point r)
        {
            return ((q.getX() - p.getX()) * (r.getY() - p.getY())
 - (r.getX() - p.getX()) * (q.getY() - p.getY())).CompareTo(0);
        }

        public void keepLeft(List<Point> hull, Point r)
        {
            while (hull.Count> 1 &&
 turn(hull[hull.Count - 2], hull[hull.Count - 1], r) != TURN_LEFT)
            {
                //Removing Point ({0}, {1}) because turning right
                hull.RemoveAt(hull.Count - 1);
            }
            if (hull.Count == 0 || hull[hull.Count - 1] != r)
            {
                //Adding Point ({0}, {1})
                hull.Add(r);
            }    
        }

        public double getAngle(Point p1, Point p2)
        {
            float xDiff = p2.getX() - p1.getX();
            float yDiff = p2.getY() - p1.getY();
            return Math.Atan2(yDiff, xDiff) * 180.0 / Math.PI;
        }

        public List<Point> MergeSort(Point p0, List<Point> arrPoint)
        {
            if (arrPoint.Count == 1)
            {
                return arrPoint;
            }
            List<Point> arrSortedInt = new List<Point>();
            int middle = (int)arrPoint.Count / 2;
            List<Point> leftArray = arrPoint.GetRange(0, middle);
            List<Point> rightArray = arrPoint.GetRange(middle, arrPoint.Count - middle);
            leftArray = MergeSort(p0, leftArray);
            rightArray = MergeSort(p0, rightArray);
            int leftptr = 0;
            int rightptr = 0;
            for (int i = 0; i <leftArray.Count + rightArray.Count; i++)
            {
                if (leftptr == leftArray.Count)
                {
                    arrSortedInt.Add(rightArray[rightptr]);
                    rightptr++;
                }
                else if (rightptr == rightArray.Count)
                {
                    arrSortedInt.Add(leftArray[leftptr]);
                    leftptr++;
                }
                else if (getAngle(p0, leftArray[leftptr]) <getAngle(p0, rightArray[rightptr]))
                {
                    arrSortedInt.Add(leftArray[leftptr]);
                    leftptr++;
                }
                else
                {
                    arrSortedInt.Add(rightArray[rightptr]);
                    rightptr++;
                }
            }
            return arrSortedInt;
        }

        public List<Point> convexHull(List<Point> points)
        {
            //let p[0] be the point in Q with the minimum y-coordinate
        
            Point p0 = null;
            foreach (Point value in points)
            {
                if (p0 == null)
                    p0 = value;
                else
                {
                    if (p0.getY()> value.getY())
                        p0 = value;
                }
            }

            //the left most such point in case of a tie
            List<Point> order = new List<Point>();
            order.Add(p0);
            foreach (Point value in points)
            {
                if (p0 != value)
                    order.Add(value);
            }
            //sorted by polar angle in counterclockwise order around p[0]
            //if more than one point has the same angle, remove it
            order = MergeSort(p0, order);           
            //add first 3  point
            List<Point> result = new List<Point>();
            result.Add(p0);
            result.Add(order[0]);
            result.Add(order[1]);
            //remove 2 element form order list
            order.RemoveAt(0);
            order.RemoveAt(0);
            //Current Convex Hull           
            foreach (Point value in order)
            {
                keepLeft(result, value);
            }

            return result;
        }

       
    }
}

پیچیدگی الگوریتم پیمایش گراهام

در این جا نشان می‌دهیم که زمان اجرای الگوریتم گراهام از ${\displaystyle O(nlogn)\,\!}$ است. خط 1 الگوریتم زمان ${\displaystyle O(n)\,\!}$ را مصرف می‌کند چون یک جستجوی ساده بر روی نقاط است. خط 2 الگوریتم را در صورتی که با الگوریتم مرتب‌سازی ادغامی پیاده‌سازی کنیم در زمان ${\displaystyle O(nlogn)\,\!}$ اجرا شود. در قسمت‌های بعد نیز ما فقط با پشته s کار می‌کنیم و چون هر نقطه دقیقاً یک بار به پشته اضافه می‌شد و حداکثر یک بار از آن حذف می‌شود پس بقیه کد نیز در زمان ${\displaystyle O(n)\,\!}$ اجرا می‌شود پس در کل الگوریتم پیمایش گراهام در زمان ${\displaystyle O(nlogn)\,\!}$ اجرا می‌شود.

الگوریتمJarvis's march

نمونه‌ای از فرایند اجرای الگوریتمJarvis's march.

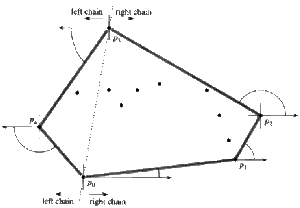
Jarvis's march از روشی به نام بسته‌بندی بسته(به انگلیسی: package wrapping)برای یافتن پوش محدب مجموعه Q از نقاط صفحه استفاده می‌کند. این الگوریتم به این صورت عمل می‌کند که ابتدا نقاط را بر اساس مختص Yشان مرتب کرده و در صورتی که Y برابری داشته باشد بر اساس X آن‌ها را مرتب می‌کند و در آرایهٔ P نگه می‌دارد. در این صورت نقطه ${\displaystyle p[0]}$ حتماً یکی از نقاط پوش محدب است. پس آن را در یک آرایه به نام C وارد می‌کند. حال از بین سایر نقاط نقطه‌ای را پیدا می‌کند که کمترین زاویهٔ قطبی را وابسته به نقطه ${\displaystyle p[0]}$ دارد و آن را نیز در آرایهٔ C اضافه می‌کند و همین فرایند را برای نقطه ${\displaystyle p[1]}$ تکرار می‌کند تا این که به آخرین نقطه آرایهٔ p برسد. به مجموعه کنونی که در C قرار دارد زنجیره راست (به انگلیسی: right chain) می‌گوییم. برای ساختن زنجیره چپ (به انگلیسی: left chain) از ${\displaystyle p[n]}$ (آخرین نقطهٔ مجموعه P)شروع کردهودوباره نقطه‌ای را انتخاب می‌کنیم که نسبت به ${\displaystyle p[n]}$ کمترین زاویه قطبی را دارد اما این بار نسبت به قسمت منفی محور X و آن نقطه را نیز به مجموعهٔ C اضافه می‌کنیم و این کار را برای این نقطه تکرار می‌کنیم تا به نقطه ${\displaystyle p[0]}$ اولیه بر گردیم. در این صورت مجموعه C ساخته شده همان پوش محدب مورد نظر است.

پیچیدگی الگوریتم

این الگوریتم از ${\displaystyle O(nh)\,\!}$است که در آن n تعداد نقاط است و h تعداد رئوس پوش محدب است. زیرا به ازای هر کدام از رئوس پوش محدب یک بار هر یک از نقاط را با عملی از ${\displaystyle O(1)\,\!}$ چک می‌کنیم.

منابع

• UDI MANBER, دانشگاه آریزونا, مقدمه‌ای بر الگوریتم‌ها
• توماس اچ کورمن, Charles E. Leiserson, رونالد ریوست and کلیفورد استین (2001), مقدمه‌ای بر الگوریتم‌ها (second ed.), MIT Press and McGraw-Hill, ISBN 0-262-53196-8