فضای آفین
در ریاضیات، یک فضای آفین، ساختاری هندسی است که برخی از خصوصیات فضاهای اقلیدسی را به گونه ای که مستقل از مفهوم فاصله و اندازه گیری زاویه باشد، تعمیم می دهد، به گونه ای که تنها خواص توازی (موازی بودن) و نسبت طول پاره خط های موازی با هم حفظ شوند.
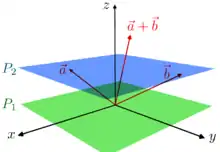
در یک فضای آفین، هیچ نقطه تمایز یافته ای به عنوان مبدأ فضا وجود ندارد. لذا، هیچ برداری مبدأ ثابت ندشته و هیچ برداری را نمی توان به طور منحصر به فردی به یک نقطه نسبت داد. در یک فضای برداری، تنها بردار های جابجایی وجود دارند که به آن ها بردار های انتقال یا به طور ساده تر انتقال بین نقاط فضا گفته می شود.[1] لذا، تفاضل نقاط فضا معنادار خواهد بود و منجر به تولید بردار انتقال می گردد، اما جمع کردن نقاط فضا بی معنی خواهد بود. بنابر این، می توان با جمع کردن یک بردار انتقال به یک نقطه، به نقاط جدید رسید.
هر فضای برداری را می توان به عنوان یک فضای آفین دید. این امر با فراموش کردن نقش ویژه ای که بردار صفر در فضای برداری بازی می کند فراهم می گردد. در این حالت، عناصر فضای برداری را می توان یا به صورت نقاط فضای آفین دید، یا به صورت بردار های جابجایی یا "انتقال ها". زمانی که یک بردار صفر را به عنوان نقطه بنگیرم، به آن مبدأ هم گفته می شود. اضافه کردن یک بردار ثابت به عناصر یک زیر فضای خطی از یک فضای برداری، زیر فضای آفین را تولید خواهد کرد. اغلب گفته می شود که این زیر فضای آفین از طریق انتقال (دور کردن آن از مبدأ) یک زیر فضای خطی با کمک بردار انقال بدست آمده است. در ابعاد نامتناهی، چنین زیرفضای آفینی، مجموعه جواب دستگاه خطی ناهمگن خواهد بود. بردار های انتقال برای آن فضای آفین هم جواب های متناضر به دسگاه همگن خطی خواهد بود که خود زیر فضایی خطی می باشند. در مقایسه، زیرفضاهای خطی همیشه شامل مبدأ آن فضای برداریست.
بعد یک فضای آفین به صورت بعد فضای برداری انتقالات آن تعریف می شود. یک فضای آفین از بعد یک را خط آفینی می گویند. یک فضای آفین از بعد 2 همان صفحه آفین است. یک زیر فضای آفین از بعد n-1 در یک فضای آفین از فضای برداری از بعد n را نیز ابرصفحه ی آفین نامند.
پانویس
- معمولاً از کلمه "انتقال" برای اشاره به "بردار انتقال" استفاده می شود، به گونه ای که این امر ممکن است موجب سردرگمی خواننده گردد، چرا که دوران هم نوع خاصی از انتقال است.
منابع
- Berger, Marcel (1984), "Affine spaces", Problems in Geometry, Springer-Verlag, ISBN 978-0-387-90971-4
- Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
- Cameron, Peter J. (1991), Projective and polar spaces, QMW Maths Notes, 13, London: Queen Mary and Westfield College School of Mathematical Sciences, MR 1153019
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
- Affine space, Dolgachev and Shirokov
- Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 978-0-387-90244-9. Zbl 0367.14001.
- Nomizu, K.; Sasaki, S. (1994), Affine Differential Geometry (New ed.), Cambridge University Press, ISBN 978-0-521-44177-3
- Snapper, Ernst; Troyer, Robert J. (1989), Metric Affine Geometry (Dover edition, first published in 1989 ed.), Dover Publications, ISBN 0-486-66108-3
- Tarrida, Agusti R. (2011), "Affine spaces", Affine Maps, Euclidean Motions and Quadrics, Springer, ISBN 978-0-85729-709-9
- مشارکتکنندگان ویکیپدیا. «Affine Space». در دانشنامهٔ ویکیپدیای انگلیسی.