فضای اقلیدسی

فضای برداری ${\displaystyle \mathbb {R} ^{k}}$ با ضرب داخلی و نرم ${\displaystyle \|\mathbf {x} \|={\bigg (}\sum _{i=1}^{k}x_{i}^{2}{\bigg )}^{1/2}}$ که ${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{k})\in \mathbb {R} ^{k}}$، را فضای اقلیدسی k بعدی می‌نامیم.

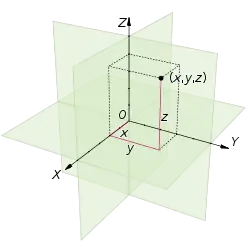
مختصات هر نقطه در فضای اقلیدسی سه بعدی، با سه‌تایی مرتب نشان داده می‌شود.

${\displaystyle \mathbb {R} }$، فضای اقلیدسی یک‌بعدی یا همان خط حقیقی است. ${\displaystyle \mathbb {R} \times \mathbb {R} }$ یا ${\displaystyle \mathbb {R} ^{2}}$ نیز فضای اقلیدسی دو بعدی است که به آن صفحه اقلیدسی یا دستگاه مختصات دکارتی می‌گوییم. با تعمیم این مفاهیم فضای اقلیدسی nبعدی یا ${\displaystyle \mathbb {R} ^{n}}$ و به همین ترتیب فضای اقلیدسی بینهایت بعدی، ${\displaystyle \mathbb {R} ^{\omega }}$ تعریف می‌شوند.

فضاهای با بعد بالاتر در زمینه‌هایی مانند نسبیت، مکانیک آماری و مکانیک کوانتمی کاربرد دارند. در مکانیک کوانتمی حتی فضاهای با بعد نامتناهی نیز کاربرد دارند.

تعاریف و اصطلاحات

یک نقطه در فضای دو بعدی عبارت است از جفت مرتبی از عددهای حقیقی مانند ${\displaystyle (x_{1},x_{2})}$. به همین طریق یک نقطه در فضای سه بعدی، سه‌تایی مرتبی از عددهای حقیقی مانند ${\displaystyle (x_{1},x_{2},x_{3})}$ است؛ بنابراین می‌توان nتایی مرتبی از عددهای حقیقی مانند ${\displaystyle (x_{1},x_{2},\ldots ,x_{n})}$ را به عنوان نقطه‌ای در فضای nبعدی در نظر گرفت.

منابع

• مصاحب، غلامحسین (۱۳۸۱). آنالیز ریاضی. اول. تهران: امیرکبیر. شابک ۹۶۴-۰۰-۰۶۳۰-۰.
• رودین، والتر (۱۳۸۵). اصول آنالیز ریاضی. ترجمهٔ علی‌اکبر عالم‌زاده. تهران: علمی و فنی. شابک ۹۶۴-۶۲۱۵-۰۰-۹.
• اپوستل، تام م. (۱۳۵۹). آنالیز ریاضی. ترجمهٔ علی‌اکبر عالم‌زاده. تهران: دانشگاه صنعتی شریف.
• مانکرز، جیمز ر. (۱۳۸۹). توپولوژی، نخستین درس. ترجمهٔ جواد لالی و دیگران. تهران: مرکز نشر دانشگاهی. شابک ۹۷۸-۹۶۴-۰۱-۰۲۸۳-۱.