تابع شبه‌محدب

در ریاضیات تابع شبه‌کوژ یا تابع شبه‌محدب به تابعی گفته می‌شود که کلیهٔ مجموعه‌های سطوح زیرین آن مجموعهٔ کوژ باشند.[1] به زبان ساده‌تر در یک تابع شبه‌کوژ، بیشینهٔ تابع روی هر بازهٔ دلخواه از دامنهٔ آن یکی از نقاط ابتدایی یا انتهایی بازه است.

یک تابع شبه‌کوژ که کوژ نیست.

یک تابع که شبه‌کوژ نیست: مجموعهٔ نقاطی از دامنهٔ تابع که که مقدارشان کمتر از خط نقطه‌چین قرمز است، اجتماع دو بازهٔ قرمزرنگ هستند. این اجتماع یک مجموعهٔ کوژ نیست.

تابع چگالی احتمال یک توزیع نرمال شبه‌کاو است، اما کاو نیست.

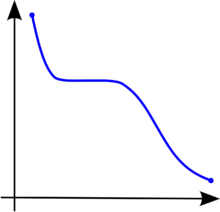
یک تابع شبه خطی هم شبه‌کاو و هم شبه‌کوژ است.

مثالی از نمودار یک تابع که روی اعداد حقیقی مثبت، هم کاو است و هم شبه‌کوژ.

هر تابع شبه‌کوژی لزوماً کوژ نیست، اما همهٔ توابع کوژ، شبه‌کوژ هستند.

به بیان ریاضی اگر ${\displaystyle f:S\to \mathbb {R} }$ روی مجموعهٔ کوژ S تعریف شده باشد، آنگاه f یک تابع شبه‌کوژ است اگر به ازای هر ${\displaystyle x,y\in S}$ و ${\displaystyle \lambda \in [0,1]}$ داشته باشیم:[2]

${\displaystyle f(\lambda x+(1-\lambda )y)\leq \max {\big \{}f(x),f(y){\big \}}.}$

در صورتی که در این نابرابری به جای ${\displaystyle \leq }$ از ${\displaystyle <}$ استفاده شود، تعریف تابع اکیداً شبه‌کوژ به دست می‌آید.

ویژگی‌ها

• منفی یک تابع شبه‌کوژ یک تابع شبه‌کاو است.
• هر کمینهٔ موضعی یک تابع شبه‌کوژ، کمینهٔ سراسری آن نیز هست، اما لزوماً منحصر به فرد نیست.[3]
• اگر ${\displaystyle f}$ یک تابع شبه‌کوژ تعریف‌شده روی مجموعهٔ کوژِ ${\displaystyle S\subseteq \Re ^{n}}$ باشد و ${\displaystyle S^{*}}$ مجموعهٔ کلیهٔ نقاط کمینهٔ سراسری ${\displaystyle f}$، آنگاه ${\displaystyle S^{*}}$ یک مجموعهٔ کوژ است.[4]

کاربردها

توابع شبه‌کوژ در بررسی نظریه‌های تصمیم‌گیری اقتصادی کاربرد دارند.[5]

جستارهای وابسته

• بهینه‌سازی محدب
• مسائل بهینه‌سازی شبه‌محدب

پانویس

1. dos Santos Gromicho and dos Santos Gromicho, Quasiconvex Optimization and Location Theory, 28.
2. Pavel, Optimal Control of Differential Equations, 43.
3. Udriste, Convex Functions and Optimization Methods on Riemannian Manifolds, 100.
4. Cambini and Martein, Generalized Convexity and Optimization: Theory and Applications, 26.
5. Quasiconcavity and quasiconvexity.

منابع

• "Quasiconcavity and quasiconvexity". U of T. 2014. Retrieved 2014-10-31.
• Pavel, N.H. (1994). Optimal Control of Differential Equations. Lecture Notes in Pure and Applied Mathematics. Taylor & Francis. ISBN 978-0-8247-9234-3. Retrieved 2014-10-31.
• Udriste, C. (1994). Convex Functions and Optimization Methods on Riemannian Manifolds. Linguistica Computazionale. Springer. ISBN 978-0-7923-3002-8. Retrieved 2014-10-31.
• dos Santos Gromicho, J.A.; dos Santos Gromicho, J.A. (1998). Quasiconvex Optimization and Location Theory. Applied Optimization. Springer. ISBN 978-0-7923-4694-4. Retrieved 2014-10-31.
• Cambini, A.; Martein, L. (2008). Generalized Convexity and Optimization: Theory and Applications. Lecture Notes in Economics and Mathematical Systems. Springer. ISBN 978-3-540-70876-6. Retrieved 2014-10-31.
• Wikipedia contributors, "Quasiconvex function," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Quasiconvex_function&oldid=627237125 (accessed October 31, 2014).