عرق‌چین (هندسه)

در هندسه عرق‌چین (به انگلیسی: Spherical cap) قطعه‌ای از کره است که با برش کره توسط صفحه ایجاد می‌شود. اگر صفحه از مرکز کره عبور کند شکل حاصل نیم‌کره خواهد بود.

نمونه‌ای از عرق‌چین به رنگ آبی (و عرق‌چین دیگری به رنگ قرمز).

مدل سه‌بعدی عرق‌چین.

حجم و مساحت رویه

حجم و مساحت عرق‌چین با استفاده از ترکیب کمیت‌های زیر محاسبه می‌شود:

• ${\displaystyle r}$ شعاع کره
• ${\displaystyle a}$ شعاع قاعدهٔ عرق‌چین
• ${\displaystyle h}$ ارتفاع عرق‌چین
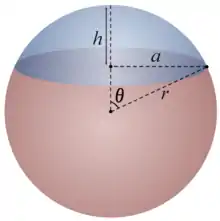
• ${\displaystyle \theta }$ زاویه قطبی بین شعاعی که از مرکز کره به راس عرق‌چین (بالاترین نقطهٔ عرق‌چین) می‌رود و لبه قرص تشکیل دهندهٔ پایهٔ عرق‌چین است.

تمام کمیت‌های بالا در شکل نشان داده شده‌اند.

	با استفاده از ${\displaystyle r}$ و ${\displaystyle h}$	با استفاده از ${\displaystyle a}$ و ${\displaystyle h}$	با استفاده از ${\displaystyle r}$ و ${\displaystyle \theta }$
حجم	${\displaystyle V={\frac {\pi h^{2}}{3}}(3r-h)}$[1]	${\displaystyle V={\frac {1}{6}}\pi h(3a^{2}+h^{2})}$	${\displaystyle V={\frac {\pi }{3}}r^{3}(2+\cos \theta )(1-\cos \theta )^{2}}$
مساحت	${\displaystyle A=2\pi rh}$	${\displaystyle A=\pi (a^{2}+h^{2})}$	${\displaystyle A=2\pi r^{2}(1-\cos \theta )}$

اگر ${\displaystyle \phi }$ نشان دهندهٔ عرض جغرافیایی لبهٔ دیسک باشد آنگاه ${\displaystyle \theta +\phi =\pi /2=90^{\circ }\,}$

توجه کنید که تمام روابط بالا آن‌هایی که برا اساس ${\displaystyle r}$ و ${\displaystyle h}$ نوشته شده‌اند را می‌توان بر اساس ${\displaystyle a}$ و ${\displaystyle r}$ نوشت (با استفاده از قضیه فیثاغورس)

${\displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2}\,,}$

پس

${\displaystyle r={\frac {a^{2}+h^{2}}{2h}}\,.}$

با جایگزین کردن این فرمول‌ها:

${\displaystyle V={\frac {\pi h^{2}}{3}}\left({\frac {3a^{2}+3h^{2}}{2h}}-h\right)={\frac {1}{6}}\pi h(3a^{2}+h^{2})\,,}$

${\displaystyle A=2\pi {\frac {(a^{2}+h^{2})}{2h}}h=\pi (a^{2}+h^{2})\,.}$

پیدا کردن حجم و مساحت با استفاده از حسابان

با دوران ناحیهٔ سبز رنگ حول محور xها عرق‌چینی با شعاع ${\displaystyle r}$ و ارتفاع ${\displaystyle h}$ ایجاد می‌شود.

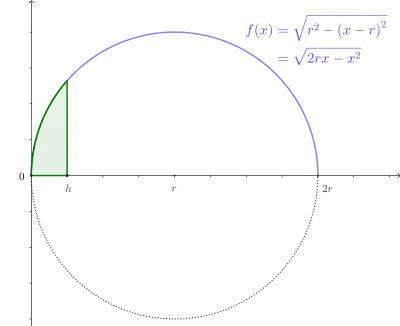
حجم و مساحت را با استفاده از دوران تابع می‌توان حساب کرد.

${\displaystyle f(x)={\sqrt {r^{2}-(x-r)^{2}}}={\sqrt {2rx-x^{2}}}}$

فرمول سطح دورانی برای پیدا کردن مساحت استفاده می‌کنیم.

${\displaystyle A=2\pi \int _{0}^{h}f(x){\sqrt {1+f'(x)^{2}}}\,dx}$

مشتق ${\displaystyle f}$ برابر است با:

${\displaystyle f'(x)={\frac {r-x}{\sqrt {2rx-x^{2}}}}}$

پس

${\displaystyle 1+f'(x)^{2}={\frac {r^{2}}{2rx-x^{2}}}}$

پس فرمول مساحت رویه برابر است با:

${\displaystyle A=2\pi \int _{0}^{h}{\sqrt {2rx-x^{2}}}{\sqrt {\frac {r^{2}}{2rx-x^{2}}}}\,dx=2\pi \int _{0}^{h}r\,dx=2\pi r\left[x\right]_{0}^{h}=2\pi rh}$

از فرمول جسم دورانی برای حجم استفاده می‌کنیم پس:

${\displaystyle V=\pi \int _{0}^{h}f(x)^{2}\,dx=\pi \int _{0}^{h}(2rx-x^{2})\,dx=\pi \left[rx^{2}-{\frac {1}{3}}x^{3}\right]_{0}^{h}={\frac {\pi h^{2}}{3}}(3r-h)}$

کاربردها

پیدا کردن حجم اجتماع دو کرهٔ متقاطع

حجم حاصل از اجتماع دو کرهٔ متقاطع با شعاع‌های ${\displaystyle r_{1}}$ و ${\displaystyle r_{2}}$ برابر است با:[2]

${\displaystyle V=V^{(1)}-V^{(2)}\,,}$

که

${\displaystyle V^{(1)}={\frac {4\pi }{3}}r_{1}^{3}+{\frac {4\pi }{3}}r_{2}^{3}}$

که برابر با جمع حجم‌های دو کره جدا از هم است و

${\displaystyle V^{(2)}={\frac {\pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{\frac {\pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}$

که برابر حجم دو عرق‌چین تشکیل دهندهی ناحیهٔ مشترک بین دو کره است. اگر ${\displaystyle d\leq r_{1}+r_{2}}$ فاصلهٔ بین مرکزهای دو کره باشد با پیدا کردن مقادیر ${\displaystyle h_{1}}$ و ${\displaystyle h_{2}}$ داریم:[3][4]

${\displaystyle V^{(2)}={\frac {\pi }{12d}}(r_{1}+r_{2}-d)^{2}\left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}\right)\,.}$

مساحت‌های رویه‌های متقاطع

فرض کنید شعاع‌های دو کرهٔ متقاطع ${\displaystyle r_{1}}$ و ${\displaystyle r_{2}}$ و مرکز دو کره به اندازهٔ ${\displaystyle d}$ از هم فاصله دارند. اگر شرط زیر برقرار باشد آن‌ها همدیگر را قطع می‌کنند.

${\displaystyle |r_{1}-r_{2}|\leq d\leq r_{1}+r_{2}}$

با استفاده از قانون کسینوس‌ها زاویهٔ قطبی عرق‌چین در کرهٔ با شعاع ${\displaystyle r_{1}}$ برابر مقدار زیر است:

${\displaystyle \cos \theta ={\frac {r_{1}^{2}-r_{2}^{2}+d^{2}}{2r_{1}d}}}$

با کمک مقدار بالا مساحت عرق‌چین سمت دایره ${\displaystyle r_{1}}$ را پیدا می‌کنیم.

${\displaystyle A_{1}=2\pi r_{1}^{2}\left(1+{\frac {r_{2}^{2}-r_{1}^{2}-d^{2}}{2r_{1}d}}\right)}$

رویهٔ محدود شده با دو قرص موازی

مساحت رویهٔ قطعهٔ کره (عرق‌چینی که با دو صفحه محدود شده) برابر با اختلاف مساحت دو عرق‌چینی است که هر یک از صفحه‌ها به‌طور جدا گانه به وجود می‌آورند. شعاع کره برابر ${\displaystyle r}$ و ارتفاع‌های دو عرق‌چین ${\displaystyle h_{1}}$ و ${\displaystyle h_{2}}$ است پس سطح برابر با:

${\displaystyle A=2\pi r|h_{1}-h_{2}|\,,}$

یا با استفاده از مختصات کروی با عرض‌های ${\displaystyle \phi _{1}}$ و ${\displaystyle \phi _{2}}$ ، مساحت رویه بدین قرار است:[5]

${\displaystyle A=2\pi r^{2}|\sin \phi _{1}-\sin \phi _{2}|\,,}$

مثلاً فرض کنید زمین کره ای به شعاع 6371 km است مساحت رویهٔ قطب (مدار قطبی در عرض جغرافیایی ۶۶٫۵۶° قرار دارد در اوت 2016[6]) باید 2${\displaystyle \pi }$·6371²|sin ۹۰° − sin 66.56°| = 21.04 million km², or 0.5·|sin ۹۰° − sin 66.56°| = ۴٫۱۲۵٪ از مساحت کل زمین باشد.

همچنین این فرمول نشان می‌دهد که نصف مساحت زمین در ناحیهٔ بین عرض جغرافیایی ۳۰° شمالی و ۳۰° جنوبی قرار دارد.

جستارهای وابسته

• قطعه دایره - مشابه دو بعدی عرق‌چین
• قطعهٔ کره
• قطاع کره
• گوهٔ کره

منابع

1. Polyanin, Andrei D; Manzhirov, Alexander V. (2006), Handbook of Mathematics for Engineers and Scientists, CRC Press, p. 69, ISBN 978-1-58488-502-3
2. Connolly, Michael L. (1985). "Computation of molecular volume". Journal of the American Chemical Society. 107 (5): 1118–1124. doi:10.1021/ja00291a006.
3. Pavani, R.; Ranghino, G. (1982). "A method to compute the volume of a molecule". Computers & Chemistry. 6 (3): 133–135. doi:10.1016/0097-8485(82)80006-5.
4. Bondi, A. (1964). "Van der Waals volumes and radii". The Journal of Physical Chemistry. 68 (3): 441–451. doi:10.1021/j100785a001.
5. Scott E. Donaldson, Stanley G. Siegel (2001). Successful Software Development. ISBN 978-0-13-086826-8. Retrieved 29 August 2016.
6. "Obliquity of the Ecliptic (Eps Mean)". Neoprogrammics.com. Retrieved 2014-05-13.

مطالعه بیشتر

• Richmond, Timothy J. (1984). "Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect". Journal of Molecular Biology. 178: 63–89. doi:10.1016/0022-2836(84)90231-6. PMID 6548264.
• Lustig, Rolf (1986). "Geometry of four hard fused spheres in an arbitrary spatial configuration". Molecular Physics. 59: 195–207. Bibcode:1986MolPh..59..195L. doi:10.1080/00268978600102011.
• Gibson, K. D.; Scheraga, Harold A. (1987). "Volume of the intersection of three spheres of unequal size: a simplified formula". The Journal of Physical Chemistry. 91: 4121–4122. doi:10.1021/j100299a035.
• Gibson, K. D.; Scheraga, Harold A. (1987). "Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii". Molecular Physics. 62: 1247–1265. Bibcode:1987MolPh..62.1247G. doi:10.1080/00268978700102951.
• Petitjean, Michel (1994). "On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects". Journal of Computational Chemistry. 15: 507–523. doi:10.1002/jcc.540150504.
• Grant, J. A.; Pickup, B. T. (1995). "A Gaussian description of molecular shape". The Journal of Physical Chemistry. 99: 3503–3510. doi:10.1021/j100011a016.
• Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). "ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations". Computer Physics Communications. 165 (1): 59–96. Bibcode:2005CoPhC.165...59B. doi:10.1016/j.cpc.2004.08.002.

پیوند به بیرون

• Weisstein, Eric W. "Spherical cap". MathWorld. Derivation and some additional formulas.
• Online calculator for spherical cap volume and area.