فرایندهای تصمیم‌گیری مارکوف

فرایندهای تصمیم‌گیری مارکوف (به انگلیسی: Markov decision process) (به اختصار: MDPs) یک چارچوب ریاضی است برای مدل‌سازی تصمیم‌گیری در شرایطی که نتایج تا حدودی تصادفی و تا حدودی تحت کنترل یک تصمیم‌گیر است. MDPs برای مطالعه طیف گسترده‌ای از مسائل بهینه سازی که از طریق برنامه‌نویسی پویا و تقویت یادگیری حل می‌شوند مفید است. حداقل از اوایل ۱۹۵۰ میلادی MDPs شناخته شده‌است (cf. Bellman 1957). هسته اصلی پژوهش در فرایندهای تصمیم‌گیری مارکوف حاصل کتاب رونالد هوارد است که در سال ۱۹۶۰ تحت عنوان «برنامه‌نویسی پویا و فرایندهای مارکف» منتشر شد.[1] فرایندهای تصمیم‌گیری مارکوف در طیف گسترده‌ای از رشته‌ها از جمله رباتیک، اقتصاد و تولید استفاده می‌شود.

به‌طور دقیق تر، فرایندهای تصمیم‌گیری مارکوف، فرایندهای کنترل تصادفی زمان گسسته است. در هر گام، فرایند در حالت ${\displaystyle s}$ است و تصمیم‌گیر اقدام (عمل) ${\displaystyle a}$ را انتخاب می‌کند. پاسخ فرایند، رفتن به حالت جدید ${\displaystyle s}$ (در گام بعدی) به‌طور تصادفی و همچنین دادن پاداش R_a(s,s') به تصمیم‌گیر است ${\displaystyle R_{a}(s,s')}$.

تعریف

مثال ساده MDP با سه حالت و دو عمل

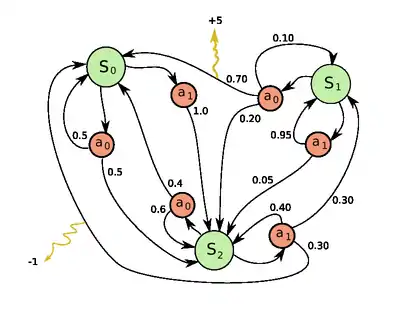
فرایندهای تصمیم‌گیری مارکوف شامل پنج عنصر ${\displaystyle (S,A,P_{\cdot }(\cdot ,\cdot ),R_{\cdot }(\cdot ,\cdot ),\gamma )}$ است که در ادامه شرح داده می‌شود

• ${\displaystyle S}$ مجموعه متناهی (شمارش پذیر) حالت‌ها است.
• ${\displaystyle A}$ مجموعه متناهی عمل‌ها است. به‌طور جایگزین ${\displaystyle A_{s}}$ مجموعه متناهی از عمل‌ها است که حالت ${\displaystyle s}$
• ${\displaystyle P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ احتمال این که اقدام ${\displaystyle a}$ در حالت ${\displaystyle s}$ و در زمان ${\displaystyle t}$ منجر به حالت ${\displaystyle s'}$ در زمان ${\displaystyle t+1}$
• ${\displaystyle R_{a}(s,s')}$ پاداش فوری (یا انتظار پاداش فوری) است که به علت رفتن از حالت ${\displaystyle s'}$ به حالت ${\displaystyle s}$
• ${\displaystyle \gamma \in [0,1]}$ ضریب کاهش است که نشان دهنده تفاوت ارزش پاداش آتی با پاداش فعلی است.

مسئله

مسئله اصلی در MDPs پیدا کردن یک «سیاست» برای تصمیم‌گیر است. یافتن یک تابع مشخص عمل ${\displaystyle \pi }$ که تصمیم‌گیر در هنگامی که در حالت s است انتخاب کند ${\displaystyle s}$. توجه داشته باشید که که افزودن یک سیاست ثابت به فرایندهای تصمیم‌گیری مارکوف منجر به یک زنجیره مارکوف می‌شود.

هدف انتخاب یک سیاست ${\displaystyle \pi }$ که جهت به حداکثر رساندن برخی مجموع پاداش تصادفی است.

${\displaystyle \sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}}$     (زمانی که ${\displaystyle a_{t}=\pi (s_{t})}$)

که در آن ${\displaystyle \ \gamma \ }$ این ضریب کاهش و ${\displaystyle 0\leq \ \gamma \ <1}$ است. (به عنوان مثال ${\displaystyle \gamma =1/(1+r)}$ زمانی که ضریب کاهش r است) ${\displaystyle \gamma }$ به‌طور معمول نزدیک به ۱ است.

به دلیل خاصیت مارکوف، سیاست بهینه برای یک مسئله خاص را می‌توان به عنوان یک تابع از ${\displaystyle s}$ نوشت

الگوریتم

MDPs را می‌توان با برنامه‌ریزی خطی یا برنامه‌نویسی پویا حل کرد.

تعمیم و گسترش

فرایندهای تصمیم‌گیری مارکوف یک بازی تصادفی با تنها یک بازیکن است.

مشاهده پذیری جزئی

در راه حل بالا فرض می‌شود که وقتی عمل انتخاب می‌شود که حالت ${\displaystyle s}$ شناخته شده باشد؛ در غیر این صورت ${\displaystyle \pi (s)}$ را نمی‌توان حساب کرد. زمانی که این فرض درست نیست مسئله فرایندهای تصمیم‌گیری مارکوف با مشاهده پذیری جزئی یا POMDP نامیده می‌شود.

یادگیری تقویتی

اگر احتمالات یا پاداش مشخص نباشد مسئله به عنوان یادگیری تقویتی شناخته می‌شود (Sutton & Barto 1998).

یادگیری اتوماتا

یکی دیگر از کاربردهای MDP یادگیری ماشین با نام یادگیری اوتوماتا شناخته می‌شود. این هم یک نوع از یادگیری تقویتی است اگر محیط به شیوه تصادفی باشد. [2]

تفسیر نظریه رده‌ها

غیر از پاداش، فرایندهای تصمیم‌گیری مارکوف ${\displaystyle (S,A,P)}$ می‌توان به عنوان نظریه رده‌ها درک کرد.

در این روش پردازش‌های تصمیم‌گیری مارکوف می‌تواند تعمیم از monoids (دسته‌ها با یک شی) را به دلخواه دسته‌بندی کنید. یکی می‌توانید تماس بگیرید و نتیجه ${\displaystyle ({\mathcal {C}},F:{\mathcal {C}}\to \mathbf {Dist} )}$ یک متن وابسته به پردازش‌های تصمیم‌گیری مارکوف روندچرا که در حال حرکت از یک شیء به دیگری در ${\displaystyle {\mathcal {C}}}$ تغییرات در این مجموعه موجود اقدامات و مجموعه‌ای از امکان متحده است.

فرایندهای تصمیم‌گیری مارکوف فازی (FDMPs)

در MDPs سیاست بهینه سیاستی است که جمع پاداش‌های آتی را به حداکثرمی‌رساند؛ بنابراین سیاست بهینه شامل چندین عمل است که متعلق به مجموعه متناهی از اعمال است. در فرایندهای تصمیم‌گیری مارکوف فازی (FDMPs) ابتدا تابع ارزش با فرض غیر فازی بودن محاسبه می‌شود؛ سپس توسط یک سیستم استنتاج فازی سیاست مطلوب استخراج می‌شود. به عبارت دیگر تابع ارزش تابع به عنوان یک ورودی برای سیستم استنتاج فازی استفاده شده‌است و سیاست مطلوب، خروجی سیستم استنتاج فازی است.[3]

یادداشت

1. Howard 1960.
2. Narendra & Thathachar 1989.
3. Fakoor, Mahdi; Kosari, Amirreza; Jafarzadeh, Mohsen (2016). "Humanoid robot path planning with fuzzy Markov decision processes". Journal of Applied Research and Technology. doi:10.1016/j.jart.2016.06.006.