مسئله نیوتون-پیپس

مسئلهٔ نیوتن-پیپس عنوان مسئله‌ای است که ساموئل پیپس _که ظاهراً شخصی قمار باز بوده‌است_ در نامه ای طولانی که به ایزاک نیوتن می‌نویسد از نیوتن می‌خواهد که برایش حل کند.[1]مسئله ای که مطرح می‌کند این است که کدام یک از گزاره‌های زیر بیشترین احتمال را دارد:

1. پرتاب کردن ۶ تاس عادلانه و مشاهدهٔ حداقل یک شش
2. پرتاب کردن ۱۲ تاس عادلانه و مشاهدهٔ حداقل دو شش
3. پرتاب کردن ۱۸ تاس عادلانه و مشاهدهٔ حداقل سه شش

پیپس در ابتدا تصور می‌کرد که احتمال وقوع گزارهٔ سوم از همه بیشتر است ولی نیوتن اثبات کرد که احتمال وقوع گزارهٔ اول از همه بیشتر است.

راه حل

متغیر تصادفی‌های ۳ گزاره بالا را به ترتیب A و B و C نام‌گذاری می‌کنیم. حال برای بدست آوردن احتمال‌های خواسته شده می‌توانیم از دو روش استفاده کنیم.

روش اول:

${\displaystyle P(A)=1-\left({\frac {5}{6}}\right)^{6}={\frac {31031}{46656}}\approx 0.6651\,,}$

${\displaystyle P(B)=1-\sum _{x=0}^{1}{\binom {12}{x}}\left({\frac {1}{6}}\right)^{x}\left({\frac {5}{6}}\right)^{12-x}={\frac {1346704211}{2176782336}}\approx 0.6187\,,}$

${\displaystyle P(C)=1-\sum _{x=0}^{2}{\binom {18}{x}}\left({\frac {1}{6}}\right)^{x}\left({\frac {5}{6}}\right)^{18-x}={\frac {15166600495229}{25389989167104}}\approx 0.5973\,.}$

در این روش از اصل متمم استفاده کرده‌ایم. روش دوم استفاده از توزیع دوجمله ای است که آن هم به جواب مشابه می‌رسد.[2]

این مسئله را می‌توان در حالت کلی تری مطرح کرد: احتمال این که 6n تاس عادلانه بریزیم و حداقل n عدد شش ببینیم. اگر متغیر تصادفی وقوع این اتفاق را N بگیریم احتمال وقوع N می‌شود:

${\displaystyle P(N)=1-\sum _{x=0}^{n-1}{\binom {6n}{x}}\left({\frac {1}{6}}\right)^{x}\left({\frac {5}{6}}\right)^{6n-x}\,}$

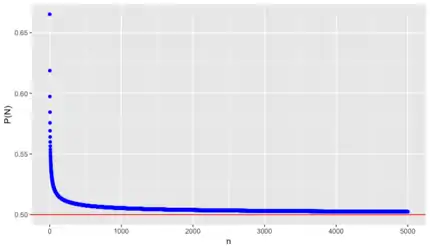
که وقتی n به بینهایت میل کند این احتمال به صورت نزولی اکید به ۱/۲ میل می‌کند.

کد R مسئله

کد R، نمودار (P(N بر حسب n با استفاده از کتابخانهٔ ggplot2 :

library(ggplot2)
xVec <- c(1:5000)
y <- sapply(xVec , function(x) pbinom(x-1 , 6*x , p = 1/6 , lower.tail = F))
x[1]
data <- data.frame(x = xVec , y = y)
ggplot() + geom_point(data = data , aes(x = x , y = y) , color = 'blue')  +
  geom_hline(yintercept = 0.5 , color = 'red') +  xlab('n') + ylab('P(N)')

نمودار حاصل :

توضیح نیوتن

نیوتن بعد از آن که مسئله را به‌درستی برای پیپس حل کرد برای آن که به پیپس شهود دهد که چرا احتمال وقوع A از B و C بیشتر است، به او گفت که تاس‌های B و C را به دسته‌های ۶ تایی تقسیم کند حال A وقتی رخ می‌دهد که یک تاس در بین ۶ تاس شش بیاید در حالی که برای B و C در هر کدام از دسته‌های ۶ تایی شان باید این اتفاق بیفتد. اما خودش هم می‌دانست که این صحبت دقیق نیست زیرا که ممکن است در یک دسته دو عدد ۶ بیاید و به همین دلیل مسئله را حل نمی‌کند.

تعمیم مسئله

بعد از فکر کردن بر روی این مسئله مسئله ای که به ذهن می‌رسد این است که اگر n عدد تاس نه لزوماً عادلانه داشته باشیم که احتمال آمدن ۶ برای آن‌ها p باشد و هر کدام از تاس‌ها نتیجه ش از بقیه مستقل باشد باز هم حرف‌هایی که زدیم درست است یا نه.

تعریف می‌کنیم : ${\displaystyle P(r\geq k;n,p)}$احتمال آن که حداقل k بار ۶ آمده باشد. حال اگر ${\displaystyle \nu _{1},\nu _{2}}$دو عدد طبیعی باشند که ${\displaystyle \nu _{1}\leq \nu _{2}}$آیا ${\displaystyle P(r\geq \nu _{1}k;\nu _{1}n,p)}$بزرگ‌تر مساوی از ${\displaystyle P(r\geq \nu _{2}k;\nu _{2}n,p)}$برای تمام n و k و p هست؟ (به وضوح سؤالی که در ابتدا مطرح کردیم حالت خاصی از این سؤال است)

جواب ثابتی برای این سؤال وجود ندارد و جواب این مسئله کاملاً بستگی به n , p , k دارد. با این وجود یک سری از فرم‌های مسئله که جواب ثابت دارند را مثال می‌زنیم:

• اگر ${\displaystyle k_{1},k_{2},n}$اعداد طبیعی باشند و ${\displaystyle k_{1}<k_{2}}$نتیجه می‌دهد: ${\displaystyle P(r\geq k_{1};k_{1}n,{\frac {1}{n}})>P(r\geq k_{2};k_{2}n,{\frac {1}{n}})}$
• اگر ${\displaystyle k,n_{1},n_{2}}$اعداد طبیعی مثبت باشند و ${\displaystyle n_{1}<n_{2}}$نتیجه می‌دهد: ${\displaystyle P(r\geq k;kn_{1},{\frac {1}{n_{1}}})>P(r\geq k;kn_{2},{\frac {1}{n_{2}}})}$
• اگر ${\displaystyle \nu _{1},\nu _{2},n,k}$اعداد طبیعی باشند و ${\displaystyle \nu _{1}\leq \nu _{2},k\leq n,p\in [0,1]}$نتیجه می‌دهد: ${\displaystyle P(r=\nu _{1}k;\nu _{1}n,p)\geq P(r=\nu _{2}k;\nu _{2}n,p)}$

اگر همین متغیر تصادفی‌های A,B،C که همان ابتدا تعریف کردیم را برای تاسی که احتمال ۶ آمدن آن P است دوباره بخواهیم سورت کنیم در ابتدا وقتی از P = ۰ شروع می‌کنیم احتمال وقوع A تا یک نقطه ای از همه بیشتر است و بعد از آن نقطه احتمال وقوع C از همه بیشتر می‌شود تا P=1.[3]

منابع

1. "Newton and Pepys". www.datagenetics.com. Retrieved 2018-11-08.
2. «Two ways to solve the Newton - Pepys problem - Abrazolica». www.exstrom.com. دریافت‌شده در ۲۰۱۸-۱۱-۰۸.
3. "Newton–Pepys problem". Wikipedia. 2018-10-06.