مکانیک مولکولی
مکانیک مولکولی از مکانیک کلاسیک برای مدلسازی سیستمهای مولکولی استفاده میکند. تقریب بورن-اوپنهایمر معتبر قرض میشود و انرژی بالقوه همه سیستمها به عنوان تابعی از مختصات هستهها با استفاده از میادین نیرو محاسبه میشود. مکانیک مولکولی میتواند برای مطالعه سیستمهای مولکولی متفاوت از نظر اندازه و پیچیدگی، سیستمهای بیولوژیکی کوچک تا بزرگ یا مجموعهها یا خوشههای مواد با هزاران تا میلیونها اتم استفاده شود.
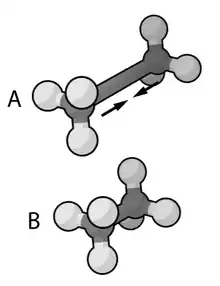
روشهای مکانیک مولکولی اتمی دارای خصوصیات زیر است:
- هر اتم به عنوان یک ذره شبیهسازی میشود
- به هر ذره یک شعاع اختصاص داده میشود (بهطور معمول شعاع ون در والس)، قطبش پذیری، و یک بار خالص ثابت (عموماً از محاسبات کوانتومی و / یا آزمایش تجربی) گرفته میشود.
- برهم کنشهای پیوندی به عنوان فنرهای با فاصله تعادل برابر با طول پیوند تجربی یا محاسبه شده در نظر گرفته میشوند
تنوع پیش زمینههای محاسباتی ممکن در این زمینه زیاد است. به عنوان مثال، بسیاری از شبیهسازیها در طول تاریخ از یک نمایش اتم واحد استفاده کردهاند که در آن هر ترمینال گروه متیل یا واحد متیلن میانی به عنوان یک ذره در نظر گرفته میشود، و سیستمهای پروتئینی بزرگ معمولاً با استفاده از یک مدل تسیحوار یا زنجیر وار شبیهسازی میشوند که دو یا چهار ذره در هر اسید آمینه به یک زنجیر اختصاص مییابد.
حالات تابعی
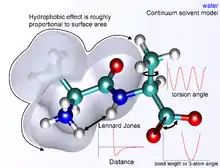
فرض تابعی زیر که به عنوان یک تابع پتانسیل بینا اتمی یا میدان نیرو در شیمی نامیده میشود، انرژی پتانسیل سیستم مولکولی (E) را در یک ساختار معین محاسبه میکند که حاصل جمع انرژی عبارات منفرد انرژی است.
که در آن اجزای سهم کووالانسی و غیر کووالانسی با تجمیع عبارات منفرد انرژی به شکل زیر آورده شدهاند:
شکل دقیق تابعی از تابع پتانسیل یا میدان نیرو بستگی به برنامه شبیهسازی خاص مورد استفاده دارد. بهطور کلی بخشهای پیوند و زاویه به عنوان پتانسیلهای هارمونیکی حول فاصله تعادلی پیوندی که از محاسبات تجربی ویا تئوری ناشی از ساختار الکترونی با استفاده از نرمافزارهای محاسباتی مانند روشهای ابتدا به ساکن مانند Gaussian به دست میآیند مدلسازی میشوند. برای بازتولید دقیق طیفهای ارتعاشی، میتوان از پتانسیل مورس با صرف محاسبات رایانهای استفاده کرد. عبارات زوایای دوسطحی یا پیچشی بهطور معمول دارای کمینههای مختلف هستند و بنابراین نمیتوانند به عنوان نوسانگر هارمونیک مدل شوند، اگرچه شکل تابعی خاص آنها با پیادهسازی متفاوت است. این کلاس از عبارات ممکن است شامل عبارات نامتناسب دوسطحی (دوهامنی) باشد، که بعنوان فاکتورهای تصحیح برای انحراف از سطح عمل میکنند (به عنوان مثال میتوان از آنها برای نگه داشتن مسطح حلقههای بنزن، یا اصلاح هندسه و کایرالی بودن اتمهای چهار ضلعی در نمایش اتم واحد استفاده کرد)
در کل عبارات غیر پیوندی هزینه محاسباتی بالایی دارند زیرا اگرچه برای یک اتم پیوند تنها با تعداد کمی از همسایگانش وجود دارد ولی روی تمام اتمهای موجود در ملکول برهمکنش دارند. خوشبختانه عبارت ون در والس به سرعت از بین میرود. این بهطور معمول با استفاده از یک پتانسیل ۶−۱۲ لنارد-جونز مدلسازی می شود، به این معنی که نیروهای جاذب با نسبت R − 6 و نیروهای دافع با نسبت r − 12 سقوط میکنند. در این پتانسیل r فاصله بین دو اتم است. قسمت دافع r − 12 با این حال غیر فیزیکی است، زیرا دافعه بصورت نمایی افزایش مییابد. توصیف نیروهای ون در والس توسط پتانسیل لنارد جونز ۶−۱۲ که در فواصل کوتاه نیز یه شکل قابل توجهی نادرست است.[1] بهطور کلی از شعاع قطع برای سرعت بخشیدن به محاسبه استفاده میشود به گونه ای که به جفت اتمهای با فاصله بیشتر از شعاع قطع، انرژی ون در والس صفر خواهند داشت.
محاسبه عبارات الکترواستاتیک بسیار دشوار است زیرا به سرعت با فاصله از بین نمیروند و فعل و انفعالات الکترواستاتیک با برد طولانی اغلب ویژگیهای مهم سیستم مورد مطالعه هستند (خصوصاً برای پروتئینها). شکل اساسی تابعی، پتانسیل کولوم است که فقط با نسبت r − 1 کاهش مییابد. روشهای مختلفی برای رفع این مشکل استفاده میشود که سادهترین آنها شعاع قطع مانند آن چیزی است که برای عبارت ون در والس استفاده میشود. با این حال، این یک ناپیوستگی شدید بین اتمهای داخل و اتمهای خارج از شعاع ایجادمیکند. تعویض یا مقیاس بندی تابعی که بروز انرژی الکترواستاتیک را مدل میکنند، روشهایی دقیق تر هستند که انرژی محاسبه شده را با ضریب تغییر مقادیر کاملاً متفاوت از ۰ تا ۱ در شعاع قطع خارجی و داخلی ضرب میکنند. سایر روشهای پیچیدهتر با محاسباتی سنگینتر مبتنی بر مش ذرات اوالد (PME) و الگوریتم چند قطبیهستند.
علاوه بر شکل تابعی هر عبارت انرژی، باید یک تابع انرژی مفید برای ثابت نیروها، ضرایب وان در والس و سایر عبارات ثابت اختصاص دهد. این عبارات، همراه با پیوندِ زاویه و مقادیر دوسطحی تعادلی، مقادیر بار جزئی، جرمها و شعاعهای اتمی و تعاریف تابع انرژی، در مجموع به عنوان یک میدان نیرو خوانده میشوند. پارامتر کردن معمولاً از طریق توافق با مقادیر تجربی و نتایج محاسبات نظری انجام میشود. میدان نیرو آلینگرز در آخرین نسخه MM4 برای گرمای تشکبل هیدروکربنها با خطای RMS معادل ۰٫۳۵ کیلو کالری در مول محاسبه میشود. طیفهای ارتعاشی با خطای RMS معادل ۲۴ cm-1، قیود چرخشی با خطای RMS معادل۲٫۲٪، طول پیوند C-C با ۰٫۰۰۰۴ درجه و زاویه C-C-C با۱ درجه خطا محسابه میشود[2]. نسخههای بعدی MM4 ترکیبات دارای ناهمگن مانند آمینهای آلیفاتیک را نیز پوشش میدهد[3]
هر میدان نیرو با ثوابت داخلی سازگار پارمتربندی میشود، اما معمولاً پارامترها از یک میدان نیرو به دیگری قابل انتقال نیستند.
موارد کاربرد
کاربرد اصلی مکانیک مولکولی در زمینه دینامیک مولکولی است که در آن از میدان نیرو برای محاسبه نیروهایی که روی هر ذره عمل میکنند و یک انتگرال مناسب برای مدلسازی دینامیک ذرات و پیشبینی مسیرهای واکنشها استفاده میشود. با توجه به نمونه برداری کافی و لر مبنای فرضیه ارگودیک، از خطوط سیر دینامیک مولکولی میتوان برای برآورد پارامترهای ترمودینامیکی یک سیستم یا کاوش خواص جنبشی مانند نرخ واکنش و مکانیسم استفاده کرد.
یکی دیگر از کاربردهای مکانیک مولکولی، کمینه سازی انرژی است که در نتیجه از میدان نیرو به عنوان معیار بهینهسازی استفاده میشود. در این روش از یک الگوریتم مناسب (به عنوان مثال گرادیان کاهشی) برای یافتن ساختار مولکولی در کمینههای موضعی انرژی استفاده میکند. این کمینهها مطابق با همصورتهای پایدار مولکول (در میدان نیروی انتخاب شده) هستند و حرکت مولکولی را میتوان به عنوان ارتعاشات در اطراف و برهمکنش بین این همصورتهای پایدار مدل کرد؛ بنابراین یافتن روشهای کمینه سازی انرژی موضعی همراه با بهینهسازی انرژی سراسری، یافتن کمینه انرژی سراسری (و سایرحالات کم انرژی) معمول است. در دمای محدود، مولکول بیشتر اوقات در این حالتهای کمینه انرژی قرار دارد، که در نتیجه بر خواص مولکولی اثر دارند. بهینهسازی سراسری(global optimization) میتواند با استفاده از الگوریتم تبرید شبیهسازی شده، الگوریتم متروپلیس-هیستینگز و سایر روشهای مونت کارلو یا استفاده از با روشهای تعیینی مختلف گسسته یا پیوسته برای بهینهسازی انجام شود. در حالی که میدان نیرو تنها مؤلفه آنتالپی در انرژی آزاد را نشان میدهد (و تنها این موئلفه در کمینهسازی انرژی دخیل است)، میتوان با استفاده از روشهای دیگر، مانند تجزیه و تحلیل حالت عادی، جزء آنتروپی را نیز بررسی کرد.
توابع انرژی پتانسل مکانیک مولکولی برای محاسبه ثابت پیوندی،[4][5][6][7][8] جنبششناسی خمشوندگی پروتئین،[9] تعادل پروتون دهی،[10] مختصات سایت فعال، استفاده شدهاست.[11] و برای طراحی پروتئین استفاده میشوند.[12]
محیط و حلالیت
در مکانیک مولکولی، روشهای مختلفی برای تعریف محیط پیرامون یک مولکول یا مولکولهای مورد علاقه وجود دارد. یک سیستم را میتوان در خلاء (شبیهسازی فاز گاز) بدون محیط اطراف شبیهسازی کرد، اما این معمولاً نامطلوب است زیرا اثر تصنعی در هندسه مولکولی، به ویژه در مولکولهای باردار وارد میکند. بارهای سطحی که معمولاً با مولکولهای حلال در برهمکنش قرار میگیرند، در عوض با یکدیگر برهمکنش میکنند و باعث تشکل ساختارهای مولکولی میشوند که ناممکن به نظر میرسند که اصلاً وجود داشته باشد. بهترین راه برای حل یک سیستم، قرار دادن مولکولهای ساده آب در جعبه شبیهسازی با مولکولهای مورد علاقه و تلقی مولکولهای آب به عنوان ذرات کنشگر مانند آنچه در این مولکولهای اصلی است، میباشد. انواع مدلهای آب با افزایش سطح پیچیدگی وجود دارد، آب را به عنوان یک کره سخت ساده (یک مدل اتم واحد)، به عنوان سه ذره جداگانه با زاویههای پیوندی ثابت، یا حتی به عنوان چهار یا پنج مرکز تعامل جداگانه ارائه میدهند تا الکترونهای جفت نشده را در اتم اکسیژن به محاسبه وارد کنند. هرچه مدلهای آب پیچیدهتر میشوند، شبیه سازیهای رایانهای مرتبط با محاسبات سنگینتر میشوند. یک روش برای کنارآمدن با این موضوع در حلال ضمنی پیدا شدهاست که جایگزین مولکولهای ساده آب شده و یک عبارت ریاضی برای بازتولیدی از رفتار میانگین مولکولهای آب (یا سایر حلالها مانند لیپیدها) را جایگزین میکند. این روش برای جلوگیری از اثر تصنعی ناشی از شبیهسازی خلاء مفید است و خواص توده (بالک) حلال را به خوبی تولید میکند، اما نمیتواند موقعیتهایی را تولید کند که مولکولهای آب فردی با آنها برهمکنش متفاوتی و بعضاً مطلوبی با مولکولهای مورد مطالعه داشته باشند.
بستههای نرمافزاری
این یک لیست محدود است؛ بستههای بسیاری دیگر در دسترس است.
- ACEMD - GPU MD[13]
- AMBER
- Ascalaph Designer[14]
- BOSS
- CHARMM
- COSMOS[15]
- سی پی ۲ کی
- CytoSolve[16]
- Ghemical
- گرومکس
- GROMOS
- HyperChem
- Internal Coordinate Mechanics (ICM)
- لمپس
- MacroModel
- MDynaMix
- Molecular Operating Environment (MOE)
- NAMD
- Q
- Q-Chem
- Spartan
- StruMM3D (STR3DI32)[17]
- Tinker
- X-PLOR
- Yasara
- Zodiac[18]
جستارهای وابسته
پیوند به بیرون
منابع
- Zgarbova M, et al. (2010). "Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations". Phys. Chem. Chem. Phys. 12 (35): 10476–10493. Bibcode:2010PCCP...1210476Z. doi:10.1039/C002656E. PMID 20603660.
- Allinger, N. L. ; Chen, K. ; Lii, J. -H. J. Comput. Chem. 1996, 17, 642 https://onlinelibrary.wiley.com/doi/abs/10.1002/(SICI)1096-987X(199604)17%3A5/6%3C642%3A%3AAID-JCC6%3E3.0.CO%3B2-U
- Kuo‐Hsiang Chen ,Jenn‐Huei Lii, Yi Fan, Norman L. Allinger J. Comput. Chem. 2007, 28, 2391 https://onlinelibrary.wiley.com/doi/full/10.1002/jcc.20737
- Kuhn B, Kollman PA (October 2000). "Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models". Journal of Medicinal Chemistry. 43 (20): 3786–91. doi:10.1021/jm000241h. PMID 11020294.
- Huo S, Massova I, Kollman PA (January 2002). "Computational alanine scanning of the 1:1 human growth hormone-receptor complex". J Comput Chem. 23 (1): 15–27. doi:10.1002/jcc.1153. PMID 11913381.
- Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA (August 2007). "Predicting absolute ligand binding free energies to a simple model site". J Mol Biol. 371 (4): 1118–34. doi:10.1016/j.jmb.2007.06.002. PMC 2104542. PMID 17599350.
- Wang J, Kang X, Kuntz ID, Kollman PA (April 2005). "Hierarchical database screenings for HIV-1 reverse transcriptase using a pharmacophore model, rigid docking, solvation docking, and MM-PB/SA". Journal of Medicinal Chemistry. 48 (7): 2432–44. doi:10.1021/jm049606e. PMID 15801834.
- Kollman PA, Massova I, Reyes C, et al. (December 2000). "Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models". Acc Chem Res. 33 (12): 889–97. CiteSeerX 10.1.1.469.844. doi:10.1021/ar000033j. PMID 11123888.
- Snow CD, Nguyen H, Pande VS, Gruebele M (November 2002). "Absolute comparison of simulated and experimental protein-folding dynamics". Nature. 420 (6911): 102–6. Bibcode:2002Natur.420..102S. doi:10.1038/nature01160. PMID 12422224.
- Barth P, Alber T, Harbury PB (March 2007). "Accurate, conformation-dependent predictions of solvent effects on protein ionization constants". Proc Natl Acad Sci USA. 104 (12): 4898–903. Bibcode:2007PNAS..104.4898B. doi:10.1073/pnas.0700188104. PMC 1829236. PMID 17360348.
- Chakrabarti R, Klibanov AM, Friesner RA (July 2005). "Computational prediction of native protein ligand-binding and enzyme active site sequences". Proc Natl Acad Sci USA. 102 (29): 10153–8. Bibcode:2005PNAS..10210153C. doi:10.1073/pnas.0504023102. PMC 1177389. PMID 15998733.
- Boas FE, Harbury PB (July 2008). "Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model". J Mol Biol. 380 (2): 415–24. doi:10.1016/j.jmb.2008.04.001. PMC 2569001. PMID 18514737.
- ACEMD - GPU MD
- Ascalaph
- COSMOS
- CytoSolve
- StruMM3D (STR3DI32)
- Zodiac بایگانیشده در ۲۰۰۹-۱۲-۱۶ توسط Wayback Machine