روش مونتکارلو
روش مونتکارلو (به انگلیسی: Monte Carlo method) (یا تجربه مونتکارلو) یک الگوریتم محاسباتی است که از نمونهگیری تصادفی برای محاسبه نتایج استفاده میکند. روشهای مونتکارلو معمولاً برای شبیهسازی سیستمهای فیزیکی، ریاضیاتی و اقتصادی استفاده میشوند.
| فیزیک محاسباتی |
|---|
 |
|
آنالیز عددی · شبیهسازی کامپیوتری |
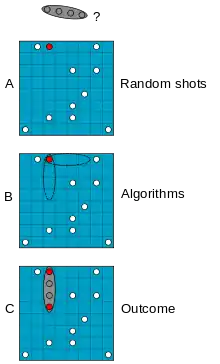
در علوم کامپیوتر روشی است که با پیمایش تمام فضای مسئله جواب را میابد.
از طرف دیگر روش مونتکارلو یک طبقه از الگوریتمهای محاسبه گر میباشند که برای محاسبه نتایج خود بر نمونه گیریهای تکرار شوندهٔ تصادفی اتکاء میکنند. روشهای مونتکارلو اغلب زمان انجام شبیهسازی یک سامانه ریاضیاتی یا فیزیکی استفاده میشوند. به دلیل اتکای آنها بر محاسبات تکراری و اعداد تصادفی یا تصادفی کاذب، روشهای مونتکارلو اغلب به گونهای تنظیم میشوند که توسط رایانه اجرا شوند. گرایش به استفاده از روشهای مونتکارلو زمانی بیشتر میشود که محاسبه پاسخ دقیق با کمک الگوریتمهای قطعی ناممکن یا ناموجه باشد.[1] روشهای شبیهسازی مونتکارلو مخصوصاً در مطالعه سیستمهایی که در آن تعداد زیادی متغیر با درجه آزادیهای دو به دو مرتبط وجود دارد مفید است، از جمله این سیستمها میتوان به سیالات، جامداتی که به شدت کوپل شدهاند، مواد بی نظم و ساختارهای سلولی (مدل سلولی پاتز – Potts- را ببیند) اشاره نمود. از آن گذشته، روشهای مونتکارلو برای شبیهسازی پدیدههایی که عدم قطعیت زیادی در ورودیهای آنها وجود دارد نیز مفید هستند، مثلاً محاسبه ریسک در تجارت. همچنین این روشها بهطور گستردهای در ریاضیات مورد استفاده قرار میگیرند: یک نمونه استفاده سنتی کاربرد این روشها در برآورد انتگرالهای معین است، به خصوص انتگرالهای چند بعدی با محدودههای مرزی پیچیده. واژه مونتکارلو در دهه ۱۹۴۰ (دهه ۱۳۱۰ شمسی) به وسیله فیزیکدانانی که روی پروژه ساخت یک سلاح اتمی در آزمایشگاه ملی لوس آلاموس آمریکا کار میکردند رایج شدهاست.[2]
تاریخچه
ریشه نام «مونتکارلو» از زبان ایتالیایی است و به اصلیت اسم شاهزاده کارلو سوم از موناکو بر میگردد که زیر نفوذ و حمایت دربار ایتالیا قرار داشت. تا قبل از سال ۱۸۶۱ که موناکو به شکلی خودمختار درآمد، زبان رسمی ایتالیایی بود، اما در یکصد سال گذشته، زبان رسمی به فرانسوی تغییر داده شد.[3]
مونتکارلو (در فرانسوی: Monte-Carlo) نام منطقهای است بسیار مشهور در کشور خودمختار موناکو واقع در اروپای غربی. جمعیت ساکن در مونتکارلو در حدود ۳۰۰۰ نفر را شامل میشود. منطقه مونتکارلو، ثروتمندترین منطقه از کشور خودمختار موناکو است.[4]
نام روش مونتکارلو توسط تحقیقات فیزیکدانانی چون استانیسلاو اولام، انریکو فرمی و جان فون نیومن شهرت فراوان یافت. این اسم مبدأیی به یک کازینو ای در موناکو است که عموی اولام برای قمار پول قرض میکردهاست. تصادفی بودن و تکرار طبیعی فرایندها مشابه فعالیتهای در کازینوها است.
کاربرد
روشهای تصادفی برای محاسبه و آزمایش (که عموماً به عنوان شبیهسازی تصادفی شناخته میشوند) را بدون تردید میتوان تا اولین پیشگامان نظریه احتمال دنبال کرد (سوزن بافون، کار جزیی روی نمونهها توسط ویلیام گوست)، ولی بهطور ویژه میتوان آن را در دوران قبل از محاسبات الکترونیکی دنبال کرد. تفاوت اساسی که معمولاً دربارهٔ روش شبیهسازی مونتکارلو بیان میشود این است که بهطور اصولی نوع روش شبیهسازی را وارون میکند و نظر مسایل را با یافتن مدل مشابه احتمالی به خود جلب میکند. روشهای پیشین برای شبیهسازی و مدلسازی آماری عموماً عکس این کار را انجام میدادند: استفاده از شبیهسازی برای امتحان کردن مسایل مشخص قطعی.
به هر حال همانطور که میدانیم مثالهای دیدگاه «وارون» به صورت تاریخی نیز وجود دارند، آنها تا قبل از آمدن روش مونتکارلو به عنوان یک روش عمومی در نظر گرفته نمیشدند.
شاید معروفترین استفادهٔ اخیر از این روش توسط انریکو فرمی در سال۱۹۳۰ باشد، هنگامی که او از یک روش تصادفی برای دستیابی به خواص نوترون تازه کشف شده، استفاده کرد. همچنین روشهای مونتکارلو مرکزیت شبیهسازی مورد نیاز در پروژهٔ منهتن را داشتند اگرچه که در آن زمان در استفاده از ابزارهای محاسباتی در محدودیت جدی قرار داشتند؛ بنابراین مونتکارلو در زمانی مورد مطالعه و بررسی توسط دانشمندان قرار گرفت که کامپیوترهای الکترونیکی برای اولین بار پا به عرصه گذاشتند. (از سال ۱۹۴۵ تا امروز)
در ۱۹۵۰ در لوس آلاموس برای تحقیقات جدیدی که دربارهٔ بمبهای هیدروژنی آغاز شده بود مورد استفاده قرار گرفت و در رشتههای فیزیک و شیمی فیزیک و تحقیق در عملیات مشهور شد.
شرکت رند(Rand) و نیروی هوایی ایالات متحده دو سازمان مرتبط برای جمعآوری و ارسال اطلاعات دربارهٔ روشهای مونتکارلو در طول این زمان بودهاست، و کاربردهای گستردهٔ این روش را یافتهاند.
استفاده از روش مونتکارلو نیاز به استفادهٔ مقادیر زیادی اعداد تصادفی دارد و این استفاده باعث کنار رفتن و عدم گسترش زایندههای اعداد شبه تصادفی بود. روش مونتکارلو را میتوان برای بسیاری از محاسبات مهندسی، مخصوصاً در بخش برق و تخمینهای آن استفاده نمود.
نگاه کلی
تنها یک روش مونتکارلو وجود ندارد، بلکه این واژه به گستره وسیعی از روشهایی که بسیار به کار گرفته میشوند اطلاق میگردد. به هر حال، این رویکردها از الگوی مشخصی پیروی میکنند:
- محدودهای از ورودیهای ممکن را تعریف میکنند.
- از آن محدوده ورودیهای تصادفی را تولید میکنند.
- با استفاده از ورودیهای بدست آمده یک سری محاسبات مشخص را انجام میدهند.
- نتایج هر یک از اجراهای محاسباتی را در پاسخ نهایی ادغام میکنند.
- مثال
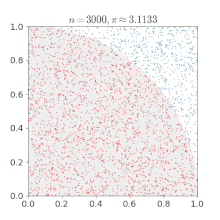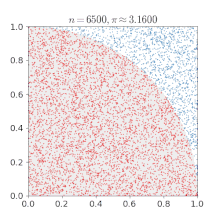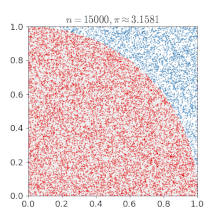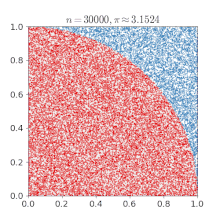
برای مثال میتوان مقدار عدد (پی) را با استفاده از روش مونتکارلو محاسبه نمود.
- یک مربع روی صفحه ترسیم کنید، سپس یک ربع دایره را درون آن محاط کنید. در ادامه چندین شکل با اندازه یکسان را روی آن بهطور یکنواخت پخش کنید (برای مثال، دانههای شن یا برنج) در سرتاسر مربع.
- سپس تعداد اشیاء درون دایره را بشمارید، در چهار ضرب کنید و عدد به دست آمده را بر تعداد کل اشیاء درون مربع تقسیم نمایید.
- نسبت اشیاء درون دایره در مقابل اشیاء درون مربع تقریباً برابر خواهد بود با ۴/π، که همان نسبت سطح دایرهاست به سطح مربع؛ بنابراین شما تخمینی از عدد π را به دست آوردهاید. توجه داشته باشید که چگونه تخمین عدد π از یک الگوی مشخص شده در روش مونتکارلو پیروی میکند.
ابتدا ما یک محدوده از متغیرها را تعریف کردیم که یک مربع بود که دایره ما را احاطه کرده بود. سپس ورودیها را بهطور تصادفی تولید کردیم (پخش دانهها بهطور یکنواخت درون مربع)، سپس محاسبات را برای هر ورودی انجام دادیم (بررسی کردیم که آیا دانه درون دایره هست یا نه). در آخر، تمام جوابها را در جواب نهایی ادغام نمودیم. همچنین به این نکته توجه داشته باشید که دو ویژگی مشترک دیگر روشهای مونتکارلو این است:
- اتکای محاسبات بر اعداد تصادفی خوب
- همگرایی تدریجی به سمت تخمینهای بهتر در زمانی که دادههای بیشتری شبیهسازی میشوند.
کاربردها
شبیهسازی مونتکارلو بهطور ویژهای در مطالعهٔ سیستمها با درجه آزادی زوج متعدد مورد استفاده قرار میگیرد مثل مایعات، مواد متخلخل، مایعات شدیداً زوج و ساختارهای حفره دار (مانند ساختار حفره دار پات). روشهای مونتکارلو به صورت وسیعی در مدلسازی پدیدهها با مقادیر قابل توجهی عدم اطمینان در ورودیها مورد استفاده قرار میگیرد مثل:
محاسبهٔ ریسک در تجارت (نمونه کاربرد آن در اقتصاد، مدلسازی تصادفی است) استفادهٔ کلاسیک از این روشها برای ارزیابی و محاسبهٔ انتگرالهای معین، بهطور خاص برای انتگرالهای چند بعدی باشد با شرایط مرزی پیچیده، استفاده میشود.
روشهای مونتکارلو همچنین برای محاسبهٔ ارزش سرمایه شرکتها، ارزیابی سرمایهٔ پروژهها نیز استفاده میشود.
همچنین روشهای مونتکارلو در فیزیک محاسباتی، شیمی فیزیک و زمینههای مرتبط با این دو کاربرد فراوان دارد.
مونتکارلو علاوه بر این، تحت تأثیر بسزای خود را در حل معادله دیفرانسیلهای زوج انتگرالی در زمینهٔ تشعشع و انتقال انرژی ثابت کردهاست پس بنابراین این روش برای آشکارسازی جهانی محاسبات که مدلهای مجازی سه بعدی تصاویر فوتوریالیستیک را تولید میکند، مورد استفاده قرار میگیرد.
روشهای مونتکارلو در زمینههای بسیاری نیز در ریاضیات محاسباتی مورد استفاده قرار میگیرد، که فقط یک خوش شانس میتواند نتیجهٔ صحیح بگیرد. یک مثال کلاسیک، الگوریتم رابین است که برای آزمایش اول بودن اعداد مورد استفاده قرار میگیرد.
همچنین الگوریتم لاس وگاس نیز به همین موضوع میپردازد ولی با ایدهای متفاوت.
زمینههای کاربرد مونتکارلو
- گرافیک، بهطور خاص خط اثر پرتو
- مدلسازی جا به جایی نور در رشتههای بیولوژیک
- مونتکارلو در اقتصاد
- مهندسی اطمینان
- در شبیهسازی پیچش برای پیشبینی ساختار پروتین
- در تحقیقات تجهیزات نیم رسانا، برای مدلسازی جا به جایی حاملهای کنونی
- در محیط زیست، بررسی آلایندهها
- کاربرد مونتکارلو در فیزیک استاتیک
- در طراحی احتمالاتی برای شبیهسازی و درک تغییرپذیری
- در شیمی فیزیک، بهطور خاص برای شبیهسازی قالبهای اتمهای درگیر
- در علوم کامپیوتر:
- الگوریتم لاس وگاس
- LURCH
- Computer Go
- بازیها
- کاربردهای گسترده در فیزیک هستهای
ریاضیات
کاربرد روش مونتکارلو در ریاضیات و آمار بسیار گستردهاست. با استفاده از این روش، با انتخاب تصادفی یک یا تعداد محدودی پاسخ از میان پاسخهای موجود، تلاش میشود تا به راه حل قابل قبولی دست یافت. این تکنیک زمانی ارزش پیدا میکند، که مجموعه آلترناتیوهای موجود برای پاسخ یک مسئله بسیار بزرگ باشد و عملاً امکان آزمودن تمامی آنها وجود نداشته باشد؛ یک نمونه کلاسیک در این زمینه، الگوریتم رابین برای تست اول بودن یک عدد میباشد. الگوریتم رابین بیان میدارد که با داشتن یک عدد مانند n که غیر اول است، یک عدد تصادفی مانند x، دارای احتمال ۷۵٪ است تا ثابت کند عدد n عددی غیر اول است؛ بنابراین، با داشتن عدد غیر اولی مانند n اگر عددی تصادفی مانند x یافت شود، بهطوریکه ثابت کند n احتمالاً عددی اول است، ما موفق به آزمودن گزینههایی شدهایم که احتمال رخداد آنها ۱ به ۴ است. حال با یافتن ۱۰ عدد دیگر مانند x که ثابت کند n احتمالاً عددی اول است، موفق به یافتن مجموعهای شدهایم که احتمال وقوع آنها ۱ به میلیون است. الگوریتم لاس وگاس نیز از روش مونتکارلو بهره میبرد. یکی از رایجترین کاربرد مونتکارلو، انتگرال گیری مونتکارلو است.
انتگرالگیری
روشهای قطعی انتگرالگیری عددی به وسیله دریافت عدد نمونههای فاصله دار یکنواخت از یک تابع است. بهطور کلی، این روش برای توابع یک متغیری بسیار خوب جواب میدهد. در حالی که برای تابعی از بردارها، روشهای تربیع قطعی بی تأثیراند. ه (مثلاً برای محاسبهٔ انتگرال 2X اعداد تصادفی تولید شده توسط توابع گاوس را در صفحهای مشخص میریزد و با استفاده از نسبت نقاط داخل و خارج تابع مساحت محاسبه میشود)
برای انتگرالگیری عددی از یک تابع دو متغیره از بردارها، نقاط فاصله دار به صورت چهارخانه بهطور مساوی روی صفحه دو بعدی مورد نیاز است.
برای نمونه یک صفحهٔ ۱۰x۱۰ نیاز به ۱۰۰ نقطه دارد. اگر بردار ما ۱۰۰ بعدی باشد، تقسیمبندی مورد نیاز روی صفحه، نیاز به
(عدد گوگول) نقطه دارد که برای محاسبه بسیار بزرگ است.
روش مونتکارلو روشی را برای خروج از این رشد نمایی پیشنهاد میکند. تا زمانی که تابع مورد سؤال یک تابع خوش رفتار است، به وسیله انتخاب تصادفی نقاط در فضای ۱۰۰ بعدی و گرفتن نوعی میانگین از مقادیر تابع در این نقاط، میتواند تخمین زده شود. با به کارگیری قانون اعداد بزرگ، این روش همگرایی به را نشان میدهد.
روشهای انتگرالگیری
- مدل نمونه برداری مستقیم
- نمونه برداری با اهمیت
- نمونه برداری طبقه به طبقه
- نمونه برداری طبقه به طبقهٔ بازگشتی
- الگوریتم وگاس
- راه تصادفی مونتکارلو شامل زنجیرهای مارکوو
- الگوریتم متروپولیس-هاستینگ
- مدلسازی گیبس
فیزیک
یکی از مهمترین کاربردهای روش مونتکارلو در زمینههای فیزیک محاسباتی، شیمیفیزیک و کرومودینامیک کوانتومی جهت انجام محاسبات پیچیده مربوط به ساخت پوشش گرمایی مورد استفاده بر روی یک فضاپیما یا موشک بالستیک میباشد.
شیمی
همچنین از کاربردهای عملی این روش در دانش شیمیفیزیک، میتوان به ساخت و بررسی مدل مولکولی اشاره نمود که به عنوان جایگزینی برای روش محاسباتی دینامیک مولکولی و شیمی کوانتومی مطرح میشود.
هدف اصلی روش مونتکارلو یا دینامیک مولکولی محاسبه خواص تعادلی یک سیستم است. در این روش پس از حصول اطمینان از بودن در حالت تعادل، با تغییر تصادفی موقعیت و جهتگیری ذرات موجود در سیستم، پیکربندیهایی از سیستم تولید میشود. منظور از پیکربندی مجموعهای از موقعیت و جهتگیری همهٔ ذرات در یک حالت از تمام حالتهای ممکن سیستم است. پیکربندی تولید شده در هر مرحله با احتمالی که توسط قوانین ترمودینامیک آماری تعیین میگردد، رد یا تأیید میشود. این احتمال به انرژی پتانسیل بین دو ذره بستگی دارد. در هر پیکربندی خاصیت ترمودینامیکی مورد نظر اندازهگیری میشود. با نمونه برداری صحیح از این پیکربندیها و میانگین گیری، میتوان مقدار آن خاصیت را در حال تعادل به دست آورد.[5]
مزیت این روش به دینامیک مولکولی، نیاز نداشتن به محاسبهٔ اندازه حرکت برای هر ذرهاست که باعث کاهش زمان محاسبات رایانهای میشود. از معایب این روش میتوان به دست نیاوردن اطلاعات راجع به دینامیک سیستم اشاره کرد.
اقتصاد
یکی از مهمترین کاربردهای روش مونتکارلو، حل معادله موسوم به بلک-شولز در مورد مدلسازی بازار سهام دارای نرخهای تصادفی است. حل این معادله منجر به ساخت یک مدل شبیهسازی شده اقتصادی میگردد. این مدل اقتصادی برای پیشبینی تغییرات در یک بازار بورس مورد استفاده قرار میگیرد.
جستارهای وابسته
منابع
- مشارکتکنندگان ویکیپدیا. «Monte_Carlo_simulation». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۶ مارس ۲۰۰۸.
- Douglas Hubbard «How to Measure Anything: Finding the Value of Intangibles in Business» pg. 46, John Wiley & Sons, 2007
- [The beginning of the Monte Carlo method http://library.lanl.gov/la-pubs/00326866.pdf]
- About the Principality of Monaco, The Official website of the Principality of Monaco
- Monaco (12/08)
- شبیهسازیهای رایانهای، سیفالله جلیلی شابک ۹۷۸−۹۶۴−۸۷۰۳−۳۹−۹
- Arnaud Doucet, Nando de Freitas and Neil Gordon, Sequential Monte Carlo methods in practice, 2001, ISBN 0-387-95146-6.
- P. Kevin MacKeown, Stochastic Simulation in Physics, 1997, ISBN 981-3083-26-3
- Harvey Gould & Jan Tobochnik, An Introduction to Computer Simulation Methods, Part ۲، Applications to Physical Systems, 1988, ISBN 0-201-16504-X
- C.P. Robert and G. Casella. «Monte Carlo Statistical Methods» (second edition). New York: Springer-Verlag, 2004, ISBN 0-387-21239-6
- R.Y. Rubinstein and D.P. Kroese (۲۰۰۷). «Simulation and the Monte Carlo Method» (second edition). New York: John Wiley & Sons, ISBN 978-0-470-17793-8.
- Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller and Edward Teller, «Equation of State Calculations by Fast Computing Machines» , Journal of Chemical Physics, volume ۲۱، p. ۱۰۸۷ (۱۹۵۳) (doi:۱۰٫۱۰۶۳/۱٫۱۶۹۹۱۱۴)
- N. Metropolis and S. Ulam, «The Monte Carlo Method» , Journal of the American Statistical Association, volume ۴۴، number ۲۴۷، pp. ۳۳۵–۳۴۱ (۱۹۴۹) (doi:۱۰٫۲۳۰۷/۲۲۸۰۲۳۲)
- Fishman, G.S. , (1995) Monte Carlo: Concepts, Algorithms, and Applications, Springer Verlag, New York.
- Judgement under Uncertainty: Heuristics and Biases, ed. D. Kahneman and A. Tversky,(Cambridge University Press, ۱۹۸۲)
- R. E. Caflisch, Monte Carlo and quasi-Monte Carlo methods, Acta Numerica vol. ۷، Cambridge University Press, ۱۹۹۸، pp. 1–49.