کما (موسیقی)

در تئوری موسیقی یک کُما [پ 1] یا کاما [پ 2] (به انگلیسی: comma) فاصله‌ای کوچک در زیرایی یک نت است که حاصل تفاوت ناشی از کوک کردن آن نت از دو راه متفاوت است.[en 1] دو نوع کما در تئوری موسیقی به طور متداول مورد بحث قرار می‌گیرد: کمای متداول (به انگلیسی: common comma) یا کمای همصدا، و دیگری کمای بیشینه (به انگلیسی: comma maxima) که به آن کمای فیثاغورثی هم می‌گویند.[en 1] وقتی واژهٔ «کما» بدون هیچ پسوندی استفاده شود، غالباً منظور همان «کمای همصدا» است.[en 2]

دو نت مترادف در یک دستگاه کوک می‌توانند صداهایی با تفاوت اندک نسبت به هم داشته باشند؛ این تفاوت صدا به طور کلی یک «کما» نامیده می‌شود. برای نمونه، در کوک پنج حدی نت لا بملی که به اندازهٔ یک فاصلهٔ سوم بزرگ پایین‌تر از نت دوی پنجم (C5) کوک بشود، و نت سل دیز که به اندازهٔ دو فاصلهٔ سوم بزرگ بالاتر از دوی چهارم (C4) کوک شده، صدایی متفاوت خواهند داشت (یکی اندکی زیرتر و دیگری اندکی بمتر). تفاوت نت‌های یادشده در کوک پنج حدی، تقریباً ۴۰٪ یک نیم‌پرده است و برای شنونده به آسانی قابل تشخیص خواهد بود.

به طور متداول، کماها به صورت فواصلی بین دو نیم‌پرده تعریف می‌شوند. هر کدام از روش‌های کوکی که مبتنی بر اعتدال میانگین هستند یک گام کروماتیک تولید می‌کنند که در آن دو نوع نیم‌پرده وجود دارد (نیم‌پردهٔ دیاتونیک و نیم‌پردهٔ کروماتیک)، و اختلاف این دو یک کما است که با نام دیز کوچک شناخته می‌شود. به طور مشابه، روش‌های کوک‌کردنی که بر کوک فیثاغورثی مبتنی هستند هم دو نوع نیم‌پرده (دیاتونیک و کروماتیک) تولید می‌کنند و اختلاف این دو همان کمای فیثاغورثی است.

دیز کوچک، تعریف شده با استفاده از روش کوک یک‌چهارم کمای میانگین. فاصلهٔ بین میان‌پردهٔ دیاتونیک (m2) و میان‌پردهٔ کروماتیک (A1) همان فاصلهٔ بین دو نت مترادف (در اینجا «دو دیز» و «ر بمل») است. صدای هر چهار نتی که نمایش داده شده (دو، دو دیز، ر بمل، ر) در این روش با هم متفاوت و برای گوش انسان قابل تمییز است.

بشنوید

کمای فیثاغورثی (که با نماد PC نمایش داده شده) فاصلهٔ بین دو نت مترادف «دو دیز» و «ر بمل» است که با روش فیثاغورثی کوک شده‌اند. همچنان که از مقایسهٔ دو تصویر نمایان است، فاصلهٔ بین نت‌های «دو» و «ر» در کوک فیثاغورثی بیشتر از روش یک‌چهارم کمای میانگین است. در مقابل، اندازهٔ کمای فیثاغورثی اندکی کوچکتر از کمای همصدا است.

در نظام کوک خالص، بیشتر از دو نوع نیم‌پرده می‌تواند ساخته شود. در نتیجه یک روش کوک‌کردن می‌تواند با کماهای متعددی شناخته شود. برای نمونه در یکی از روش‌های جدیدتر کوک پنج حدی، چهار نوع نیم‌پرده و چهار کمای مختلف تولید می‌شود.

در اعتدال مساوی، فاصله‌ها بر اساس کسرهای سادهٔ ریاضی تعریف نمی‌شوند و دو نت مترادف دقیقاً یک صدا خواهند داشت. در نتیجه در این روش کوک کردن، عملاً کما وجود ندارد.

اندازه‌گیری

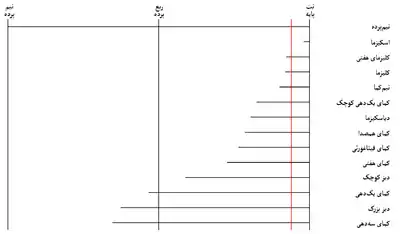
مقایسهٔ اندازهٔ کماهای مختلف بر حسب سنت. ربع پرده و نیم‌پردهٔ نمایش داده شده، بر اساس اعتدال مساوی هستند. خط قرمزرنگ حداقلی از تفاوت بسامد را که برای گوش انسان قابل تشخیص است نشان می‌دهد.

اندازهٔ کما معمولاً در واحد «سِنت» گزارش و مقایسه می‌شود (هر سنت یک هزار و دویستم یک اکتاو است در مقیاس لگاریتمی؛ از آنجا که هر اکتاو شامل دوازده نیم‌پرده است، پس هر نیم‌پرده صد سنت دارد). با این حال تعریف اندازهٔ کما می‌تواند در مقایسه با کماهای دیگر (به خصوص کمای فیثاغورثی و کمای همصدا) نیز انجام گیرد.

در جدول زیر، m2 به فاصلهٔ دوم کوچک (نیم‌پردهٔ دیاتونیک) اشاره می کند و A1 به همصدای افزوده (نیم‌پردهٔ کروماتیک)، و S₁ و S₂ و S₃ . S₄ معرف نیم‌پرده‌هایی هستند که به روش کوک پنج حدی تعریف شده باشند. در ستون‌های «فاصلهٔ اول» و «فاصلهٔ دوم»، فرض شده که فاصله‌ها با استفاده از نظام کوک خالص به دست آمده‌اند. دست آخر این که از کمای فیثاغورثی (PC) و کمای همصدا (SC) به عنوان خط‌کشی برای اندازه‌گیری دیگر کماها استفاده شده‌است. برای نمونه تفاوت بین کمای فیثاغورثی و کمای همصدا برابر با یک اسکیزما است. این تفاوت در بیشتر موارد برای گوش انسان قابل تشخیص نیست.

به جز آنچه در جدول زیر آمده، کماهای دیگر هم تعریف شده‌اند.[en 3]

نام کما	دیگر نام‌ها	تعاریف				اندازه
		بر اساس تفاوت بین نیم‌پرده‌ها	بر اساس کماها	بر اساس فاصله‌ها		سنت	نسبت
		بر اساس تفاوت بین نیم‌پرده‌ها	بر اساس کماها	فاصله ۱	فاصله ۲	سنت	نسبت
اسکیزما		A1 منهای m2 در کوک یک‌دوازدهم کمای میانگین	یک PC منهای یک SC	۸ پنجم درست + یک سوم بزرگ	۵ اکتاو	۱٫۹۵	۳۲٬۸۰۵:۳۲٬۷۶۸
کلیزمای هفتی				۳ سوم بزرگ	یک اکتاو منهای یک کمای هفتی	۷٫۷۱	۲۲۵:۲۲۴
کلیزما				۶ سوم کوچک	یک تریتاو (یک اکتاو + یک پنجم درست)	۸٫۱۱	۱۵٬۶۲۵:۱۵٬۵۵۲
کمای یک‌دهی کوچک[en 4]				۱ دوم خنثی	یک دوم بزرگ	۱۷٫۴۰	۱۰۰:۹۹
دیاسکیزما		m2 منهای A1 در کوک یک‌ششم کمای میانگین، S₃ منهای S₂ در کوک پنج حدی	دو SC منهای یک PC	۳ اکتاو	۴ پنجم درست + ۲ سوم بزرگ	۱۹٫۵۵	۲٬۰۴۸:۲٬۰۲۵
کمای همصدا (SC)	کمای دیدیموس (به انگلیسی: Didymus)	S₂ منهای S₁ در کوک پنج حدی		۴ پنجم درست	۲ اکتاو + ۱ سوم بزرگ	۲۱٫۵۱	۸۱:۸۰
کمای همصدا (SC)	کمای دیدیموس (به انگلیسی: Didymus)	S₂ منهای S₁ در کوک پنج حدی		دوم بزرگ	دوم بزرگ	۲۱٫۵۱	۸۱:۸۰
کمای فیثاغورثی (PC)	کمای دایتونیک (به انگلیسی: ditonic)	A1 منهای m2 در کوک فیثاغورثی		۱۲ پنجم درست	۷ اکتاو	۲۳٫۴۶	۵۳۱٬۴۴۱:۵۲۴٬۲۸۸
کمای هفتی[en 5]	کمای آرکیتاس (به انگلیسی: Archytas)			هفتم کوچک	هفتم کوچک هفتی	۲۷٫۲۶	۶۴:۶۳
دیز کوچک		m2 منهای A1 در کوک یک‌چهارم کمای میانگین S₃ منهای S₁ in 5-limit tuning	سه SC منهای یک PC	اکتاو	۳ سوم بزرگ	۴۱٫۰۶	۱۲۸:۱۲۵
کمای یک‌دهی[en 6][en 7]	ربع پرده یک‌دهی			سه‌پرده یک‌دهی	چهارم درست	۵۳٫۲۷	۳۳:۳۲
دیز بزرگ		m2 منهای A1 در کوک یک‌سوم کمای میانگین S₄ منهای S₁ در کوک پنج حدی	چهار SC منهای یک PC	۴ سوم کوچک	اکتاو	۶۲٫۵۷	۶۴۸:۶۲۵
کمای سه‌دهی				سه‌پردهٔ سه‌دهی	چهارم درست	۶۵٫۳۴	۲۷:۲۶

اهمیت تاریخی

کمای همصدا نقشی حیاتی در تاریخ موسیقی داشته‌است. این کما میزان تغییری است که در کوک فیثاغورثی باید داده شود تا فواصل سوم کوچک یا سوم بزرگ خالص تولید شوند. در کوک فیثاغورثی، تنها صداهای هماهنگ عبارت بودند از فاصلهٔ پنجم درست و نقیض آن یعنی چهارم درست. در این کوک، فاصلهٔ سوم بزرگ (با نسبت ۸۱:۶۴) و سوم کوچک (با نسبت ۳۲:۲۷) ناهماهنگ هستند، و به همین خاطر نوازندگان نمی‌توانستند آزادانه از آن‌ها در آکوردها استفاده کنند، لذا آهنگسازان مجبور می‌شدند که از بافت ساده‌تری در آثارشان استفاده کنند.

در اواخر قرون وسطی، نوازندگان پی بردند که با دستکاری خفیفی در زیر و بمی برخی نت ها می‌توانند فواصل سوم فیثاغورثی را تبدیل به فواصلی هماهنگ بکنند. برای مثال اگر بسامد نت «می» به اندازهٔ یک کمای همصدا (نسبت ۸۱:۸۰) کاهش داده شود، ترکیب «دو-می» (سوم بزرگ) و «می-سل» (سوم کوچک) خالص می‌شود. به طور دقیق‌تر فاصلهٔ «دو-می» بر اساس نسبت محاسبه شده در پایین، کمی بمتر می‌شود:

{81 \over 64}\times {80 \over 81}={{1\times 5} \over {4\times 1}}={5 \over 4}

و در همین حال، فاصلهٔ «می-سل» به اندازهٔ نسبت محاسبه شده در پایین، کمی زیرتر می‌شود:

{32 \over 27}\times {81 \over 80}={{2\times 3} \over {1\times 5}}={6 \over 5}

این اتفاق باعث ایجاد روش‌های جدیدی برای کوک کردن سازها شد (از جمله کوک یک‌چهارم کمای میانگین) که اجازه می‌داد که موسیقی با بافت پیچیده‌تری توسعه یابد. به طور خاص این تحولات راه را برای چندصدایی و ملودی‌های دارای همراه‌نوازی فراهم کرد. از آن زمان روش‌های بیشتری برای کوک کردن ایجاد شده اما کمای همصدا به عنوان یک عدد مرجع برای اندازه‌گیری میزان دستکاری زیرایی نت‌ها در این کوک‌ها به کار گرفته می‌شود.

تعاریف جایگزین

در آن روش‌های کوک مبتنی بر اعتدال میانگین که فاصلهٔ پنجم درست را کوچکتر از ۷۰۰ سنت تعریف می‌کنند، کمای همصدا در اصل یک دوم کاسته است و می‌تواند به شکل‌های زیر نیز تعریف گردد.

دوم کوچک و همنوای افزوده (یا همان نیم‌پرده‌های دیاتونیک و کروماتیک)، یا
دوم بزرگ و کاسته سوم، یا
سوم کوچک و دوم افزوده، یا
سوم بزرگ و چهارم کاسته، یا
چهارم درست و سوم افزوده، یا
چهارم افزوده و پنجم کاسته، یا
پنجم درست و ششم کاسته، یا
ششم کوچک و پنجم افزوده، یا
ششم بزرگ و هفتم کاسته، یا
هفتم کوچک و ششم افزوده، یا
هفتم بزرگ و هنگام کاسته.

در کوک فیثاغورثی و سایر روش‌های کوک مبتنی بر اعتدال میانگین که فاصلهٔ پنجم درست را کوچکتر از ۷۰۰ سنت تعریف می‌کنند، کاما نقیض یک فاصلهٔ دوم کاسته است، و لذا نقیض فواصل بالا می‌باشد. به طور دقیق‌تر، در این روش‌های کوک فاصلهٔ دوم کاسته یک فاصلهٔ پایین‌رونده است و کاما نقیض بالاروندهٔ آن است. برای مثال، کامای فیثاغورثی (با نسبت ۵۳۱٬۴۴۱:۵۲۴٬۲۸۸ یا حدود ۲۳٪۳ سنت) را می‌توان بر اساس تفاوت بین یک نیم‌پردهٔ دیاتونیک و نیم‌پردهٔ کروماتیک محاسبه کرد، که نقیض فاصلهٔ دوم کاسته است (که نسبت ۵۲۴٬۲۸۸:۵۳۱٬۴۴۱ یا حدود -۲۳٫۵ سنت دارد).

در هر یک از روش‌های کوک که بالاتر گفته شد، تمام فاصله‌هایی که فهرست شده‌اند با هم برابر هستند. برای مثال در کوک فیثاغورثی این فواصل همگی برابر با نقیض یک کامای فیثاغورثی هستند و در کوک یک‌چهارم کمای میانگین، همگی برابر با یک دیز کوچک هستند.

کما در موسیقی دارای ریزپرده

در موسیقی دارای ریزپرده (نظیر موسیقی سنتی ایرانی و موسیقی ترکی) از کما برای تعریف اندازهٔ ریزپرده‌هایی نظیر سری و کرن استفاده می‌شود.

فرهاد فخرالدینی در کتاب «تجزیه و تحلیل و شرح ردیف موسیقی ایران» کما را یک نهم پرده تعریف می‌کند و می‌نویسد که نیم‌پردهٔ کروماتیک چهار کما و نیم‌پردهٔ دیاتونیک پنج کما است.[1] از آنجا که هر پرده ۲۰۰ سنت است، این یعنی کما برابر $200/9\approx 22.22\ cent$ تعریف شده‌است. این نسبت، کمی بیشتر از کمای همصدا و کمی کمتر از کمای فیثاغورثی است و با هر دو ناسازگار است. این تعریف از کما، با کمای هلدری مطابقت دارد؛ در موسیقی ترکی هم این کما (گاهی با نام «کمای عربی») مطرح شده‌است.

فخرالدینی همچنین می‌نویسد که محل قرارگیری پرده‌های سازهای اساتید مختلف موسیقی سنتی ایرانی با هم متفاوت بوده‌است و برخی فواصل بر حسب این که بالارونده نواخته می‌شوند یا پایین‌رونده، متفاوت کوک می‌شده‌اند.[2]

نت‌نویسی

از آنجا که کما تفاوت بسیار اندکی در بسامد صداست که بسیار کوچک‌تر از آن است که به خودی خود در نواختن موسیقی به کار گرفته بشود، در نت‌نویسی رایج معمولاً علامت کما استفاده نمی‌شود. برخی متخصصین تئوری موسیقی از علامت «+» برای نمایش کمای همصدا استفاده می‌کنند و برای کمای فیثاغورثی ترکیبی از علامت‌های تغییر نواک (نظیر دیز یا بمل) و چندین علامت «+» را به کار می‌برند.

نمایش کمای همصدا برای نت «دو»
نمایش کمای فیثاغورثی برای نت «دو»

پانویس

در آثار فارسی املای «کما» رایج‌تر است. برای مثال، تجزیه و تحلیل و شرح ردیف موسیقی ایران، فرهاد فخرالدینی، انتشارات معین، ۱۳۹۴.
املای فارسی comma در معنای دیگرش (ویرگول) به صورت «کاما» است. املای «کما» در فارسی در معنای دیگرش (از هوش رفتن)، مربوط به واژهٔ coma در انگلیسی است که تنها یک m دارد. تلفظ comma با دو m در زبان‌های لاتین مثل انگلیسی و فرانسوی، (چه به معنای ویرگول، چه در موسیقی) یکسان است؛ با این حال، در متون فارسی املای «کما» برای comma به مفهوم موسیقایی، رایج‌تر است.

منابع

منابع فارسی

فخرالدینی، فرهاد (۱۳۹۴). تجزیه و تحلیل و شرح ردیف موسیقی ایران. تهران: نشر معین. ص. ص ۳۸. شابک ۹۷۸-۹۶۴-۱۶۵-۰۹۸-۰. پارامتر |تاریخ بازیابی= نیاز به وارد کردن |پیوند= دارد (کمک)
فخرالدینی، فرهاد (۱۳۹۴). تجزیه و تحلیل و شرح ردیف موسیقی ایران. تهران: نشر معین. ص. ص ‍۱۸. شابک ۹۷۸-۹۶۴-۱۶۵-۰۹۸-۰. کاراکتر zero width joiner character در |صفحه= در موقعیت 3 (کمک); پارامتر |تاریخ بازیابی= نیاز به وارد کردن |پیوند= دارد (کمک)

منابع انگلیسی

Grove, George (1879). Dictionary of Music and Musicians. MacMilland and Co. p. 880.
Benson, Dave (2006). Music: A Mathematical Offering. Cambridge University Press. p. 171. ISBN 0-521-85387-7.
"List of commas, by prime limit". Xenharmonic wiki. Archived from the original on 9 February 2017. Retrieved 2016-12-30.
Haluška, Ján (2003). The Mathematical Theory of Tone Systems, p.xxvi. ISBN 0-8247-4714-3.
David Dunn, 2000. Harry Partch: an anthology of critical perspectives.
Rasch, Rudolph (2000). "A Word or Two on the Tunings of Harry Partch", Harry Partch: An Anthology of Critical Perspectives , p.34. Dunn, David, ed. ISBN 90-5755-065-2. Difference between 11-limit and 3-limit intervals.
Rasch, Rudolph (1988). "Farey Systems of Musical Intonation", Listening 2, p.40. Benitez, J.M. et al., eds. ISBN 3-7186-4846-6. Source for 32:33 as difference between 11:16 & 2:3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] در آثار فارسی املای «کما» رایج‌تر است. برای مثال، تجزیه و تحلیل و شرح ردیف موسیقی ایران، فرهاد فخرالدینی، انتشارات معین، ۱۳۹۴.

[2] املای فارسی comma در معنای دیگرش (ویرگول) به صورت «کاما» است. املای «کما» در فارسی در معنای دیگرش (از هوش رفتن)، مربوط به واژهٔ coma در انگلیسی است که تنها یک m دارد. تلفظ comma با دو m در زبان‌های لاتین مثل انگلیسی و فرانسوی، (چه به معنای ویرگول، چه در موسیقی) یکسان است؛ با این حال، در متون فارسی املای «کما» برای comma به مفهوم موسیقایی، رایج‌تر است.

[10] فخرالدینی، فرهاد (۱۳۹۴). تجزیه و تحلیل و شرح ردیف موسیقی ایران. تهران: نشر معین. ص. ص ۳۸. شابک ۹۷۸-۹۶۴-۱۶۵-۰۹۸-۰. پارامتر |تاریخ بازیابی= نیاز به وارد کردن |پیوند= دارد (کمک)

[11] فخرالدینی، فرهاد (۱۳۹۴). تجزیه و تحلیل و شرح ردیف موسیقی ایران. تهران: نشر معین. ص. ص ‍۱۸. شابک ۹۷۸-۹۶۴-۱۶۵-۰۹۸-۰. کاراکتر zero width joiner character در |صفحه= در موقعیت 3 (کمک); پارامتر |تاریخ بازیابی= نیاز به وارد کردن |پیوند= دارد (کمک)

[grove-3] Grove, George (1879). Dictionary of Music and Musicians. MacMilland and Co. p. 880.

[4] Benson, Dave (2006). Music: A Mathematical Offering. Cambridge University Press. p. 171. ISBN 0-521-85387-7.

[5] "List of commas, by prime limit". Xenharmonic wiki. Archived from the original on 9 February 2017. Retrieved 2016-12-30.

[6] Haluška, Ján (2003). The Mathematical Theory of Tone Systems, p.xxvi. ISBN 0-8247-4714-3.

[7] David Dunn, 2000. Harry Partch: an anthology of critical perspectives.

[Rasch-8] Rasch, Rudolph (2000). "A Word or Two on the Tunings of Harry Partch", Harry Partch: An Anthology of Critical Perspectives , p.34. Dunn, David, ed. ISBN 90-5755-065-2. Difference between 11-limit and 3-limit intervals.

[9] Rasch, Rudolph (1988). "Farey Systems of Musical Intonation", Listening 2, p.40. Benitez, J.M. et al., eds. ISBN 3-7186-4846-6. Source for 32:33 as difference between 11:16 & 2:3.