گراف وتری

در ریاضیات، حوزهٔ نظریهٔ گرافها، گراف وتری گرافی است که هر دور به طول چهار یا بیشتر از آن شامل وتر باشد. (وتر: یالی است که دو رأس از دور که در دور شرکت نکرده باشند را به هم وصل می‌کند). به عبارت دیگر، هر دور القایی در گراف می‌بایست حداکثر سه رأس داشته باشد. گراف‌های وتری زیرمجموعه‌ای از گراف‌های آرمانی می‌باشند که در مدت زمانی چندجمله‌ای شناسایی می‌شوند. اگر ورودی مسایلی همچون رنگ‌آمیزی گراف، گرافی وتری باشد در مدت زمانی چندجمله‌ای حل می‌شوند.

یک دور (سیاه) با دو وتر (سبز). حذف یک یال سبز گراف را به گرافی غیر وتری تبدیل می‌کند زیرا یال سبز دیگر با سه یال سیاه، تشکیل دوری به طول چهار و بدون وتر می‌دهد.

طرد آرمانی و شناسایی بهینه

${\displaystyle \{v_{1},v_{2},...,v_{n}\}}$ یک ترتیب طرد آرمانی(به انگلیسی: perfect elimination ordering) از رئوس گراف است به طوری‌که به ازای هر راس ${\displaystyle v_{i}}$، زیرگراف القایی ناشی از رئوس ${\displaystyle v_{i}}$ وهمسایه‌های آن در زیرگراف القایی ناشی از ${\displaystyle {v_{1},v_{2},...,v_{i}}}$ گرافی کامل باشد. Rose, Lueker & Tarjan (1976) نشان دادند که یک ترتیب طرد آرمانی از گرافی وتری را می‌توان به‌طور بهینه با الگوریتمی به نام lexicographic breadth-first search پیدا کرد.

خوشه‌های فرین و رنگ‌آمیزی گراف

کاربرد دیگر ترتیب طرد آرمانی پیدا کردن خوشهٔ فرین در یک گراف وتری در مدت زمانی چندجمله‌ای است، در حالی‌که این مسئله در حالت کلی از مسائل NP-complete است. در حالت کلی یک گراف وتری تعدادی خطی خوشهٔ فرین دارد در حالی‌که این تعداد در گراف‌های دیگر می‌تواند نمایی باشد. برای بدست آوردن خوشه‌های فرین از گراف وتری، ابتدا یک ترتیب طرد آرمانی (در صورت وجود) پیدا می‌کنیم. سپس از ابتدای این ترتیب شروع کرده و به ازای هر رأس ${\displaystyle v_{i}}$ زیرگراف القایی ناشی از این رأس و رئوس قبلی آن در ترتیب را (که تشکیل خوشه می‌دهند) را در نظر می‌گیریم. خوشهٔ با اندازهٔ بیشینه در میان این خوشه‌ها، خوشهٔ فرین خواهد بود. از آنجا که گراف وتری آرمانی است، اندازهٔ خوشهٔ فرین، همان عدد رنگی گراف خواهد بود. گراف‌های وتری، ترتیب پذیر آرمانی هستند: با اعمال رنگ‌آمیزی حریصانه بر روی ترتیب معکوس طرد آرمانی می‌توان به‌طور بهینه آن را رنگ کرد.

جداساز مینیمال

جداساز رأسی در هر گراف، مجموعه‌ای از رئوس است که با حذف آن‌ها گراف ناهمبند می‌شود. جداساز مینیمال است اگر هیچ زیرمجموعهٔ محضی از آن این ویژگی را نداشته باشد. برطبق قضیهٔ Dirac (1961) در گراف‌های وتری، هر جداساز مینیمال یک خوشه است. Dirac با این ویژگی آرمانی بودن گراف‌های وتری را اثبات کرد. گراف‌های وتری به‌طور استقرایی توسط گراف‌هایی تعریف می‌شوند که رئوس آن‌ها به سه زیرمجموعهٔ ناتهی ${\displaystyle A,B,S}$ افراز شوند، به طوری‌که ${\displaystyle A\cup S}$ و ${\displaystyle B\cup S}$ هردو تشکیل یک زیرگراف القایی وتری دهند، ${\displaystyle S}$ خوشه باشد و هیچ یالی بین ${\displaystyle A}$ و ${\displaystyle B}$ نباشد.

گراف تقاطع زیردرخت‌ها

گرافی وتری با هشت رأس و گراف تقاطع حاصل از هشت زیردرخت آن .

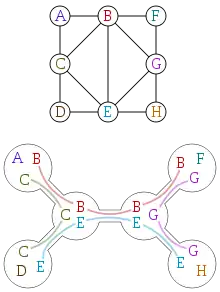
ویژگی دیگر گراف‌های وتری مربوط به درخت و زیردرخت‌ها است. Gavril (1974) در یک درخت گراف تقاطع آن این گونه ساخته می‌شود: به ازای هر زیر درخت آن یک رأس در نظر می‌گیریم. دو رأس از این گراف مجاورند اگر زیردرخت متناظر آن‌ها در حداقل یک رأس مشترک باشند. Gavril (1974) نشان داد که این گراف، گرافی وتری است. نمایش گراف وتری به صورت تقاطع زیردرخت‌ها، یک درخت تفکیک با پهنا درخت یکی کمتر از بزرگترین خوشهٔ گراف بدست می‌دهد. درخت تفکیک هر گراف را می‌توان به صورت نمایش زیرگرافی از گراف وتری در نظر گرفت. درخت تفکیک، همان درخت اتصال در الگوریتم درخت اتصال است.

مکمل وتری و پهنا درخت

مکمل وتری گراف دلخواه ${\displaystyle G}$، گرافی وتری است که ${\displaystyle G}$ زیرگراف آن باشد. اگر ${\displaystyle H}$ مکمل وتری گراف ${\displaystyle G}$ با عدد خوشه‌ای (تعداد رئوس خوشهٔ بیشینه گراف) کمینه باشد، در آن صورت پهنادرخت ${\displaystyle G}$ یکی کمتر از عدد خوشه‌ای ${\displaystyle H}$ است. k-درخت گرافی است که افزودن یک یال به آن، پهنادرخت آن را بزرگتر از k می‌کند. بنابراین k-درخت مکمل وتری خودش است و رده‌ای از گراف‌های وتری را تشکیل می‌دهد.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Chordal Graph». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۰ آذر ۱۳۹۲.