گنبد (هندسه)
در هندسه ، گنبد جسمي است که با اتصال دو چند ضلعی ، كه یکی (قاعده) دو برابر بیشتر از ديگرى ضلع دارد ، توسط یک باند متناوب از مثلث هاي متساوی الساقین و مستطیل ها ، تشکیل می شود. اگر مثلث ها ،متساوی الاضلاع و مستطیل ها ،مربع باشند و قاعده و وجه مقابل آن چند ضلعی هاي منتظم باشند ،آنگاه گنبد های مثلثی(J3) ، مربعی(J4) و پنجضلعی(J5) همه در میان اجسام جانسون شمرده می شوند و می توانند به ترتيب با زدن مقاطع به مکعبهشتوجهی، لوزمکعبهشتوجهی و لوزبیستدوازدهوجهی به دست آيند.
 گنبد پنجضلعی (مثال) | |
| نماد اشلفلی | | t{n} |
| وجوه | n مثلث, n مربع, ١ n-ضلعي, ١ ٢n-ضلعي |
| اضلاع | ٥n |
| رئوس | ٣n |
| گروه تقارن | Cnv, [1,n], (*nn), order 2n |
| گروه چرخشي | Cn, [1,n]+, (nn), order n |
| مزدوج | ? |
| ويژگى ها | محدب |
یک گنبد را می توان منشوری دید که در آن تعداد اضلاع یکی از قاعده ها با ادغام رأس های مجاور نصف شده است.
مي توان به يك گنبد نماد گسترش داده شده شلفي {n} || t{n} را داد،يك چندضلعى منتظم{n} و بريده شده اش {t{n يا {2n}.
گنبد ها از انواع منشوروار ها هستند.
مزدوج آنها شامل شکلی است که به نوعی جوشکاری بین نیمی از پاد دوهرم n پهلو و هرم 2n پهلو است.
مثال ها
| n | ٢ | ٣ | ٤ | ٥ | ٦ |
|---|---|---|---|---|---|
| Name | {٢} || t{2} | {٣} || t{٣} | {٤} || t{٤} | {٥} || t{٥} | {٦} || t{٦} |
| گنبد |  گنبد دو ضلعي |
 گنبد مثلثی |
 گنبد مربعی |
 گنبد پنجضلعی |
 گنبد ششضلعی (صاف) |
| چندوجهى مرتبط | منشور سه پهلو |
مکعبهشتوجهی |
لوزمکعبهشتوجهی |
لوزبیستدوازدهوجهی |
Rhombitrihexagonal tiling |
سه چندوجهی كه بالا ذكر شد تنها گنبدهای محدب و داراى وجوه منتظم هستند: "گنبد شش ضلعی" یک صفحه است و "منشور مثلثی" را می توان گنبد درجه ٢ در نظر گرفت (گنبد یک قطعه خط و یک مربع). با این حال ، ممکن است گنبد های درجه بالاتر با مثلث هاى غير متساوي الأضلاع و مستطيل ها ساخته شوند.
گنبد هاي ستارهای
| n / d | ٤ | ٥ | ٧ | ٨ |
|---|---|---|---|---|
| ٣ |  گنبد مربعی ستارهای{٤/٣} |
 گنبد پنجضلعی ستارهای{٥/٣} |
 گنبد هفتضلعی{٧/٣} |
 گنبد هشتضلعی{٨/٣} |
| ٥ | — | — |  گنبد هفتضلعی ستارهای{٧/٥} |
 گنبد هشتضلعی ستارهای{٨/٥} |
| n⁄d | ٣ | ٥ | ٧ |
|---|---|---|---|
| ٢ |  نیمه گنبد مثلثی ستارهای |
 نیمه گنبد پنجضلعی |
 نیمه گنبد هفتضلعی |
| ٤ | — | 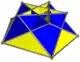 نیمه گنبد پنجضلعی ستارهای |
 نیمه گنبد هفتضلعی ستارهای |
گنبد های ستارهای برای هر پایه {nd} که در آن ٦> {nd}>٦٥ و d فرد است. در اين محدوده ها ، گنبدها به شکل صفحه فرو می ریزند: فراتر از حد بالا، مثلث ها و مربع ها دیگر نمی توانند فاصله بین دو چند ضلعی را پوشش دهند. وقتی d زوج است ، پایه پایین {nd٢} دوباره ساخته مي شود كه می توان با برداشتن این وجه و در عوض اجازه دادن به مثلث ها و مربع ها كه در آن به هم متصل شوند، یک نیمه گنبد (به انگلیسی: cuploid) ایجاد كرد.هرگاه در نيمه گنبديnd از ٢ بزرگتر باشد مثلث ها و مربع ها نمي توانند كل قاعده را بپوشانند و بخشى از آن خالي مي ماند مانند {٥/٢} و {٧/٢} كه اگر از بالا مشاهده شوند فاضى خالي دارند اما {٥/٤} و {٧/٤} ندارند.
در هر گنبد يا نيمه گنبد nd با ارتفاع h همواره است و اگر nd برابر با ٦ يا ٦٥ باشد ٠=h و اگر nd برابر ٢ باشد، h حداكثر است (منشور سه پهلو كه مثلث ها عموديند).
پاد گنبد
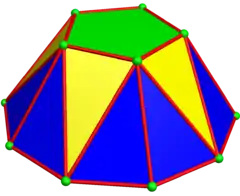 نمونه پنج ضلعي | |
| نماد اشلفلی | | t{n |
| وجوه | ٣n مثلث ١ n-ضلعي, ١ ٢n-ضلعي |
| اضلاع | ٦n |
| رئوس | ٣n |
| گروه تقارن | Cnv, [1,n], (*nn), order 2n |
| گروه چرخشي | Cn, [1,n]+, (nn), order n |
| مزدوج | ? |
| ويژگى ها | محدب |
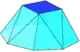
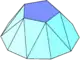
یک پاد گنبد n-ضلعى از یک قاعده منتظم ٢n-ضلعي ،٣n مثلث شامل دو نوع و وجه بالايى n-ضلعى منتظم ساخته شده است. اگر n برابر با ٢ باشد، وجه بالايى به یک لبه کاهش می یابد. رئوس چند ضلعی بالا با راس در چند ضلعی پایین هم راستا ميشود.
پاد گنبد را نمی توان به گونه اى ساخت كه همه وجوهش منظم باشند ، اگرچه بعضی از آنها را می توان با اضلاع برابر ساخت. اگر n-ضلعى و مثلث های بالا منظم باشند ، پایه 2n-ضلعى نمی تواند مسطح و منتظم باشد.چرا كه در چنین حالتی ، n = 6 یک شش ضلعی منظم و مثلث متساوی الاضلاع یک کاشی كاري شش ضلعی شل(به انگلیسی: snub hexagonal tiling) ايجاد می کند ، که می تواند در یک چند ضلعی حجم صفر بسته شود و پایه آن یک 12 ضلعى متقارن به شکل یک شش ضلعی بزرگتر ميباشد ، چرا كه دارای جفت های مجاور از اضلاع همخط است.
با وصل كردن دو گنبد از قواعدشان يك دوپاد گنبد (به انگلیسی: bianticupola) ايجاد مى شود.
| n | ٢ | ٣ | ٤ | ٥ | ٦... |
|---|---|---|---|---|---|
| نام | s{2} || t{2} | s{3} || t{3} | s{4} || t{4} | s{5} || t{5} | s{6} || t{6} |
| تصوير |  دوضلعی |
 مثلثی |
 مربعی |
 پنجضلعی |
 ششضلعی |
| نما | 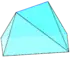 |
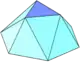 |
 |
 |
|
| گسترده |  |
ابرگنبد
ابرگنبد یا گنبد چندوجهی یک خانواده از چهاربعدى هاى محدب ، مشابه با گنبد است. پایه های هر یک جسم افلاطونی و گسترش آن است.
| نام | گنبد چهاروجهی | گنبد مکعبی | گنبد هشتوجهی | گنبد دوازدهوجهی | گنبد کاشیکاری ششضلعی | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| نماد اشلفلی | {3,3} || rr{3,3} | {4,3} || rr{4,3} | {3,4} || rr{3,4} | {5,3} || rr{5,3} | {6,3} || rr{6,3} | |||||
| Segmentochora index |
K4.23 | K4.71 | K4.107 | K4.152 | ||||||
| شعاع كره محيطي(به انگلیسی: circumradius) | 1 | sqrt((3+sqrt(2))/2) = 1.485634 |
sqrt(2+sqrt(2)) = 1.847759 |
3+sqrt(5) = 5.236068 |
||||||
| تصوير |  |
 |
 |
 |
||||||
| خانه هاى داخلي و بيروني(به انگلیسی: Cap cells) |   |
  |
  |
  |
  | |||||
| رئوس | ١٦ | ٣٢ | ٣٠ | ٨٠ | ∞ | |||||
| اضلاع | ٤٢ | ٨٤ | ٨٤ | ٢١٠ | ∞ | |||||
| وجوه | ٤٢ | {٣} ٢٤ + {٤} ١٨ | ٨٠ | {٣} ٣٢ + {٤} ٤٨ | ٨٢ | {٣} ٤٠ + {٤} ٤٢ | ١٩٤ | {٣} ٨٠ + {٤} ٩٠+ {٥} ٢٤ | ∞ | |
| خانه ها | ١٦ | ١ چهاروجهی ٤ منشور مثلثی ٦ منشور مثلثی ٤ هرم مثلث القاعده ١ مکعبهشتوجهی |
٢٨ | ١ مکعب ٦ منشور مربعی ١٢ منشور مثلثیs ٨ هرم مثلث القاعده ١ لوزمکعبهشتوجهی |
٢٨ | ١ هشتوجهی ٨ منشور مثلثی ١٢ منشور مثلثی ٦ هرم مربعالقاعده ١ لوزمکعبهشتوجهی |
٦٤ | ١ دوازدهوجهی ١٢ منشور پنجضلعی ٣٠ منشور مثلثی ٢٠ هرم مثلث القاعده ١ |
∞ | ١ کاشیکاری ششضلعی ∞ منشور ششضلعی ∞ منشور مثلثی ∞ هرم مثلث القاعده ١ rhombitrihexagonal tiling |
منابع
- ویکیپدیا انگلیسی