آرایه پویا


آرایه پویا، در علوم کامپیوتر، آرایه‌ای است که می‌تواند تغییر اندازه دهد و اجازه دهد عناصری به آن اضافه یا از آن حذف شود. امروزه امکان انجام این عمل در بسیاری از کتابخانه‌های استاندارد زبان‌های رایج برنامه‌نویسی تعبیه شده‌است. در یک آرایه پویا در ابتدای کار حافظه اختصاص داده نمی‌شود؛ به‌طوری‌که اندازه‌اش غیرقابل تغییر باشد.

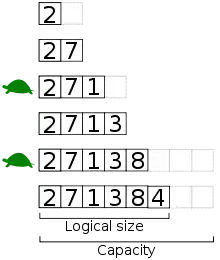
شکل بالا اضافه کردن چندین مقدار را به یک آرایه پویا نمایش می دهد. خانه های خاکستری برای گسترش رزرو شده اند. اکثر عملیات ها سریع هستند (زمان ثابت) اما آن هایی که با لاکپشت نمایش داده شده اند به اندازه ضریبی از اندازه آرایه زمان می برند.

آرایه‌های پویای کراندار و ظرفیت آن‌ها

ساده‌ترین آرایه پویا با اختصاص دادن آرایه‌ای به طول ثابت ساخته می‌شود که بعد آن را به دو قسمت تقسیم می‌کنند: قسمت اول عناصر آرایه پویا را ذخیره می‌کند و قسمت دوم ذخیره شده، یا بدون استفاده می‌ماند. سپس می‌توان با استفاده از فضای رزرو شده در زمانی ثابت عناصر را به انتهای آرایه پویا اضافه کرد یا آن‌ها را حذف کرد، تا زمانی که این فضا به‌طور کامل استفاده شود. تعداد عناصری که توسط محتویات آرایه پویا استفاده می‌شود اندازه منطقی یا اندازه آن است، در حالیکه اندازه آرایه زیرین ظرفیت آرایه پویا نام دارد، که حداکثر اندازه منطقی ممکن است. در برنامه‌هایی که اندازه منطقی کراندار است، این ساختار داده کفایت می‌کند. تغییر دادن اندازه آرایه زیرین عملی هزینه بر است، گاهی ناچار می‌شویم تمام محتویات آرایه را کپی کنیم.

تصاعد هندسی و هزینه واگذار شده

برای جلوگیری از تحمیل هزینه‌های اضافی حاصل از تغییر اندازه دادن‌های مکرر، آرایه‌های پویا به مقدار زیادی تغییر اندازه می‌دهند، مثلاً به دو برابر اندازه اولیه تغییر اندازه می‌دهند، و فضای رزرو شده را برای بسط بعدی استفاده می‌کنند. عمل اضافه کردن یک عنصر باید مانند زیر انجام شود:

function insertEnd(dynarray a, element e)
 if (a.size = a.capacity)
 // (اندازه را به دو برابر مقدار اولیه تغییر می‌دهیم):
 a.capacity ← a.capacity * 2
 // (کپی کردن محتویات در محل حافظه جدید)
 a[a.size] ← e
 a.size ← a.size + 1

در فرایند درج n عنصر، ظرفیت‌ها تشکیل تصاعد هندسی می‌دهند. بسط دادن آرایه با هر نسبت ثابتی تضمین می‌کند وارد کردن عصر در کل از (O(n زمان می‌برد، یعنی وارد کردن هر عنصر زمان سرشکن شده ثابتی می‌برد. مقدار این تناسب منجر به لزوم سبک‌سنگین کردن این فصله زمانی می‌شود: زمان متوسط هر بار وارد کردن تقریباً (a/(a-۱ است، در حالی که تعداد خانه‌های تلف شده از بالا به a−۱)n) کراندار است. انتخاب a بستگی به برنامه دارد، ولی معمولاً a=۲ می‌گیرند. بعلاوه در بسیاری از آرایه‌های پویا اگر مقدار استفاده شده از حدی کمتر شود، مانند ۳۰٪ ظرفیت، آن را آزاد می‌کنند. آرایه‌های پویا مثال رایجی در تدریس تحلیل سرشکن شده[1] هستند.

کارایی
Linked
list		ArrayDynamic
array
Indexing Θ(n) Θ(1) Θ(1)
Insertion/deletion at end Θ(1) N/A Θ(1)
Insertion/deletion in middle Θ(1) N/A Θ(n)
Wasted space (average) Θ(n) 0 Θ(n)

کارایی آرایه پویا شبیه آرایه‌است، بعلاوه عمل حذف و افزودن عناصر به انتها:

  • گرفتن یا قرار دادن مقدار در محلی خاص (زمان ثابت)
  • به ترتیب روی عناصر حرکت کردن (زمان خطی)
  • وارد کردن یا پاک کردن عنصر در وسط آرایه (زمان خطی)
  • وارد کردن یا پاک کردن عنصر در آخر آرایه (زمان ثابت سرشکن)

بسیاری از مزیت‌های آرایه‌ها در آرایه‌های پویا نیز وجود دارد، از جمله محل مناسب مرجع و استفاده از حافظه نهان، تراکم (کم استفاده کردن از حافظه)، و دسترسی تصادفی. معمولاً آرایه‌های پویا در کل فقط یک حافظه اضافی کوچکی برای اطلاعات اندازه و ظرفیت دارند. این ویژگی موجب می‌شود آرایه‌های پویا ابزار مناسبی برای ساختن داده ساختار متناسب با حافظه نهان شوند. آرایه‌های پویا در مقایسه با لینک لیست، قابلیت شاخص گذاری[2] سریع تری دارند (زمان ثابت در برابر زمان خطی) و معمولاً به دلیل اصلاح محل مرجع عناصر سریعتر می‌توان بر روی عناصر واقع در خانه‌های آرایه حرکت کرد؛ اگرچه، آرایه‌های پویا برای وارد کردن در محلی دلخواه یا پاک کردن از جایگاهی اختیاری زمانی خطی نیاز دارند، چون همه عناصر بعدی باید یک عنصر جابه‌جا شوند، در حالیکه لینک لیست می‌تواند این عمل را در زمانی ثابت انجام دهد. به وسیلهٔ میانگیر وقفه[3] و متغیرهای بردار صف شده این اشکال را برطرف کرده‌اند که در مورد آن در قسمت متغیرها بحث شده‌است. همچنین، ممکن است یافتن فضایی پیوسته در ناحیه یک حافظه بسیار قطعه بندی شده هزینه بر یا غیرممکن باشد، در حالیکه لینک لیست‌ها نیازی ندارند همه داده ساختار به‌طورپیوسته در حافظه ذخیره شود.

متغیرها

میانگیرهای وقفه شبیه آرایه‌های پویا هستند ولی اجازه می‌دهند عملگرهای کارای درج و حذف نزدیک محل اختیاری مشابه جمع شوند. برخی از پیاده‌سازی‌های صف دو سر از آرایه‌های صف دو سر استفاده می‌کنند، که اجازه درج/جابجایی در هر دو سر، به جای یک طرف می‌دهد. Goodrich الگوریتمی از آرایه‌های پویا به نام Tiered Vectors ارائه کرد که کارایی آن برای درج و حذف از وسط آرایه با حفظ ترتیب n۱/۲ O(است. درخت آرایه‌ای درهم[4] یک الگوریتم آرایهٔ پویا است که توسط Sitarski در سال ۱۹۹۶ ساخته شده‌است. درخت آرایه‌ای درهم حافظه‌ای از مرتبه n۱/۲ هدر می‌دهد، که n تعداد عناصر آرایه‌است. وقتی دنباله‌ای از اشیا به انتهای درخت آرایه‌ای درهم می‌افزاییم، کارکرد سرشکن الگوریتم O(۱) است. در سال ۱۹۹۹ Brodnik et al. در مقاله‌ای یک داده ساختار آرایه پویای صفی[5] توصیف کرد، که در هر نقطه‌ای از زمان تنها n۱/۲ فضا برای n عنصر هدر می‌داد، و آن‌ها کران پایینی را ثابت کردند که نشان می‌داد در هر آرایه پویایی اگر عملگرها می‌خواهند زمان ثابت سرشکنی بگیرند حداقل به این مقدار فضا نیاز هست. بعلاوه، برای مواردی که رشد کردن و جمع شدن میانگیرنه تنها درحالت سرشکن بلکه در بدترین حالت ثابت باشد، متغیری ارائه کردند. در سال ۲۰۰۲ Bagwell الگوریتم Vlist را ارائه کرد، که می‌تواند برای پیاده‌سازی آرایه پویا اقتباس شود.

زبان‌های پشتیبانی‌کننده

در C++, Std::vector یک نمونه پیاده‌سازی برای آرایه‌های پویا است، همان‌طور که کلاس‌های ArrayList توسط API java و.NET Framework عرضه شده‌است. کلاس نوعی[6] List<> نیز توسط version 2.0 of the.NET Framework عرضه شده، پیاده‌سازی دیگری برای آرایه‌های پویا است. Delphiو Dآرایه‌های پویا را در هسته زبان پیاده‌سازی کرده‌اند. بسیاری از زبان‌های مستند[7] مانند Perl و PHP پیشنهاد می‌دهند آرایه‌های پویا جزو ساختمان و به عنوان گنه داده‌های اولیه در نظر گرفته شوند.

منابع

Wikipedia contributors, "Dynamic array," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Dynamic_array&oldid=290138184 (accessed May 15, 2009).

پانویس
  1. amortized analysis
  2. indexing
  3. gap buffer
  4. Hash Array Tree
  5. tiered dynamic array
  6. generic
  7. scripting languages
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.