درخت سرخ-سیاه
در علم رایانه، ساختمان داده درخت قرمز-سیاه بلوک، یک نوع درخت جستجوی دودویی خود-متوازن است. این ساختمان داده را ابتدا رودولف بایر در سال ۱۹۷۲ با نام «درخت دودویی B متقارن» ابداع کرد ولی نام جدید آن از پایاننامهٔ لیو.جی.گیباس و رابرت سجویک گرفته شدهاست. این ساختمان داده بسیار پیچیده است با این حال اعمال مربوط به آن حتی در بدترین حالت نیز زمان اجرای خوبی دارند، در واقع زمان جستجو، حذف، و درج برای این درخت مانند درخت AVL لگاریتمی است ( که تعداد گرههای موجود در درخت است). مزیت عمده این ساختمان داده نسبت به درخت AVL این است که اعمال درج و حذف با تنها یک بار پیمایش درخت از بالا به پایین و تغییر رنگ گرهها انجام میشوند و در نتیجه پیادهسازی این درخت از درخت AVL سادهتر است.
| درخت سرخ-سیاه | ||
|---|---|---|
| نوع | درخت | |
| سال اختراع شدن | ۱۹۷۲ | |
| اختراع شده توسط | رودلف بابر | |
| پیچیدگی زمانی بر حسب نماد اوی بزرگ | ||
| میانگین | بدترین حالت | |
| فضا | O(n) | O(n) |
| جستجو | O(log n) | O(log n) |
| درج | O(log n) | O(log n) |
| حذف | O(log n) | O(log n) |
ویژگیها
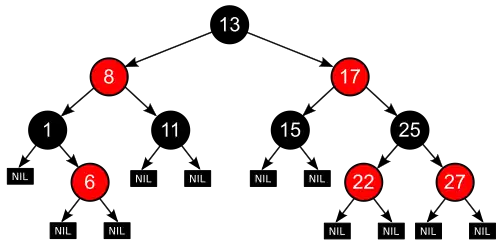
درخت قرمز-سیاه یک درخت جستجوی دودویی است که ویژگیهای زیر را دارد:
- هر گره با یکی از دو رنگ سیاه یا قرمز رنگ آمیزی میشود.
- ریشه همیشه به رنگ سیاه است.
- اگر گرهای قرمز باشد فرزندان آن باید سیاه باشند.
- تمامی مسیرها از یک گره به برگها (گرههای null) باید دارای تعداد مساوی گره سیاه باشند.
- تمامی برگها سیاه هستند. (برگ گرهای است که فرزندی نداشته باشد- همان گرههای null)
ویژگیهای بالا موجب این خصوصیت مهم درختهای قرمز-سیاه میشوند:
- اگر یک درخت قرمز سیاه n گره غیر null داشته باشد ارتفاع درخت حداکثر خواهد بود.
ویژگی فوق باعث میشود تا درختهای قرمز-سیاه کارایی مناسبی در اعمال جستجو، درج، و حذف داشته باشند.
همچنین به خاطر این که در تمام مسیرهای از ریشه به برگ، تعداد گرههای سیاه برابر است (ویژگی ۴) و ممکن نیست دو گره قرمز پشت سر هم قرار بگیرند (ویژگی ۳)، در این نوع درختها طول بلندترین مسیر از ریشه تا برگ هیچ وقت بزرگتر از دو برابر طول کوتاهترین مسیر ریشه تا برگ نمیشود.
با توجه به ویژگیهای بالا درختهای قرمز-سیاه (بر خلاف درختهای جستجوی دودویی معمولی) هیچ وقت دچار عدم توازن شدید نمیشوند و زمان اجرای لگاریتمی اعمال در این درختها تضمین شدهاست.
شباهت به درختهای بی مرتبه ۴
.svg.png.webp)
یک درخت قرمز-سیاه ار نظر ساختار شبیه یک درخت بی مرتبه ۴ است که در آن هر گره میتواند ۱ تا ۳ مقدار و همچنین ۲ تا ۴ اشاره گر به فرزندانش داشته باشد. در هر درخت بی، هر گره تنها یک مقدار دارد که برابر مقدار گره سیاه در درخت قرمز-سیاه است، و یک مقدار دلخواه دارد که و/یا بعد از آن در همان گره آمدهاست، که هر دوی آنها مساوی گره قرمز در درخت قرمز-سیاه هستند. یک راه دیدن این برابری این است که در گرههای قرمز درخت قرمز-سیاه در یک نمایش گرافیکی به سمت بالا حرکت کنیم، بهطوریکه با پدر سیاهشان در یک ردیف قرار بگیرند و یک دسته افقی را تشکیل دهند. در درخت بی، یا در نمایش گرافیکی تغییر یافته درخت قرمز-سیاه که گفته شد، همه برگها عمق یکسانی دارند. در این حالت درخت قرمز-سیاه، از نظر ساختار با درخت بی مرتبه ۴ برابر است که حداقل میزان پرشدن در یک دسته برابر ۳۳٪ است. این نوع درخت بی، عمومی تر از درخت قرمز-سیاه است اما هنگام تبدیل به درخت قرمز-سیاه، ابهاماتی دارد چون از یک درخت بی مرتبه ۴، چندین درخت قرمز-سیاه ساخته میشود. اگر یک دسته در درخت بی تنها ۱ مقدار را شامل شود، این مقدار کمینه است، گره مربوطه سیاه است و دو اشاره گر به فرزندانش دارد. اگر یک دسته شامل ۳ مقدار شود، مقدار وسطی در یک گره سیاه قرار میگیرد و گرههای کناری آن باید قرمز باشند. اگر دسته شامل ۲ مقدار باشد، هر کدام از آنها میتواند در درخت قرمز-سیاه، سیاه باشد و دیگری باید قرمز باشد؛ بنابراین درخت بی مرتبه ۴، مشخص نمیکند که کدامیک از مقادیر در هر دسته ریشه سیاه کل آن دسته و پدر بقیه مقادیر دسته است. با وجود این، عملیات در درختهای قرمز-سیاه از نظر زمان بهینه تر هستند چون نیازی به نگهداشتن برداری از مقادیر نیست. این نگهداری زمانی که مقادیر مستقیماً در هر گره ذخیره شدهاند، نسبت به وقتی که تنها مرجع آنها نگهداری شدهاست، پر هزینه است. البته گرههای درخت بی از نظر حافظه به صرفه تر هستند چون لازم نیست برای آنها صفت رنگ نگهداری شود. در عوض باید مشخص شود کدام بخش از دسته استفاده شدهاست. میتوان شباهتهایی با درختهای بی مرتبههای بالاتری که از نظر ساختار شبیه درخت دودویی رنگ شده باشند هم ایجاد کرد چون تنها به رنگهای بیشتری نیاز است. مثلاً فرض کنید آبی را هم استفاده کنیم. در نتیجه درخت آبی-قرمز-سیاه مثل درخت قرمز-سیاه تعریف میشود اما با این محدودیت اضافه که دو گره متوالی از نظر مقدار نباید آبی باشند و همه گرههای آبی باید فرزندان گره قرمز باشند. چنین درختی معادل یک درخت بی میشود که دستههای آن حداکثر ۷ مقدار و با این رنگها دارند :آبی، قرمز، آبی، سیاه، آبی، قرمز، آبی (هر گروه حداکثر ۱ گره سیاه، ۲ گره قرمز و ۴ گره آبی دارد). برای تعدیل کردن حجم مقادیر، درج و حذف در یک درخت دودویی سریعتر از درختهای بی است چون درختهای رنگ شده تلاشی برای بیشینه کردن مقدار پر شدن در یک دسته افقی از گرهها نمیکنند. (تنها کمینه مقدار پرشدن در درختهای دودویی رنگ شده تضمین شدهاست). چرخش در درختهای بی سریع تر است (چون چرخشها اغلب در دسته یکسان رخ میدهند به جای اینکه در چند گره مجزا در یک درخت دودویی رنگ شده انجام شوند). با این وجود برای مرتبسازی حجم زیادی از دادهها، درختهای بی بسیار سریعتر هستند چون با گروهی کردن چند فرزند در یک دسته و امکان دسترسی محلی، فشرده تر شدهاند. همه بهینهسازیهای ممکن در درختهای بی برای افزایش متوسط میزان پرشدن گروهها در درختهای دودویی رنگ شده هم ممکن است. بیشینه کردن میزان پرشدن در یک درخت بی، مانند کم کردن ارتفاع درخت چند رنگ است که با افزایش تعداد گرههای غیر سیاه انجام میشود. بدترین حالت زمانی رخ میدهد که همه گرهها در یک درخت دودویی رنگ شده، سیاه باشند. بهترین حالت زمانی است که تنها یک سوم آنها سیاه باشند (و دو سوم بقیه، قرمز باشند).
کاربردها و ساختمان دادههای مرتبط
درختهای قرمز-سیاه، ضمانتی برای بدترین حالت زمان درج، حذف و جستجو میدهند. این نکته نه تنها باعث ارزشمندی آنها در کاربردهایی که زمان برای آنها حیاتی است مانند real-time application شدهاست بلکه آنها را سازنده باارزش بلوکها در سایر ساختمان دادههای استفاده شده در هندسه محاسباتی که ضمانت بدترین زمان اجرا دارند، کردهاست. درخت متوازن ساختار دیگری است که جستجو، درج و حذف را در زمان اجرای O(log n)پشتیبانی میکند. این درخت بیشتر از درخت قرمز-سیاه مرتب شدهاست که منجر به درج و حذف آهستهتر اما بازیابی سریعتر میشود. درختهای قرمز-سیاه به ویژه در برنامهنویسی تابعی ارزشمند هستند که یکی از رایجترین انواعساختار پایدار دادههای استفاده شده برای ساختن آرایههای اشتراکی و مجموعهها است. نسخه پایدار درختهای قرمز-سیاه علاوه بر زمان، نیازمند فضایی به اندازه O(log n) برای هر درج یا حذف است. درختهای قرمز-سیاه یک ایزومتری از درختهای ۲–۴ هستند. به عبارت دیگر، برای هر درخت ۲–۴، یک درخت قرمز-سیاه همتا که عناصر دادهای آن از همان مرتبه است، وجود دارد. عملیات درج و حذف در درختهای ۲–۴ هم معادل تغییر رنگ و چرخش در درختهای قرمز-سیاه هستند. این باعث میشود درختهای ۲–۴ ابزار مهمی برای درک منطق درختهای قرمز-سیاه باشند؛ و این همان دلیلی است که بسیاری از متنهای معرفی الگوریتمها، درختهای ۲–۴ را قبل از درختهای قرمز-سیاه معرفی میکنند باوجود اینکه درختهای ۲–۴ معمولاً در عمل استفاده نمیشوند. در سال ۲۰۰۸، رابرت سجویک یک نسخه سادهتر از درختهای قرمز-سیاه را معرفی کرد که Left-Leaning Red-Black Trees نامیده شد که با حذف کردن درجه آزادی نا مشخص در پیادهسازی به وجود آمده بود. LLRB یک ویژگی اضافه دارد که همه رئوس قرمز باید هنگام درجها و حذفها در سمت چپ درخت قرار بگیرند. درختهای قرمز-سیاه میتوانند برای هر مجموعهای از عملیات، به درختهای ۲–۳ یا درختهای ۲–۴ ایزومتریک باشند. درخت ۲–۴ ایزومتری در سال ۱۹۸۷ توسط سجویک معرفی شد. با درختهای ۲–۴، ایزومتری با یک «تغییر رنگ» حل شده است که در آن رنگ قرمز هر دو گره فرزند، به پدر منتقل میشود.
عملگرها
عملگرهای فقط خواندنی نسبت به درختهای دودویی ساده نیاز به تغییر ندارند چراکه یک حالت خاص از آنها میباشند ولی حذف و اضافهٔ معمولی میتواند تأثیراتی از قبیل خارج شدن از شروط اولیهٔ درختهای قرمز- سیاه داشته باشد که برای بازگردانی آن ویژگیها نیاز به تغییر رنگ و چرخش درخت دارد. اگرچه این نوع حذف واضافه پیچیدگی بسیاری دارد ولی بازهم نرخ جستجوی آن همچنان (O(logn میباشد.
اضافه کردن
اضافه کردن به وسیلهٔ پیادهسازی انجام شده در درختهای دودویی و رنگ آمیزی آنها با رنگ قرمز انجام میشود. اتفاقی که بعداً میافتد بستگی به شیوهٔ رنگ آمیزی گرههای مجاور بستگی دارد عبارت گره عمو به برادر گره والد اشاره دارد، همانند آنچه که در روابط خانوادگی مطرح است. توجه به موارد زیر لازم است:
- . ویژگی ۵ (همهٔ برگها سیاه هستند (گرههای nullهم سیاه محسوب میشوند)) همیشه باید حفظ شود.
- . ویژگی ۳ (فرزندان گره قرمز سیاه هستند) با اضافه کردن گره قرمز و تغییر رنگ گره به سیاه یا چرخش تهدید میگردد.
- . ویژگی ۴ (همهٔ مسیرها باید دارای تعداد مساوی گره سیاه باشند) با اضافه کردن یک گره سیاه تغییر رنگ فرمز به سیاه یا چرخش تهدید میشود
توجه کنید: برچسبهای N برای گره اضافه شده، P برای والد گره اضافه شده،G برای پدربزرگ گره اضافه شده و U برای عموی گره اضافه شده مورد استفاده میشود. هر مثال شامل شرحی در زیان سی++ میباشد:
class RBT{
.
.
.
BinaryNode * grandParent(BinaryNode *n){
if((n!=null) &&( n->parent!=null))
return n->parent->parent;
else
return NULL;
}
BinaryNode * uncle(BinaryNode *n){
BinaryNode *g=grandparent(n);
if(n->pareant==g->left)
return g->right;
else
return g->left;
}
}
حالت ۱ :گره جدید N ریشهٔ درخت باشد. در این حالت با تغییر رنگ به سیاه (بخاطر ویژگی ریشه باید سیاه باشد) و در هر مسیر باید یگ گره سیاه وجود داشته باشد اعتبار درخت را حفظ میکند.
void insert_case1(BinaryNode *n){
if(n->parent==null)
n->col=Black;
else
insert_case2(n);
}
حالت ۲: اگر گره والد سیاه باشد هیج کدام از دو ویژگی (هردو فرزند قرمز، سیاه هستند و تعداد راههای از هر مسیر به برگ دارای تعداد یکسان گره سیاه دارند) مورد تهدید واقع نمیشوند ولی فقط وجود دوگره قرمز اعتبار درخت را زیر سؤال میبرد (حالت ۳).
void insert_case2(BinaryNode *n){
if(n->parent->col==Black)
return;//درخت همچنان هر پنج ویژگی را دارد.
else
insert_case3(n);
}

حالت ۳:اگر هردو گره والد و عمو قرمز باشد، هردو به رنگ سیاه در میآیند و پدر آنها قرمز در میآید. (برابر ویژگی ۴). گره قرمز جدید دارای والد سیاه است. تا آن زمان که هر راه از والد /عمو که بهطور قطع از پدر بزرگ نیز عبور میکند همچنان معتبر میباشد. با این وجود G(پدر والد و عمو و پدربزرگ N) باید بررسی شود که آیا ریشهاست یا خیر (تا به رنگ سیاه درآید (ویژگی ۲) این کار را میتوان با یک متد بازگشتی انجام داد. حتی میتوان آن را به صورت یک حلقه نوشت که البته ثابت میشود این حلقه دارای تعداد مشخصی انجام عملیات چرخش است.
void insert_case3(BinaryNode *n){
BinaryNode u=uncle(n);
if((u!=null)&& )u->col==Red){
n->parent->col=Black;
u->col=Black;
g=grandparent(n);
g->col=Red;
insert_case1(g);
}else
insert_case4(n);
}
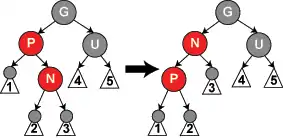
حالت ۴:اگر والد (p) قرمز باشد ولی عمو سیاه باشد همچنان گره جدید سمت راست p است و p فرزند سمت چپ G است. در این حالت، یک دوران به چپ که نقش گره جدید N را با والدش؛ P تغییر میدهد، قابلیت اجرا پیدا میکند که در آن والد قبلی با فرزندش جابجا میشود سپس والد قبلی که اکنون دوباره برچسبگذاری شده با ویژگی همه مسیرها دارای تعدا مساوی گره سیاه هستند؛ سر و کار دارد. چون بر طبق ویژگی ۴ (هر دو فرزند گره قرمز سیاه هستند) همچنان مورد تهدید بی اعتبارشدن درخت همراه است. دوران باعث میگردد تا در بعضی از مسیرها (از جمله مسیری که از زیر درخت برچسبگذاری شدهٔ ۱)عبور مینماید از گره جدیدی که قبلاً مطرح نبودهاست، عبور میکند ولی چون این گره مانند گره قبلی قرمز است، ویژگی ۴ با دوران اعتبار درخت را از بین نمیبرد.
- به همین ترتیب اگر والد (p) قرمز باشد ولی عمو سیاه باشد همچنان گره جدید سمت چپ p است و p فرزند سمت راست G است. در این حالت، یک دوران به راست روی والد(p) انجام میشود.
void insert_case4(BinaryNode *n){
BinaryNode g=grandparent(n);
if((n== n->parent->right) && (n->parent ==g->left)){
rotate_left(n->parent);
}else if((n== n->parent->left) && (n->parent ==g->right)){
rotate_right(n->parent);
n=n->right;
}
insert_case5(n);
}

حالت ۵:والد قرمز است ولی عمو سیاه میباشد و گره جدید N فرزند چپ والد P است و P فرزند چپ پدربزرگ(G)است. در این حالت رو ی پدر بزرگ(g) دوران به راست اجرا میگردد. درختی که نتیجه میشود دارای والد ی به نام P برای هردو گره G و N است .G، به عنوان ریشه، سیاه است و این تا آن زمان که فرزندش قرمز باشد پابرجاست. با تغییر رینگ P و G درخت نهایی حاصل میگردد که همهٔ ویژگیهای فوق از جمله تعداد مساوی گره سیاه در هر مسیر (به این شکل که تمامی مسیرهایی که از این سه گره عبور میکند که قبلاً از G عبور میکرده و اکنون از P عبور میکند) پابرجاست.
- به همین ترتیب اگر والد قرمز است ولی عمو سیاه میباشد و گره جدید N فرزند راست والد P است و P فرزند راست پدربزرگ(G)است. در این حالت رو ی پدر بزرگ(g) دوران به چپ اجرا میگردد.
void insert_case5(BinaryNode *n)
{
BinaryNode *g = grandparent(n);
n->parent->color = BLACK;
g->color = RED;
if ((n == n->parent->left) && (n->parent == g->left)) {
rotate_right(g);
} else {
/*یعنی :
* (n == n->parent->right) && (n->parent == g->right).
*/
rotate_left(g);
}
}
منابع
- دنیای ریاضی :درخت قرمز-سیاه
- دانشگاه ایالتی سن دیگو کلاس ۶۶۰ :نکتههایی دربارهٔ درختهای قرمز-سیاه , by Roger Whitney
- Charles E. Leiserson, Ronald L. Rivest, Thomas H. Cormen and Clifford Stein (۲۰۰۱)، «Chapter ۱۳»، مقدمهای بر الگوریتمها (ویراست ۲nd Edition)، MIT Press and McGraw-Hill، ص. ۲۷۳-۳۰۱، شابک ۰-۲۶۲-۰۳۲۹۳-۷
پیوند به بیرون
پیش نمایش
- Red Black Tree Applet، یک پیش نمایش از درخت قرمز -سیاه و سایر جستجوها
- Red Black Tree Applet، یک پیش نمایش از درخت قرمز- سیاه و avl و چرخش.
- Red/Black Tree Demonstration، یک نمایش از حذف واضافه به همراه کد جاوا.
- Red-Black Tree Animation، یک نمایش از بدترین حالت ورود
- aiSee: Visualization of a Sorting Algorithm، یک فایل گیف که نشان دهندهٔ اضافهاست (۲۰۰KB)
- Red-Black Tree Demonstration، یک نمایش از اضافه شدن با کد جاوا by David M. Howard
| در ویکیانبار پروندههایی دربارهٔ درخت سرخ-سیاه موجود است. |