درخت محدوده

درعلوم کامپیوتر، درخت محدوده یک ساختمان داده از نوع درخت مرتب است که لیستی از نقاط را نگه می‌دارد. این درخت تمامی نقاط داخل یک بازه را به‌صورت بهینه گزارش می‌دهد و معمولاً در دو بعد یا بیشتر استفاده می‌شود. درختهای محدوده توسط جان لوئیس بنتلی در سال ۱۹۷۹ معرفی شدند.[1] ساختمان داده‌های مشابه نیز به‌صورت مستقل توسط لوکر[2]، لی و وانگ[3] و ویللرد[4] معرفی شدند. درخت محدوده یک جایگزین برای درخت کی‌دی است. در مقایسه با درختهای کی‌دی، درختهای محدوده زمان جستجو سریعتری از مرتبه (O(logd n + k دارند ولی حافظه بیشتری از مرتبه (O(n logd−۱ n استفاده می‌کنند که n تعداد نقاط ذخیره شده در درخت، d بعد هر نقطه و k تعداد نقاط به دست آمده از جستجوی مورد نظر است.

تعریف
مثالی از یک درخت محدودهٔ یک بعدی.

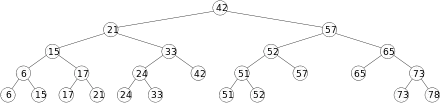
درخت محدوده روی مجموعهای از نقاط یک بعدی، یک درخت جستجوی دودویی متوازن روی آن نقاط است. نقاط در برگ‌های درخت ذخیره می‌شوند. هر گرهٔ داخلی، بیشترین مقدار ذخیره‌شده در زیر درخت چپ خود را نگه می‌دارد. یک درخت محدوده روی مجموعه‌ای از نقاط d بعدی، یک درخت جستجوی دودویی بازگشتی در چندین سطح است. هر سطح از این ساختمان داده یک درخت جستجوی دودویی روی یکی از d بعد است. اولین سطح درخت محدوده یک درخت جستجوی دودویی روی اولین مؤلفه است. هر رأس v از این درخت، یک درخت محدوده (d-1) بعدی روی (d-1) مؤلفه آخر نقاط ذخیره‌شده در زیر درخت v است.

عملیات

ساختمان

درخت محدوده یک بعدی روی مجموعه‌ای از n نقطه، یک درخت جستجو دودویی است که می‌تواند در زمان (O(n log n ساخته شود. درختهای محدوده در ابعاد بالاتر را به صورت بازگشتی این گونه می‌سازیم: ابتدا یک درخت جستجوی دودویی متوازن روی مؤلفه اول نقاط می‌سازیم. سپس، برای هر رأس v در این درخت، یک درخت محدوده (d-1) بعدی روی نقاط زیر درخت v می‌سازیم. ساختن درخت محدوده با این روش به زمان (O(n logdn نیاز دارد.

با توجه به اینکه یک درخت محدوده روی مجموعهای از نقاط دو بعدی می‌تواند در زمان (O(n log n ساخته شود، می‌توانیم روش فوق را ارتقا دهیم.[5] فرض کنید S مجموعه‌ای n تایی از نقاط دو بعدی است. اگر S فقط یک نقطه داشته باشد، برگ شامل آن نقطه را بر گردانید. در غیر این صورت، ساختار مرتبط با S؛ یک درخت محدوده یک بعدی روی مختصات y نقاط S را بسازید. xm را میانهٔ مؤلفه‌های x نقاط در نظر بگیرید. SL مجموعه نقاطی است که مختصات x شان کمتر یا مساوی xm و SR مجموعه نقاطی است که مختصات x شان بیشتر از xm است. به صورت بازگشتی vL، یک درخت محدوده دو بعدی روی SL و vR، یک درخت محدوده دو بعدی روی SR، را بسازید. رأس v را با فرزند چپ vL و فرزند راست vR بسازید. اگر در ابتدای الگوریتم این نقاط را برحسب مختصات y شان مرتب کنیم و این ترتیب هنگام جدا کردن نقاط برحسب x شان تغییر نکند، می‌توانیم ساختارهای مرتبط با هریک از درخت‌ها را در زمان خطی بسازیم. این راه، زمان ساخته‌شدن درخت محدودهٔ دوبعدی را به (O(n logn کاهش می‌دهد، که همچنین زمان ساخت درخت محدوده d بعدی نیز به مرتبهٔ (O(n logd−۱n کاهش می‌یابد.

جستجوهای بازه‌ای
یک جستجو بازه‌ای یک بعدی [x1, x2]. نقاط ذخیره‌شده در زیر درخت‌های طوسی رنگ اعلام می‌شوند. اگر (Find(x۱ و (find(x۲ در بازهٔ جستجو باشند اعلام خواهند شد.

درختهای محدوده می‌توانند برای پیدا کردن مجموعه نقاط داخل یک بازه استفاده شوند. برای پیدا کردن نقاطی که در بازه [x۱, x۲] هستند، با جستجو x۱ و x۲ شروع می‌کنیم. در یکی از رأس‌های درخت، مسیر جستجوی x۱ و x۲ جدا می‌شوند. vsplit را آخرین رأسی که در دو مسیر جستجو مشترک است در نظر می‌گیریم. به جستجوی x۱ در درخت ادامه می‌دهیم. برای هر رأس v در مسیر جستجو از vsplit تا x۱، اگر مقدار ذخیره‌شده در v بیشتر از x۱ باشد، همه نقاط زیر درخت راست v را اعلام می‌کنیم. اگر v یک برگ باشد، مقدار ذخیره‌شده در v را درصورتی‌که داخل بازهٔ جستجو باشد اعلام می‌کنیم. به‌طور مشابه، در مسیر جستجو از vsplit تا x۲. تمامی نقاط ذخیره‌شده را در زیر درخت‌های چپ رأس‌هایی که مقدارشان کمتر از x۲ است و برگ این مسیر را درصورتی‌که مقدارش در بازهٔ جستجو وجود داشت اعلام می‌کنیم.

از آنجایی که درخت محدوده، یک درخت جستجوی دودویی متوازن است، طول مسیر جستجو x۱ و x۲ از مرتبه (O(log n است. اعلام کردن تمامی نقاط ذخیره‌شده در زیر درخت یک رأس، می‌تواند با استفاده از هر الگوریتم پیمایش درخت، در زمان خطی انجام شود. در نتیجه زمان اجرای یک جستجو بازهای از مرتبه (O(log n + k است که k، تعداد نقاط داخل بازهٔ جستجو است.

بازه‌های جستجو در d بعد نیز مشابه هستند. بجای اعلام تمامی نقاط ذخیره‌شده در زیر درخت‌های مسیرهای جستجو، یک جستجو بازهای (d-1) بعدی روی ساختار مربوط به هر زیر درخت انجام می‌دهیم. سرانجام، جستجو بازهای یک بعدی انجام خواهد شد و نقاط درست اعلام خواهند شد. از آنجایی که یک جستجو d بعدی شامل (O(log n جستجو بازه‌ای (d-1) بعدی می‌شود، زمان لازم برای اجرای یک جستجو بازهای d بعدی از مرتبه (O(logdn + k است، که k تعداد نقاط در بازهٔ جستجو است. این زمان می‌تواند با استفاده از روش fractional cascading به (O(logd−۱n + k کاهش یابد.[2][4][5]

جستارهای وابسته

منابع
  1. Bentley, Jon Louis (1979). "Decomposable searching problems". Information Processing Letters. 8 (5): 244–251. doi:10.1016/0020-0190(79)90117-0. ISSN 0020-0190.
  2. Lueker, George S. (1978). "A data structure for orthogonal range queries": 28–34. doi:10.1109/SFCS.1978.1.
  3. Lee, D. T.; Wong, C. K. (1980). "Quintary trees: a file structure for multidimensional datbase sytems". ACM Transactions on Database Systems. 5 (3): 339–353. doi:10.1145/320613.320618. ISSN 0362-5915.
  4. Willard, Dan E. The super-b-tree algorithm (Technical report). Cambridge, MA: Aiken Computer Lab, Harvard University. TR-03-79.
  5. de Berg, Mark; Cheong, Otfried; van Kreveld, Marc; Overmars, Mark (2008). doi:10.1007/978-3-540-77974-2. Missing or empty |title= (help)

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.