درخت دودویی فرزند-چپ همزاد-راست
درخت دودویی فرزند چپ همزاد راست (به انگلیسی: Left-child right-sibling binary tree) (اختصاری LC-RS) در علوم رایانه، یک درخت باینری است که بازنماییای از درخت تایی (به انگلیسی: k-ary tree) است.[1] روش تبدیل یک درخت تایی دلخواه به یک درخت باینری به این صورت است که، ریشه درخت اولیه به عنوان ریشه درخت باینری در نظر گرفته میشود. سپس از ریشه شروع میکنیم و سمت چپترین فرزند هر رأس در درخت اولیه، فرزند چپ آن رأس در درخت باینری را میسازد و نزدیکترین همزاد راست در درخت اولیه، فرزند راست درخت باینری را میسازد.[2] اگر درخت اولیه مرتب شده باشد، درخت جدید درخت جستجوی دودویی خواهد بود.
درخت

درخت چیست
درخت یک گراف ساده بدون جهت است که در یکی از شروط معادل زیر صدق کند:[3]
- همبند است و دور ندارد.
- هیج دوری ندارد و اگر یک یال به آن اضافه شود یک دور ساده در آن به وجود میآید.
- همبند است و اگر یک یال آن حذف شود دیگر متصل نیست.
- همبند است و گراف کامل ۳ رأسی جزِئی از آن نیست.
- هر دو رأس در با یک مسیر سادهٔ یکتا به هم وصل میشوند.
اگر تعداد متناهی رأس داشته باشد احکام بالا با شروط زیر نیز معادل اند:
- همبند است و یال دارد.
- دور ساده ندارد و یال دارد.
فرزند
برای بررسی یک درخت ابتدا یک رأس مانند رأس V را انتخاب کرده و آن را به عنوان ریشه درخت در نظر میگیریم. حال اگر دو رأس مانند T , E به هم با یک یال متصل باشند با استفاده از تعریف فاصله که بیان میکند فاصله دو رأس از یک دیگر به میزان تعداد یالهای کوتاهترین مسیر بین آن دو رأس است (که با توجه به درخت بودن گراف مطمئن هستیم مسیر وجود دارد) تعریف میکنیم رأسی که فاصله کمتری تا رأس V که رأس ریشه است دارد پدر رأس دیگر است و دیگری فرزند آن به حساب میآید. برای مثال داریم:
۱
/ \
/ \
۲ ۳
/ \
/ \
۴ ۵
در این شکل ۱ به عنوان ریشه انتخاب شدهاست، ۲ و ۳ فرزندان ۱ هستند، ۲ فرزندی ندارد و ۴ و ۵ فرزندان ۳ هستند. این درخت را به گونهای دیگر نیز میتوان نشان داد.
۲
|
۱
|
۳
/ \
۴ ۵
در این شکل نیز همان گراف قبل نمایش داده شده با این تفاوت که در این شکل ۲ به عنوان ریشه درخت انتخاب شدهاست.
همزاد
به دو رأس مانند T , E همزاد میگوییم اگر پدر مشترک داشته باشند (پدر هر دو یک رأس باشد). به عبارتی دیگر به دو فرزند یک پدر همزاد گوییم. برای مثال در همان گراف قبل داریم :
۱
/ \
/ \
۲ ۳
/ \
/ \
۴ ۵
رئوس ۲ و ۳ که هردو دارای پدر مشترک ۱ هستند با یک دیگر همزاد هستند. به طریق مشابه نیز میتوان گفت رئوس ۴ و ۵ نیز با یک دیگر همزاد هستند.
درخت تایی
در نظریه گراف به یک درخت تایی گفته میشود اگر هر رأس حداکثر به تعداد بچه داشته باشد. برای مثال حالت خاصی از درخت تایی حالت است که به آن درخت باینری گفته میشود.[4]
۱
/ | \
/ | \
/ | \
۲ ۴ ۳
/ / | \
/ / | \
۸ ۷ | ۵
۶
در این شکل یک درخت تایی به ازای است. چون در آن هر رأس حداکثر ۳ بچه دارد.
درخت دودویی فرزند چپ همزاد راست چیست؟
در یک درخت باینری مانند میتوان هر رأس را با دو اشاره گر در نظر گرفت. ابتدا در این درخت ریشه را تعریف میکنیم. سپس برای هر رأس از درخت یک اشارهگر به اولین فرزند که به آن فرزند چپ میگوییم و اشارهگر دوم را به اولین همزاد بعد از خود در درخت که به اصطلاح همزاد راست گفته میشود تعریف میکنیم. حال برای پیدا کردن فرزند ام یک رأس (برای مثال رأس ) با توجه به در اختیار داشتن فرزند چپ که اولین فرزند است و در اختیار داشتن همزاد راست هر رأس (که در اینجا همزاد راست هر فرزند مد نظر است) میتوان با پیمایش فرزندان فرزند این رأس را پیدا کرد:
procedure kth-child(V, n):
child ← V.child
while n ≠ 0 and child ≠ nil:
child ← child.next-sibling
n ← n − 1
return child
که کد این پیمایش در زبان پایتون به قرار زیر است:
def kth-child(V, n):
child = V.child
while n != 0 and child is not None:
child = child.nex-sibling
n -= 1
return child
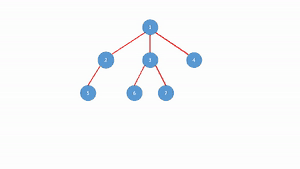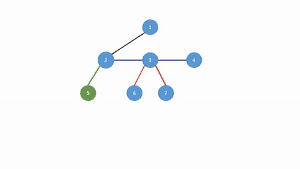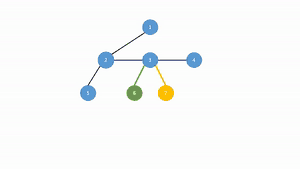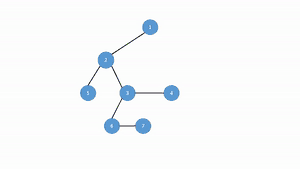
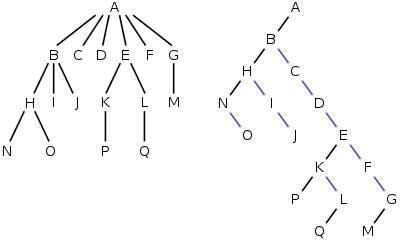
در شکل روبرو در هر مرحله (الگوریتم از ریشه شروع میشود) فرزند چپ و یال واصل به پدر به رنگ سبز و همزادهای آن همگی به رنگ زرد در میآیند. حال هر یالی که به رنگ زرد است حذف میشود و جایگزین آن به فرزند چپ پدر متصل میشوند. در انتها نیز درخت به لحاظ ظاهری مرتب میشود.
کد الگوریتم بالا را میتوان به زبان جاوا به شکل زیر نوشت:
public Child kth-child(V, n){
Child Child = V.Child ;
while(n != 0 && child != null){
Child = Child.nex-sibling ;
n -- ;
}
return child ;
}
که تنها باید به این نکته توجه کرد که در صورت وجود امین فرزند برنامه به عنوان خروجی آن را بازگردانی میکند و در غیر این صورت خروجی تهی خواهد بود.
پروسه تبدیل یک درخت تایی به یک درخت دودویی فرزند چپ همزاد راست گاهی با نام تبدیل کنوت (به انگلیسی: Knuth transform) شناخته میشود.[5]
میتوان الگوریتمی به قرار زیر ارائه داد تا با استفاده از آن بتوانیم یک درخت تایی را به یک درخت دودویی فرزند چپ همزاد راست تبدیل کنیم. در این الگوریتم ابتدا ریشه درخت تایی را به عنوان ریشه این درخت نیز انتخاب میکنیم. حال برای هر رأس در درخت دودویی فرزند چپ همزاد راست مانند فرزند چپ در درخت تایی را فرزند چپ و همزاد راست در درخت تایی را فرزند راست در این درخت قرار میدهیم.[6]
حال میخواهیم این الگوریتم را در فرایند تبدیل یک درخت به یک درخت دودویی فرزند چپ همزاد راست بررسی کنیم و در این الگوریتم در شکل اول درخت باینری را مشاهده میکنیم که قرار است الگوریتم بر روی آن اجرا شود. هر رأس در این الگوریتم دارای دو نشانه گر است که با استفاده از آنها یالها در درخت نهایی رسم خواهند شد که آن دو نشانه گر فرزند چپ. همزاد راست رأس هستند.
۱
/|\
/ | \
/ | \
۲ ۳ ۴
/ \ |
۵ ۶ ۷
/ \
۸ ۹
حال در صورتی که برای هر رأس تنها دو اشارهگر یعنی فرزند چپ یا اولین فرزند و همزاد راست یا اولین خواهر یا برادر را به یک دیگر از طریق یال وصل کنیم و باقی مانده یالها را از درخت پاک کنیم خواهیم داشت:
۱
/
/
/
۲ ---- ۳ ---- ۴
/ /
۵ ---- ۶ ۷
/
۸ ---- ۹
که اگر دقت کنیم شکل حاصل یک درخت دودویی فرزند چپ همزاد راست خواهد بود. کافی است خط چینها را که به درخت اضافه کردهایم و عمودی هستند را ۴۵ درجه دوران بدهیم.
۱
/
/
/
۲
/ \
/ ۳
۵ \
\ \
\ ۴
۶ /
۷
/
۸
\
۹
مثالی دیگر از این الگوریتم را میتوانید در شکل زیر مشاهده کنید:
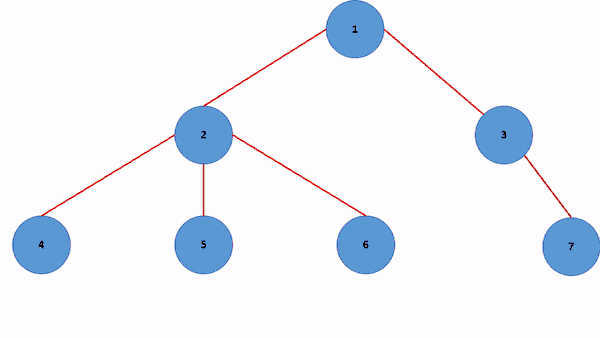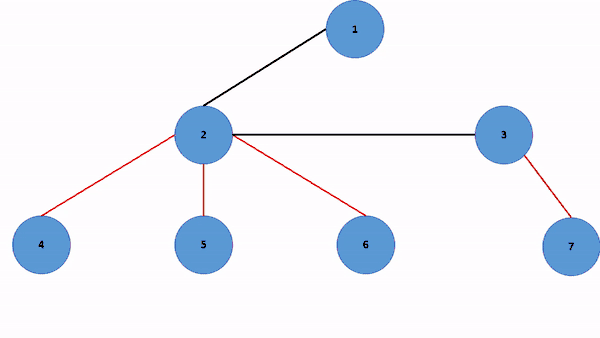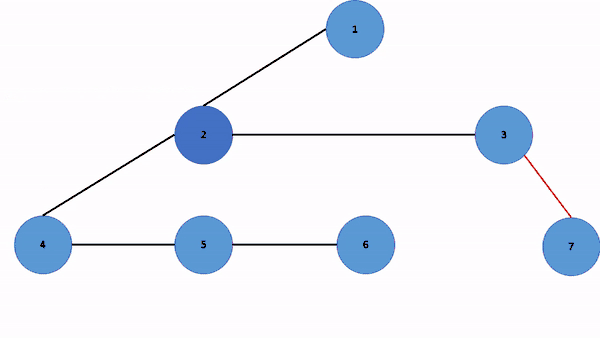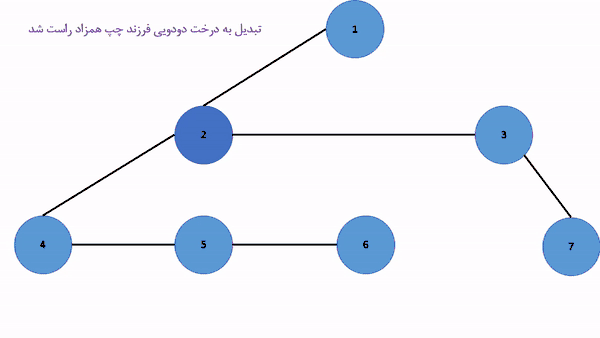
بازگردانی الگوریتم
در این قسمت میخواهیم حالت بازگشت از یک درخت دودویی فرزند چپ همزاد راست به یک درخت تایی را بررسی کنیم. ابتدا ریشه درخت را در جایگاه ریشه درخت خروجی قرار میدهیم. (باید توجه کرد در الگوریتم قبلی مکان ریشه تغییری ایجاد نمیشد) حال در هر رأس مانند تا زمانی که میتوان به سمت راست حرکت کرد تمام رئوس فرزندان پدر یا به عبارتی دیگر همزادهای هستند. حال تمام این رئوس را به عنوان فرزندان پدر اضافه میکنیم. حال به رأس بازگشته و فرزند چپ را در صورت وجود به فرزندان آن اضافه میکنیم و همین الگوریتم را برای فرزند چپ انجام میدهیم .
def rev-LCRS(node, Tree):
if node.root :
Tree.root = node
temp = node
while temp.rightChild is not None:
Tree.search(node).parent.addChild(temp.rightChild)
temp = temp.rightChild
if node.leftChild is not None:
Tree.search(node).addChild(node.leftChild)
return rev-LCRS(node.leftChild, Tree)
یا میتوان به زبان جاوا به شکل زیر بیان کرد:
public void rev-LCRS(Node node, Tree tree){
if (node.root) {
tree.root = node;
}
temp = node;
while (temp.rightChild is not None){
Tree.search(node).parent.addChild(temp.rightChild);
temp = temp.rightChild;
}
if (node.leftChild is not None){
Tree.search(node).addChild(node.leftChild);
return rev-LCRS(node.leftChild, Tree);
}
}
کاربرد
در بازنمایی درخت دودویی فرزند چپ همزاد راست بسیار کارآمدتر از شیوه نمایش سنتی یک درخت است اما هزینهای که برای یافتن یک فرزند بخصوص از یک رأس مانند میپردازیم بسیار زیاد است چون همانطور که در قسمت قبل نیز توضیح داده شد برای این کار باید فرزندان رأس پیمایش شوند که در صورت اینکه درخت تایی باشد هزینه این الگوریتم از خواهد بود که در صورت زیاد بودن مقدار میتواند هزینهای سنگین برای یافتن یک فرزند دربرداشته باشد. میتوان گفت این روش در مواردی کارآمد است که:[6]
- نگرانیهایی مبنی بر کارایی حافظه داریم.
- دسترسی تصادفی به فرزندان در الگوریتم مورد نیاز نباشد.
در زمانی نگران مورد یک خواهیم بود که با حجم زیادی از اطلاعات برخورد داریم، برای مثال برای ذخیرهسازی درخت تبارزایی که میتواند حجم زیادی داشته باشد استفاده از این روش ممکن است کارآمد باشد.[7]
منابع
- Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, and Clifford Stein (2001). Introduction To Algorithms (2nd ed.). MIT Press. pp. 214–217. ISBN 978-0-262-03293-3.
- Paul E. Black, Left child-right sibling binary tree at the NIST Dictionary of Algorithms and Data Structures
- Heaps
- Black, Paul E. (20 April 2011). "perfect k-ary tree". U.S. National Institute of Standards and Technology. Retrieved 10 October 2011.
- Computer Data Structures. John L. Pfaltz.
- [[[:en:Left-child right-sibling binary tree]] "Left-child_right-sibling_binary_tree"] Check
|نشانی=value (help). - "What is the left-child, right-sibling representation of a tree? Why would you use it?". stackoverflow.com. Retrieved 2016-12-12.