هرم (ساختمان داده)
در علوم رایانه، هرم (Heap) داده ساختاری است که بر اساس درختها پیادهسازی میشود. هرم یک داده ساختار بهینه برای پیادهسازی یک داده گونه انتزاعی(abstract data type) به نام صف اولویت دار است. هرمها میتوانند به شکلهای مختلفی پیادهسازی شوند. یکی از رایجترین پیادهسازیها، هرم دودویی است که با استفاده از درخت دودویی مدل میشود.

هرم دودویی دو نوع دارد:
- هرم بیشینه (Max heap)
- هرم کمینه (Min heap)
برای الگوریتم مرتبسازی هرمی از هرم بیشینه و برای پیادهسازی صف اولویت دار معمولاً از هرم کمینه استفاده میشود.[1]
در هر دو نوع، مقادیر گرهها از خاصیت هرم پیروی میکنند. خاصیت هرم بیشینه این است که به ازای هر گره، مقدار موجود در والدش (parent) در صورت وجود بزرگتر مساوی با مقدار آن گره است؛ بنابراین عنصر بیشینه در ریشه درخت (root) قرار دارد.

خاصیت هرم کمینه، برعکس هرم بیشینه است به این صورت که به ازای هر گره، مقدار موجود در والدش (parent) در صورت وجود کوچکتر مساوی با مقدار آن گره است؛ بنابراین عنصر کمینه در ریشه درخت (root) قرار دارد.
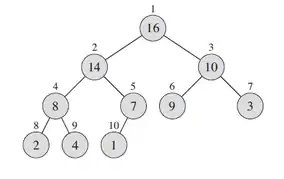
در هرمهای دودویی روابطی بین اندیس هر گره (i)، والد ((parent(i)، فرزند چپ ((left(i) و فرزند راست ((right(i) آن در آرایه مرتب شده وجود دارد:
- [ Parent(i) = arr[ (i-1) / 2
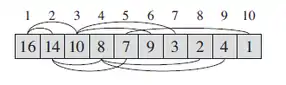
- [ Left(i) = arr[ (2*i) + 1
- [ Right(i) = arr[ (2*i) + 2
اگر هرم را به چشم یک درخت ببینیم ارتفاع ( height ) برای هر گره ، اندازه طولانیترین مسیر نزولی از آن گره تا یکی از برگها و ارتفاع هرم معادل با ارتفاع گره ی ریشه خواهد بود .بنابراین در هرمی دودویی متشکل از n عنصر ، ارتفاع هرم ( Θ( log n است.[2] همچنین عمق (depth) هر گره برابر با طول مسیر از آن گره تا گرهٔ ریشه و عمق هرم معادل با عمق آخرین لایه از برگها خواهد بود.
توابعی که بر روی هرمها پیادهسازی میشوند عبارتند از:
توابع پایه
- find-max و find-min: بیشترین عنصر هرم بیشینه یا کمترین عنصر هرم کمینه را برمیگرداند.
- insert: یک گرهٔ جدید را به هرم اضافه میکند.
- extract-max یا extract-min: پس از حذف عنصر کمینه در هرم کمینه (یا حذف عنصر بیشینه از هرم بیشینه) از هرم، آن را برمیگرداند.
- delete-max یا delete-min: ریشهٔ هرم (عنصر بیشینه در هرم بیشینه یا عنصر کمینه در هرم کمینه) را پاک میکند.
- replace: عنصر ریشه را pop میکند و بهجای آن یک گره جدید push میکند.
توابع ایجاد
- create-heap: که یک هرم خالی میسازد.
- heapify: هرم متناظر با آرایه داده شده را تشکیل میدهد.
- merge: دو هرم را ترکیب میکند و یک هرم جدید میسازد که عناصر هر دو را داشته باشد و هرمهای اولیه نیز حفظ میشوند.
- meld: دو هرم را ترکیب میکند و یک هرم جدید میسازد که عناصر هر دو را داشته باشد؛ سپس دو هرم اولیه حذف میشوند.
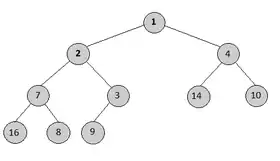 نمونه ای از هرم دودویی کمینه
نمونه ای از هرم دودویی کمینه
توابع بازرسی
- size: تعداد گرههای هرم را برمیگرداند.
- is-empty: اگر هرم خالی باشد true و در غیر این صورت false برمیگرداند.
توابع داخلی
- increase-key یا decrease-key: مقدار یک گره در هرم را به روز میکند.
- max-heapify-up یا min-heapify-down: تا جایی که نیاز باشد یک گره را در هرم بالا یا پایین میبرد (پس از insert و delete و replace)
داده ساختار هرم نباید با مفهوم Heap که برای اختصاص پویای حافظه به کار میرود اشتباه شود. بعضی از زبانهای برنامهنویسی مانند لیسپ برای این شیوهٔ اختصاص حافظه از داده ساختار هرم استفاده میکنند. هرمها معمولاً به صورت آرایه پیادهسازی میشوند و نیاز به اشاره گر ندارند.
Build_Max_Heap(A)
A.heap-size = A.length
for i = [A.length / 2] downto 1
Max-Heapify( A , i )Max-Heapify(A,i)
l = Left(i)
r = Right(i)
if l <= A.heap-size and A[l] > A[i]
largest = l
else
largest = i
if r <= A.heap-size and A[r] > A[largest]
largest = r
if largest != i
exchange A[i] with A[largest]
Max-Heapify( A , largest )
- هرم ۲–۳
- بیپ (en)[3]
- هرم دودویی
- هرم فیبوناچی
- هرم چپگرا[4]
- هرم اریب[5]
- هرم بی[6]
- هرم دو جمله ای[7]
- هرم مبنایی[8]
مقایسهٔ محدودیتهای نظری انواع هرم
پیچیدگی زمانی تعدادی از انواع هرم برای تابعهای مختلف در جدول زیر آمدهاست. خانههای ستاره دار نشان دهندهٔ زمان سرشکن است و خانههایی که دو ستاره دارند نشاند دهندهٔ این است که n اندازهٔ هرم بزرگتر است.
| Operation | Binary | Binomial | Fibonacci heap | Pairing heap | Brodal queue |
|---|---|---|---|---|---|
| create-heap | Θ(۱) | Θ(۱) | Θ(۱) | ? | O(1) |
| findMin | Θ(۱) | O(log n) | Θ(۱) | O(1)* | O(1) |
| deleteMin | Θ(log n) | Θ(log n) | O(log n)* | O(log n)* | O(log n) |
| insert | Θ(log n) | O(log n) | Θ(۱) | O(1)* | O(1) |
| decreaseKey | Θ(log n) | Θ(log n) | Θ(۱)* | O(log n)* | O(1) |
| merge | Θ(n) | O(log n)** | Θ(۱) | O(1)* | O(1) |
کاربردها
داده ساختار هرم کاربردهای زیادی دارد که برخی از آنها عبارتند از:
- مرتبسازی هرمی: یکی از بهترین شیوههای مرتبسازی است که «درجا» (in place) انجام میشود و در بدترین حالت نیز مرتبه زمانی خطی دارد.
- الگوریتم انتخاب: برای یافتن عنصر بیشینه، کمینه، میانه و kامین عنصر در زمان خطی به کار میرود.
- الگوریتمهای گراف: با استفاده از هرم به عنوان زمان بهینهٔ پیمایش، زمان اجرا به صورت چند جملهای کاهش مییابد. این الگوریتمها برای مواردی مانند الگوریتم پریم و الگوریتم دیکسترا استفاده میشوند.
- صف اولویت دار: برای پیادهسازی صف اولویت دار معمولاً از هرم کمینه استفاده میشود.
پیادهسازی
- ++C: در کتابخانهٔ این زبان برنامهنویسی تابعهایی مانند make_heap, push_heap و pop_heap برای هیپها پیادهسازی شدهاست. در این توابع، دادهها به صورت آرایه داده میشوند و از تبدیل array-to-heap استفاده میشود.
- Java: در جاوا ۲ برای پیادهسازی هیپ دوتایی از کلاس java.util.PriorityQueue<E> استفاده میشود.
- پایتون (زبان برنامهنویسی): در این زبان از ماژول heapq استفاده میشود که یک هیپ دودویی را به کمک یک صف اولویت دار پیادهسازی میکند.
- PHP: که دو تابع SplMaxHeap و SplMinHeap را برای پیادهسازی maxheap و minheap دارد.
- Perl: از سیپن برای پیادهسازی هیپهای فیبوناتچی و دوتایی استفاده میکند.
- Go: این زبان یک بستهٔ هیپ دارد که در پیادهسازی از آن استفاده میکند.
منابع
- (Introduction to Algorithms - 3rd Edition - (CLRS.
- (Introduction to Algorithms-3rd Edition-(CLRS.
- en:Beap Beap
- en:Leftist tree Leftist heap
- en:Skew heap Skew heap
- en:B heap B heap
- en:Binomial heap Binomial heap
- en:Radix heap Radixheap
[[[:en:Binary|heap:]]]