ارتفاع موج مشخصه
ارتفاع موج مشخصه از نظر سنتی در اقیانوسنگاری فیزیکی، به عنوان میانگین ارتفاع موج یکسوم بزرگترین موجها (H1/3) تعریف میشود. اکنون معمولاً آن را به صورت چهار برابر انحراف معیار تراز سطح آب (یا به عبارت دیگر، چهار برابر جذر میانگین مربعات گشتاور مرتبهٔ صفر طیف موج) در نظر میگیرند.[1] نماد Hm0 معمولاً برای تعریف دوم به کار میرود.
منشأ و تعریف
تعریف اصلی بر اساس پژوهش والتر مانک در دوران جنگ چهانی دوم معرفی شد.[2] ارتفاع موج مشخصه برای تبیین ارتفاع تخمین زده شده توسط «مشاهدهگر آزموده» تعریف شد. اکنون آن را به عنوان معیاری برای ارتفاع امواج اقیانوسی در نظر میگیرند.
توزیع آماری ارتفاع تکموجها
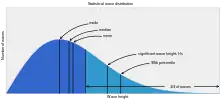
ارتفاع موج مشخصه که از نظر علمی، با Hs یا Hsig نمایش داده میشود، پارامتر مهمی برای توزیع آماری امواج اقیانوسی است. ارتفاع بیشتر موجهای متداول کمتر از Hs است. بنابراین موج مشخصه بسامد زیادی ندارد. هرچند که ممکن است موجی با ارتفاع بسیار بیشتر از موج مشخصه نیز موجود باشد.
عموماً توزیع آماری ارتفاع تکموجها با توزیع رایلی تقریب زده میشود.[3] برای نمونه، اگر ارتفاع موج مشخصه ۱۰ متر باشد، از نظر آماری:
- ۱ در ۱۰ بزرگتر از ۱۰٫۷ متر هستند
- ۱ در ۱۰۰ بزرگتر از ۱۵٫۱ متر هستند
- ۱ در ۱۰۰۰ بزرگتر از ۱۸٫۶ هستند
بنابراین ممکن است موجی با ارتفاع تقریباً دو برابر موج مشخصه مشاهده شود.
اندازهگیری
بیشتر دستگاههای اندازهگیری، ارتفاع موج مشخصه را از طیف موج تخمین میزنند؛ ولی آلتیمترهای ماهوارهای به دلیل اختلاف زمان برگشت از تاج و قعر موج در ناحیهٔ زیر پوشش، آن را مستقیماً اندازهگیری میکنند. بیشترین ارتفاع موج اندازهگیری شده توسط یک ماهواره، در طوفانی در اقیانوس اطلس شمالی در سال ۲۰۱۱ به میزان ۲۰٫۱ متر است.[5]
جستارهای وابسته
پانویس
- Holthuijsen, Leo H. (2007). Waves in Oceanic And Coastal Waters. Cambridge University Press. p. 70. ISBN 978-0-521-86028-4.
- Denny, M.W. (1988). Biology and the Mechanics of Wave-swept Shores. Princeton, New Jersey: Princeton University Press. ISBN 0-691-08487-4.
- Tayfun, Aziz (1980). "Narrow-band nonlinear sea waves". Journal of Geophysical Research. 85 (C3): "1543–1552". Bibcode:1980JGR....85.1548T. doi:10.1029/jc085ic03p01548.
- Dean, Robert G.; Dalrymple, Robert A. (1991). Water Wave Mechanics for Engineers and Scientists. World Scientific. p. 193. ISBN 978-981-02-0421-1.
- J. Hanafin, Y. Quilfen, F. Ardhuin, D. Vandemark, B. Chapron,H. Feng, J. Sienkiewicz, P. Queffeulou, M. Obrebski, B. Chapron, N. Reul, F. Collard, D. Cormand, E. B. de Azevedo, D. Vandemark,and E. Stutzmann (2012).

