کمژرفایی
در دینامیک سیالات، کمژرفایی موج، پدیدهای است که باعث تغییر ارتفاع موج در هنگام ورود موج سطحی به آب کمعمق میشود. دلیل این پدیده، تغییر سرعت گروه (که سرعت انتقال انرژی موج نیز هست) با عمق آب میباشد. در شرایط پایدار، کاهش سرعت انتقال باید با افزایش چگالی انرژی جبران شود تا شار انرژی ثابت بماند.[2] طول موجهای کمژرفا نیز کاهش مییابد، ولی بسامد ثابت میماند.

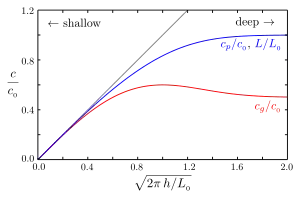
مقادیر با استفاده از شتاب گرانشی g و دوره T، بیبعد شدهاند. طول موج آب عمیق L0 = gT2/(2π) و سرعت فاز آب عمیق c0 = L0/Tاست. خط خاکستری مربوط با حد آب کمعمق cp =cg = √(gh) است. سرعت فاز – و در نتیجه همچنین طول موج L = cpT – به صورت یکنواخت با کاهش عمق، کم میشود. ابتدا سرعت گروه تا ۲۰٪ نسبت به مقدار آن در آب عمیق (از cg = 1/212c0 = gT/(4π)) افزایش مییابد و سپس در اعماق کمتر کاهش مییابد.[1]
در آبهای کمعمق و خطوط تراز موازی، در هنگام ورود گروه موج به آب کمعمقتر، ارتفاع امواج غیر شکنا افزایش مییابد.[3] این امر به ویژه در سونامی آشکار است که در آن ارتفاع موج در هنگام نزدیک شدن به یک خط ساحلی به صورت قابل توجهی افزایش مییابد و نتایج مخربی را به بار میآورد.
روابط ریاضی

شار انرژی موج غیر شکنا که حاصلضرب چگالی انرژی موج در سرعت گروه میان دو شعاع موج است، یک کمیت پایسته است. در شرایط پایدار، مجموع انتقال انرژی باید در امتداد یک شعاع موج ثابت باشد:[4]
که s محور موازی شعاع موج و شار انرژی در واحد طول تاج موج است. کاهش سرعت گروه باید با افزایش چگالی موج E جبران شود. این پدیده را میتوان به عنوان ضریب کمژرفایی متناسب با ارتفاع موج در آب عمیق رابطهسازی کرد.[5]
بردار عدد موج موضعی، شیب تابع فاز است:
و بسامد زاویهای متناسب با نرخ تغییرات موضعی آن است:
- .
با سادهسازی به یک بعد و مشتقگیری متقاطع، بهسادگی دیده میشود که بر اساس تعریف بالا نرخ تغییرات عدد موج با همگرایی بسامد در امتداد یک شعاع، در تعادل است:
- .
با فرض شرایط پایدار ()، این معادله نتیجه میدهد که تاج موج پایسته است و بسامد باید در امتداد شعاع موج ثابت بماند . با ورود موج به آب کمعمقتر کاهش سرعت گروه باعث کاهش طول موج میشود؛ زیرا حد آب کمعمق رابطه پراکنش برای سرعت فاز موج
تحکم میکند که
جستارهای وابسته
- نظریه موج ایری
- موج شکنا
- پاشندگی (امواج آب)
- امواج سطح اقیانوس
- معادلات آب کمعمق
- سد ساحلی
- Waves and shallow water
- ارتفاع موج
- عدد اورسل
منابع
- Wiegel, R.L. (2013). Oceanographical Engineering. Dover Publications. p. 17, Figure 2.4. ISBN 0-486-16019-X.
- Longuet-Higgins, M.S.; Stewart, R.W. (1964). "Radiation stresses in water waves; a physical discussion, with applications" (PDF). Deep Sea Research and Oceanographic Abstracts. 11 (4): 529–562. Archived from the original (PDF) on 12 June 2010. Retrieved 18 March 2016.
- WMO (1998). Guide to Wave Analysis and Forecasting (PDF). 702 (2 ed.). World Meteorological Organization. ISBN 92-63-12702-6.
- Burnside, W. (1915). "On the modification of a train of waves as it advances into shallow water". Proceedings of the London Mathematical Society. Series 2. 14: 131–133. doi:10.1112/plms/s2_14.1.131.
- Dean, R.G.; Dalrymple, R.A. (1991). Water wave mechanics for engineers and scientists. Advanced Series on Ocean Engineering. 2. Singapore: World Scientific. ISBN 978-981-02-0420-4.



