الگوریتم خدا

بحث‌هایی که پیرامون حل پازل مکعب روبیک بوده‌است، سرچشمهٔ پیدایش نظریه‌ای به نام الگوریتم خدا شده‌است،[1] هرچند که بر روی سایر پازل‌های ترکیبی و بازی‌ریاضی‌ها نیز قابل اجرا است.[2] در واقع، الگوریتم خدا به هر الگوریتمی که راه‌حلی با کمترین تعداد حرکات ممکن را ارائه می‌دهد، تلقی می‌شود. ایده پیدایش این الگوریتم، این است که می‌گوید یک موجود واقف بر همه چیز (omniscient being) وجود دارد که برای هر موقعیت داده شده‌ای، از یک گام بهینه برای آن موقعیت آگاه است.

تعریف و راه‌حل

این نظریه، برای پازل‌هایی قابل اجرا است که تعداد وضعیت‌های متفاوتی که می‌تواند داشته باشد، محدود است، با مجموعه‌ای از حرکات نسبتاً کوچک و معلوم که ممکن است روی این وضعیت‌ها قابل اجرا باشند و منجر به یک وضعیت جدید شوند. حل کردن یک پازل یعنی دستیابی به یک وضعیت معین نهایی که ممکن است فقط و فقط یک تک وضعیت یا یک عضو از مجموعه‌ای از وضعیت‌ها باشد.

یک راه‌حل را بهینه می‌گوییم اگر دنبالهٔ حرکات آن، کوتاهترین حالت ممکن باشد. این تعداد حرکات، با عنوان عدد خدا[3] یا به شکل رسمی‌تر، مقدار کمین‌بیش نیز شناخته می‌شوند. در نتیجه، برای یک پازل، الگوریتم خدا، الگوریتمی است که پازل را فقط با راه‌حل‌های بهینه حل می‌کند.

مثال‌ها

پازل‌های n تایی

پازل ۱۵ تایی، در بدترین حالت می‌تواند با ۸۰ حرکت تک خانه‌ای یا ۴۳ حرکت چند خانه‌ای[4] حل شود. برای حالت کلی آن که پازل n تایی است، از آنجایی که مسئلهٔ پیدا کردن یک راه‌حل بهینه برای آن، ان‌پی سخت است،[5] هنوز مشخص نیست که آیا یک الگوریتم خدای کاربردی برای آن وجود دارد یا خیر، اگرچه بعید به نظر می‌رسد.

برج‌های هانوی

برای پازل برج‌های هانوی، برای هر تعداد دیسک داده شده، یک الگوریتم خدا وجود دارد، هرچند تعداد حرکات با افزایش تعداد دیسک‌ها به صورت نمایی زیاد می‌شود.[6]

مکعب روبیک

در سال ۱۹۹۷، ریچارد کُرف الگوریتمی برای پیدا کردن راه‌حل‌های بهینه برای حل پازل مکعب روبیک ارائه کرد.[7] اگرچه در سال ۱۹۸۰، دیوید سینگ‌مستر حدس زده بود که کران بالای تعداد حرکات لازم برای حل مکعب روبیک ۲۰ است، ولی در سال ۱۹۹۵، کشف شد که کران پایین برای تعداد حرکات لازم برای حل یک مکعب روبیک ۲۰ است و در سال ۲۰۱۰ محاسباتی که توسط کامپیوترهای بزرگ انجام شد، ثابت کرد که برای حل هیچ وضعیتی به بیش از ۲۰ حرکت نیاز نیست.[8] بنابراین، عدد خدا برای مکعب روبیک، ۲۰ است.

عدد خدا

برای مکعب روبیک، عدد خدا، بیشینه تعداد حرکات لازم برای حل هر یک از ۴۳٬۲۵۲٬۰۰۳٬۲۷۴٬۴۸۹٬۸۵۶٬۰۰۰ ترکیب‌های روبیک است و ثابت شده‌است که این عدد، برابر ۲۰ است. این عدد ممکن است کوچک بنظر برسد، اما به صورت تئوریک، این عدد باید حتی کمتر باشد. تنها حدود ۴۹۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰ ترکیب نیاز به تمام ۲۰ حرکت برای حل شدن دارد. هرچند که ۴۹۰ میلیون هم عدد بزرگی است، اما نسبت آن به ۴۳ کوینتیلیون وضعیت ممکن، تنها حدود ۰٫۰۰۰۰۰۱۱۳۲۸۹۵۵٪ است. یعنی احتمال اینکه بتوان به صورت تصادفی، وضعیتی تولید کرد که فقط و فقط در ۲۰ حرکت حل شود، نه بیشتر و نه کمتر، حدود ۱ در بیلیون است. اگرچه، تعداد ترکیب‌هایی که در ۱۹ حرکت حل می‌شوند، تقریباً ۱٫۵ کوینتیلیون است. به عبارتی، عدد خدا برای روبیک بیشتر به ۱۹ نزدیک است تا ۲۰، ولی اگر غیرممکن باشد حتی یک ترکیب را با کمتر از ۲۰ حرکت حل کرد، عدد خدا ۲۰ خواهد بود.[9]

جدول زیر، تعداد وضعیت‌ها را برای فاصله‌های مختلف نشان می‌دهد:[8]

فاصله تعداد وضعیت‌ها
۰ ۱
۱ ۱۸
۲ ۲۴۳
۳ ۳٬۲۴۰
۴ ۴۳٬۲۳۹
۵ ۵۷۴٬۹۰۸
۶ ۷٬۶۱۸٬۴۳۸
۷ ۱۰۰٬۸۰۳٬۰۳۶
۸ ۱٬۳۳۲٬۳۴۳٬۲۸۸
۹ ۱۷٬۵۹۶٬۴۷۹٬۷۹۵
۱۰ ۲۳۲٬۲۴۸٬۰۶۳٬۳۱۶
۱۱ ۳٬۰۶۳٬۲۸۸٬۸۰۹٬۰۱۲
۱۲ ۴۰٬۳۷۴٬۴۲۵٬۶۵۶٬۲۴۸
۱۳ ۵۳۱٬۶۵۳٬۴۱۸٬۲۸۴٬۶۲۸
۱۴ ۶٬۹۸۹٬۳۲۰٬۵۷۸٬۸۲۵٬۳۵۸
۱۵ ۹۱٬۳۶۵٬۱۴۶٬۱۸۷٬۱۲۴٬۳۱۳
۱۶ حدود ۱٬۱۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰
۱۷ حدود ۱۲٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰
۱۸ حدود ۲۹٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰
۱۹ حدود ۱٬۵۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰
۲۰ حدود ۴۹۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰
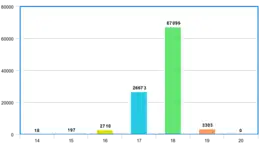
نحوه پراکندگی تعداد وضعیت‌های تصادفی بر حسب تعداد حرکات مورد نیاز برای حل بهینه هربرت کوکیمبا

.

در سال ۲۰۰۹، هربرت کوکیمبا (Herbert Kociemba) از برنامه Cube Explorer و یک کامپیوتر با پردازنده Intel Core i7-920 (که اولین پردازنده Core i7 بود) و ۶ گیگابایت حافظه رم استفاده کرد تا ۱۰۰٬۰۰۰ وضعیت تصادفی را به صورت بهینه حل کند. به‌طور میانگین، برنامه هر روز ۷٬۰۰۰ مکعب را حل می‌کرد. در نهایت، میانگین طول حل بهینهٔ این مکعب‌ها، ۱۷٫۷ حرکت بود.[10]

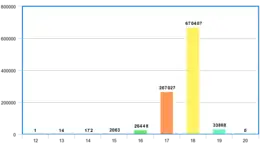
نحوه پراکندگی تعداد وضعیت‌های تصادفی بر حسب تعداد حرکات مورد نیاز برای حل بهینه توماس روکیکی

.

در ژانویه ۲۰۱۰ نیز توماس روکیکی (Tomas Rokicki) حتی ۱٬۰۰۰٬۰۰۰ مکعب را به صورت بهینه حل کرد.[10]

همان‌طور که در نمودارها مشخص است، توزیع‌های به دست آمده توسط توماس روکیکی نیز مشابه هربرت کوکیمبا است.[10]

تاریخچه عدد خدا

تحقیقات روی عدد خدا در سال ۱۹۸۱ آغاز شد، هنگامی که مارون تیستلثویت، با استفاده از الگوریتم پیچیده‌ای که خودش ابداع کرده بود، ثابت کرد که برای حل هر ۴۳ کوینتیلیون ترکیب مختلف مکعب روبیک، ۵۲ حرکت کافی است. به مرور زمان، متدهای بهینه‌تر برای حل این تعداد عظیم از ترکیب‌های محتمل در حرکات کمتر ابداع شد.[9]

جدول زیر، تغییرات کران بالا و پایین عدد خدا برای مکعب روبیک را در گذر زمان نشان می‌دهد:[8]

تاریخ کران پایین کران بالا اختلاف یادداشت‌ها و پیوندها
ژوئیه ۱۹۸۱ ۱۸ ۵۲ ۳۴ مارون تیستلثویت (Morwen Thistlethwaite) ثابت کرد ۵۲ حرکت کافی است.
دسامبر ۱۹۹۰ ۱۸ ۴۲ ۲۴ هانس کلوسترمان (Hans Kloosterman) تعداد حرکات را به ۴۲ بهبود داد.
می ۱۹۹۲ ۱۸ ۳۹ ۲۱ مایکل رید (Michael Reid) نشان داد ۳۹ حرکت همواره کافی است.
می ۱۹۹۲ ۱۸ ۳۷ ۱۹ دیک وینتر (Dik Winter) آن را به ۳۷ حرکت کاهش داد، آن هم تنها یک روز بعد!
ژانویه ۱۹۹۵ ۱۸ ۲۹ ۱۱ مایکل رید با آنالیز الگوریتم دو فازه‌یِ کوکیمبا، کران بالا را به ۲۹ حرکت کاهش داد.
ژانویه ۱۹۹۵ ۲۰ ۲۹ ۹ مایکل رید ثابت کرد وضعیت "superflip" (گوشه‌ها درست و لبه‌ها در جای خودشان برعکس)، به ۲۰ حرکت نیاز دارد.
دسامبر ۲۰۰۵ ۲۰ ۲۸ ۸ سیلویو رادو (Silviu Radu) ثابت کرد ۲۸ حرکت همواره کافی است.
آوریل ۲۰۰۶ ۲۰ ۲۷ ۷ سیلویو رادو، کران بالایش را به ۲۷ حرکت کاهش داد.
می ۲۰۰۷ ۲۰ ۲۶ ۶ دَن کانکِل (Dan Kunkle) و جین کوپرمن (Gene Cooperman) ثابت کردند ۲۶ حرکت کافی است.
مارس ۲۰۰۸ ۲۰ ۲۵ ۵ توماس روکیکی کران بالا را به ۲۵ بهبود داد.
آوریل ۲۰۰۸ ۲۰ ۲۳ ۳ توماس روکیکی و جان ولبورن (John Welborn) آن را به تنها ۲۳ حرکت کاهش دادند.
اوت ۲۰۰۸ ۲۰ ۲۲ ۲ توماس روکیکی و جان ولبورن در ادامه آن را به ۲۲ حرکت رساندند.
ژوئیه ۲۰۱۰ ۲۰ ۲۰ ۰ توماس روکیکی، هربرت کوکیمبا، مورلی دیویدسون (Morley Davidson) و جان دثریج (John Dethridge) ثابت کردند عدد خدا برای مکعب روبیک، دقیقاً ۲۰ است.

در اوت ۲۰۱۴ نیز توماس روکیکی و مورلی دیویدسون، ثابت کردند عدد خدا برای حرکت‌های ربع چرخشی، ۲۶ است[11] (حرکت ربع چرخشی، یعنی یکی از وجه‌های مکعب روبیک را ۹۰ درجه بچرخانیم، ۱۸۰ درجه چرخش خود شامل دو حرکت ربع چرخشی است و ۲۷۰ درجه چرخش نیز همان ۹۰ درجه چرخش از سوی دیگر است.).

جستارهای وابسته

منابع
  1. Paul Anthony Jones, Jedburgh Justice and Kentish Fire: The Origins of English in Ten Phrases and Expressions, Hachette UK, 2014 ISBN 1-4721-1622-4.
  2. See e.g. Rubik's Cubic Compendium by Ernö Rubik, Tamás Varga, Gerzson Kéri, György Marx, and Tamás Vekerdy (1987, Oxford University Press, ISBN 0-19-853202-4), p. 207: "...the Pyraminx is much simpler than the Magic Cube... Nicholas Hammond has shown that God's Algorithm is at most 21 moves (including the four trivial vertex moves). [More recently, three people have found God's Algorithm. The maximal number of moves is 15 (including the four vertex moves).]"
  3. Fildes، Jonathan (۲۰۱۰-۰۸-۱۱). «Speedy solution to Rubik's Cube» (به انگلیسی). دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
  4. «The Fifteen Puzzle can be solved in 43 "moves" | Domain of the Cube Forum». cubezzz.duckdns.org. دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
  5. «"Finding a shortest solution for the N × N extension of the 15-puzzle is intractable"» (PDF).
  6. «An optimal solution to the Towers of Hanoi Puzzle». web.archive.org. ۲۰۰۴-۰۶-۰۵. دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
  7. Richard E. Korf, "Finding optimal solutions to Rubik's Cube using pattern databases", Proc. Natl. Conf. on Artificial Intelligence (AAAI-97), Providence, Rhode Island, Jul 1997, pp. 700–705.
  8. «God's Number is 20». cube20.org. دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
  9. "God's Number - Looking for the optimal Rubik's Cube solution". ruwix.com. Retrieved 2019-05-30.
  10. «God's number is 20». kociemba.org. دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
  11. «God's Number is 26 in the Quarter Turn Metric». cube20.org. دریافت‌شده در ۲۰۱۹-۰۵-۳۰.
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.