ثابت اویلر–ماسکرونی
ثابت اویلر-ماسکرونی (با نام ثابت اویلر نیز شناخته میشود) یک ثابت ریاضی است که در آنالیز و نظریه اعداد بررسی میشود، این ثابت معمولاً با حرف یونانی گامای کوچک(γ) نشان داده میشود.
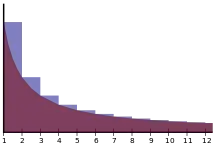
این ثابت به صورت حد تفاضل بین سری هارمونیک و لگاریتم طبیعی تعریف میشود:
در اینجا، تابع جزء صحیح را نشان میدهد.
مقدار عددی ثابت اویلر-ماسکرونی، تا ۵۰ رقم اعشار برابر است با:
| دودویی | ۰٫۱۰۰۱۰۰۱۱۱۱۰۰۰۱۰۰۰۱۱۰۰۱۱۱۱۱۱۰۰۰۱۱۰۱۱۱۱۱۰۱… |
| اعشاری | ۰٫۵۷۷۲۱۵۶۶۴۹۰۱۵۳۲۸۶۰۶۰۶۵۱۲۰۹۰۰۸۲۴۰۲۴۳۱۰۴۲۱… |
| بر مبنای شانزده | ۰٫۹۳C۴۶۷E۳۷DB۰C۷A۴D۱BE۳F۸۱۰۱۵۲CB۵۶A۱CECC۳A… |
| کسر مسلسل | [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, ...] (هنوز مشخص نیست که این کسر مسلسل متناهی یا نامتناهی دوره ای یا نامتناهی غیر دوره ای است. کسر مسلسل به روش علامتگذاری خطی نشان داده شدهاست) منبع: Sloane |
تاریخچه
لئونارد اویلر، ریاضیدان سوئیسی در مقاله ای با عنوان De Progressionibus harmonicis observationes (نمایهٔ Eneström 43) در سال ۱۷۳۴ اولین بار از این ثابت استفاده کرد. اویلر از علامت C و O برای این ثابت استفاده کرد. در سال ۱۷۹۰ ریاضیدان ایتالیایی، لورنزو ماسکرونی از نمادهای A و a برای آن استفاده کرد. علامت γ در هیچیک از نوشتههای اویلر و ماسکرونی دیده نمیشود و شاید بعداً به دلیل ارتباط آن با تابع گاما انتخاب شده باشد (Lagarias 2013). مثلاً، ریاضیدان آلمانی کارل آنتون برسشنایدر از علامت γ در سال ۱۸۳۵ استفاده کرد(Bretschneider 1837) و آگوستوس دمورگان از این علامت در یک کتاب درسی استفاده کردهاست. (De Morgan & 1836–1842)
ویژگیها
تابه حال جبری یا متعالی بودن عدد γ مشخص نشدهاست. در واقع، حتی گنگ بودن یا نبودن γ نیز معلوم نیست. پاپانیکولائو در سال ۱۹۹۷ با استفاده از تجزیه و تحلیل کسر مسلسل، نشان داد که اگر γ گنگ باشد، مخرج کسر غیرقابل قسم آن باید بیشتر از عدد 10244663 باشد.[1]
ارتباط با تابع گاما
γ به تابع دایگاما Ψ، و مشتق تابع گاما Γ مربوط است، مقدار هر دو تابع در نقطهٔ یک برابر است پس:
که این برابر با حد زیر است:
نتایج حدی بیشتر (Krämer 2005):
حد مربوط به تابع بتا است (که بر حسب توابع گاما بیان شدهاست)
کسر مسلسل
بسط کسر مسلسل γ به شکل روبه رو است [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, …] [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] OEIS: A002852، که الگوی آشکاری ندارد. ۴۷۵٬۰۰۶ مورد از اعداد الگوی بالا پیدا شدهاند،[1] و تعدادشان بینهایت است اگر و تنها اگر γ گنگ باشد.

منابع
- Haible, Bruno; Papanikolaou, Thomas (1998). Buhler, Joe P., ed. "Fast multiprecision evaluation of series of rational numbers". Algorithmic Number Theory. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 1423: 338–350. doi:10.1007/bfb0054873. ISBN 978-3-540-69113-6.
- Borwein, Jonathan M.; David M. Bradley; Richard E. Crandall (2000). "Computational Strategies for the Riemann Zeta Function" (PDF). Journal of Computational and Applied Mathematics. 121 (1–2): 11. Bibcode:2000JCoAM.121..247B. doi:10.1016/s0377-0427(00)00336-8. γ به عنوان مبالغی از توابع zeta ریمان استخراج میکند.
- Gerst, I. (1969). "Some series for Euler's constant". Amer. Math. Monthly. 76 (3): 237–275. doi:10.2307/2316370. JSTOR 2316370.
- Glaisher, James Whitbread Lee (1872). "On the history of Euler's constant". Messenger of Mathematics. 1: 25–30. JFM 03.0130.01.
- Gourdon, Xavier; Seba, P. (2002). "Collection of formulas for Euler's constant, γ".
- Gourdon , Xavier و Sebah , P. (2004) " ثابت اولر: γ " .
- Karatsuba, E. A. (1991). "Fast evaluation of transcendental functions". Probl. Inf. Transm. 27: 339–360.
- Karatsuba, E.A. (2000). "On the computation of the Euler constant γ". Journal of Numerical Algorithms. 24 (1–2): 83–97. doi:10.1023/A:1019137125281.
- Knuth, Donald (1997). The Art of Computer Programming, Vol. 1 (3rd ed.). Addison-Wesley. ISBN 0-201-89683-4. Knuth, Donald (1997). The Art of Computer Programming, Vol. 1 (3rd ed.). Addison-Wesley. ISBN 0-201-89683-4. Knuth, Donald (1997). The Art of Computer Programming, Vol. 1 (3rd ed.). Addison-Wesley. ISBN 0-201-89683-4.
- Lerch, M. (1897). "Expressions nouvelles de la constante d'Euler". Sitzungsberichte der Königlich Böhmischen Gesellschaft der Wissenschaften. 42: 5.
- Mascheroni, Lorenzo (1790), Adnotationes ad calculum integralem Euleri, in quibus nonnulla problemata ab Eulero proposita resolvuntur, Galeati, Ticini
- Lehmer, D. H. (1975). "Euler constants for arithmetical progressions" (PDF). Acta Arith. 27: 125–142. doi:10.4064/aa-27-1-125-142.
- Vacca, G. (1926). "Nuova serie per la costante di Eulero, C = 0,577...". Rendiconti, Accademia Nazionale dei Lincei, Roma, Classe di Scienze Fisiche". Matematiche e Naturali. 6 (3): 19–20.
پیوند به بیرون
- "Euler constant", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Euler–Mascheroni constant". MathWorld.
- Jonathan Sondow. بایگانیشده در ۱۰ دسامبر ۲۰۰۷ توسط Wayback Machine
- Fast Algorithms and the FEE Method, E.A. Karatsuba (2005)
- Further formulae which make use of the constant: Gourdon and Sebah (2004).