دوقطبی مغناطیسی
دوقطبی مغناطیسی (انگلیسی: Magnetic dipole) را میتوان حد یک حلقه جریان الکتریکی، یا یک جفت قطب مغناطیسی، وقتی اندازه آنها در حالی که گشتاور مغناطیسی ثابت میماند، بسیار کوچک میشود، در نظر گرفت.
اگرچه میتوان دوقطبی مغناطیسی را شبیه دوقطبی الکتریکی تصور کرد، اما این تصور چندان درست نیست، زیرا بر خلاف تکقطبی الکتریکی (بار مثبت و منفی)، تکقطبی مغناطیسی هرگز در طبیعت دیده نشدهاست. یک شکل از دوقطبی مغناطیسی، با یکی از بنیادیترین مفاهیم کوانتومی، یعنی اسپین ذرات بنیادی، مربوط است.
میدان مغناطیسی اطراف هر منبع مغناطیسی، بسیار شبیه میدان دوقطبی مغناطیسی، وقتی فاصله از منبع میدان افزایش مییابد، است.
میدان مغناطیسی بیرون گشتاور دوقطبی مغناطیسی
در فیزیک کلاسیک، میدان مغناطیسی دوقطبی حاصل از حلقه جریان الکتریکی یا دو قطب یک آهنربا، با فرض ثابت بودن گشتاور مغناطیسی m محاسبه میشود. برای حلقه جریان الکتریکی، پتانسیل برداری به راحتی محاسبه میشود. بیرون منبع میدان، این پتانسیل برابر است با:
۴πr2 مساحت کره با شعاع r است. چگالی شار مغناطیسی B از رابطه زیر بهدست میآید:
با روش دیگری میتوان ابتدا پتانسیل نردهای میدان دوقطبی یک جفت قطب آهنربا بهدست آورد:
سپس از آن، شدت میدان مغناطیسی (H) بهدست میآید:
میدان مغناطیسی، نسبت به محور گشتاور مغناطیسی، متقارن است.
میدان مغناطیسی درون دوقطبی
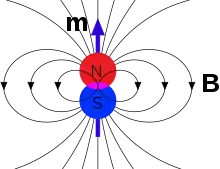
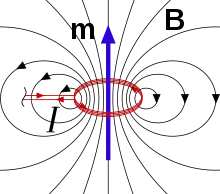
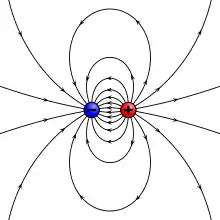
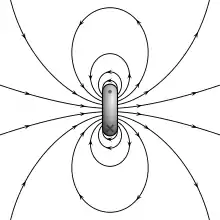
دو مدل دوقطبی مغناطیسی (مدل حلقه جریان و یک جفت قطب آهنربا) نتیجه یکسانی برای میدان مغناطیسی بیرون منبع مغناطیسی بهدست میدهند. با این حال میدان مغناطیسی درون دوقطبی مغناطیسی، متفاوت است. جهت میدان مغناطیسی درون قطبها در خلاف جهت گشتاور مغناطیسی (از بار منفی به بار مثبت) است درحالیکه اطراف حلقه جریان میدان همراستا با گشتاور دوقطبی است (شکل سمت چپ). البته اگر منبع مغناطیسی به حد یک نقطه کاهش یابد این محاسبات متفاوت خواهد بود. اگر یک دوقطبی مغناطیسی به وسیله یک حلقه حامل جریان خیلی خیلی کوچک شگل گیرد اما حاصلضرب جریان الکتریکی در مساحت حلقه ثابت نگه داشته شود میدان به صورت زیر محاسبه خواهد شد:
- .
در اینجا |n=x/|x بردار واحد و (δ(x تابع دلتای دیراک است. برخلاف اصطلاحات بخش قبل این میدان هم برای اطراف منبع و هم دور از آن صادق است. اگر یک دوقطبی مغناطیسی با در نظر گرفتن قطب شمال و جنوب شکل گیرد، با نزدیک کردن این قطبها به هم و با ثابت نگه داشتن حاصلضرب مقدار قطبها در فاصله میدان بطور تقریبی از رابطه زیر محاسبه میشود:
و شدت میدان از رابطه (B = μ0(H+M بدست میآید که در آن M مغناطش است:
نیروی بین دو دوقطبی مغناطیسی
نیرویی که یک دوقطبی با گشتاور m1 به دوقطبی دیگر با گشتاور m2 وارد میکند با بردار مکان r از روابط زیر محاسبه میشود[۳-۶]:
که در آن r فاصله بین دوقطبیهاست. جهت نیرو روی m1 در خلاف جهت بردار مکان است. گشتاور نیرو با رابطه زیر محاسبه میشود:
میدانهای دوقطبی منابع متناهی
پتانسیل مغناطیسی نردهای (ψ) یک منبع مغناطیسی متناهی در خارج از منبع را میتواند با گشتاورهای چند قطبی مغناطیسی نمایش داد. بطوری که گشتاور و پتانسیل مغناطیسی متناسب با چند قطبی با فاصله از منبع مغناطیسی با نرخ معینی کاهش مییابند. تک قطبی، دوقطبی و چهار قطبی مغناطیسی با فاصله از منبع به ترتیب با نرخ r-3, r-2 ,r-1 و به همین ترتیب برای چندقطبهای دیگر کاهش مییابند. در مراتب بالاتر پتانسیل با فاصله از منبع سریع تر افت میکند. با توجه به اینکه برای دوقطبی مغناطیسی کاهش پتانسیل با توان ۲ فاصله است بنابراین پتانسیل در فواصل بزرگتری از منبع مغناطیسی افت میکند.
منابع
- مشارکتکنندگان ویکیپدیا. «Magnetic dipole». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۴ ژانویه ۲۰۱۵.