میدان مغناطیسی

در الکترومغناطیس کلاسیک، میدان مغناطیسی، میدان به‌دست آمده از بار الکتریکی در حال حرکت می‌باشد. به سخن ساده‌تر، میدان مغناطیسی، حاصل تأثیر دو میدان الکتریکی (برای نمونه دو بار مثبت و منفی) بر روی هم است که به درست شدن یک میدان مغناطیسی می‌انجامد.

خطوط میدان مغناطیسی با براده‌های آهن نشان داده شده‌اند. تراوایی زیادی که هریک از براده‌های آهن دارند موجب ایجاد میدان مغناطیسی بزرگ‌تری در انتهای هر براده شده‌است. این باعث می‌شود هریک از براده‌ها یکدیگر را جذب کنند که یک مجموعه ممتدی به وجود می‌آید که شکل «خط» به خود می‌گیرد. انتظار نمی‌رود که این «خط»ها همان خطوط میدان مغناطیسی آهنربا باشند زیرا میدان مغناطیسی براده‌ها مقداری در میدان آهنربا تأثیر می‌گذارد.

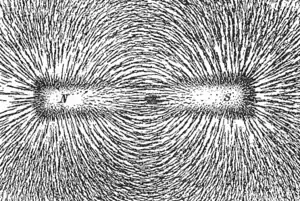
میدان مغناطیسی از تک بارها، سیم‌های حامل جریان، جهت‌گیری دوقطبی‌های مغناطیسی (آهنرباهای دایمی)، جریان سیال رسانا (میدان مغناطیسی زمین) ایجاد می‌شوند.

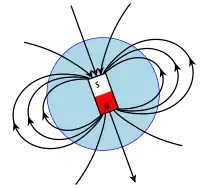
نقشه ساده‌ای از میدان مغناطیسی کره زمین که منبع میدان مغناطیسی زمین را به صورت یک آهنربا نشان می‌دهد. قطب شمال زمین در نزدیکی بالای تصویر و قطب جنوب نزدیک پایین آن است. توجه کنید که قطب جنوب آهنربا در اعماق داخل زمین در زیر قطب جنوب مغناطیسی آن است. میدان مغناطیسی زمین حاصل عبور جریان دائم الکتریکی در هسته مایع خارجی آن است

در الکترودینامیکِ نسبیتی، تفاوتی میان میدان الکتریکی و میدان مغناطیسی وجود ندارد و میدان الکترومغناطیسی، اثر بار الکتریکی در اطراف آن تعریف می‌شود. چون حرکت، کاملاً نسبی در نظر گرفته می‌شود و نمی‌توان بین بار ثابت و بار متحرک تفاوتی قایل شد (متحرک بودن یا ثابت بودن برای بیننده‌های گوناگون تفاوت می‌کند). نیروی حاصل از این میدان را نیروی لورنتس می‌خوانند.

به دیگر سخن، میدان مغناطیسی میدانی است که توسط یک جسم مغناطیسی یا ذرات یا با تغییر میدان الکتریکی تولید شده‌است[1] و توسط نیرویی که روی دیگر مواد مغناطیسی یا حرکت بار الکتریکی اعمال می‌شود شناسایی می‌شود. میدان مغناطیسی در هر نقطهٔ داده شده توسط هر دو پارامتر جهت و شدت (یا مقاومت) مشخص می‌شود که به عنوان یک میدان برداری شناخته می‌شود.[1] اشیایی که خود میدان مغناطیسی تولید می‌کنند آهن‌ربا نامیده می‌شوند. آهن‌رباها توسط نیروها و گشتاورهایی که توسط میدان‌های مغناطیسی تولید می‌کنند بر یکدیگر تأثیر می‌گذارند. آهن‌ربا معمولاً خود را به سوی میدان مغناطیسی موضعی تراز می‌کند. قطب‌نماها از این اثر برای اندازه‌گیری جهت میدان مغناطیسی موضعی، تولید شده توسط زمین استفاده می‌کنند. ریاضیات پیچیده که میدان مغناطیسی یک چیز را نشان می‌دهد با بکارگیری خطوط میدان مغناطیسی نشان داده می‌شوند. این خطوط صرفاً یک مفهوم ریاضی است و به صورت فیزیکی وجود ندارد. با این حال، برخی پدیده‌های فیزیکی از قبیل تراز شدن براده‌های آهن در یک میدان مغناطیسی، به مانند خطوط در یک الگوی مشابه با خطوط فرضی میدان مغناطیسی از جسم را می‌سازد. جهت خطوط میدان مغناطیسی که تراز دل‌خواه برای برادهٔ آهنی که بر روی کاغذی که بر روی یک نوار آهن‌ربا قرار دارد، پاشیده شده‌است. نشان می‌دهد. ربایش متقابل قطب مخالف براده آهن به تشکیل خوشه‌های دراز از براده در امتداد خطوط میدان انجامیده‌است.

قاعده دست راست

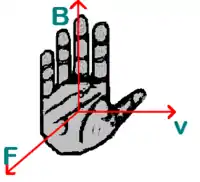
جریان الکتریسیته و انتقال شار الکتریکی میدان مغناطیسی (مِگناتیک) می‌سازد. حتی میدان مغناطیسی از یک ماده مغناطیسی را می‌توان به عنوان مدل حرکت شار الکتریکی الگو گرفت.[2] میدان مغناطیسی نیز بر روی حرکت شار الکتریکی نیرو وارد می‌کند. میدان‌های مغناطیسی در داخل و با توجه به مواد مغناطیسی می‌تواند کاملاً پیچیده باشد. میدان مغناطیسی با مواد دیگر اثر متقابلی دارد، بنابراین میدان مغناطیسی متقابلی با مواد دیگر ایجاد می‌کند. شرح میدان مغناطیسی در داخل آهن‌ربا شامل دو رشته جداگانه است که می‌تواند هر دو به نام میدان مغناطیسی، میدان مغناطیسی B و میدان مغناطیسی H نامیده شود. این‌ها توسط یک میدان سوم که توصیف حالت مغناطیسی مواد مغناطیسی در درون آن‌هاست، که مغناطیس‌کنندگی نامیده می‌شود تعریف می‌شود. انرژی نیازین برای ساخت میدان مغناطیسی می‌تواند زمانی که میدان از بین می‌رود اصلاح شود؛ و این انرژی می‌تواند، به عنوان «ذخیره شده» در میدان مغناطیسی در نظر گرفته شود. انرژی ذخیره شده در مواد مغناطیسی به مقادیر B و H بستگی دارد. میدان الکتریکی میدانی است که توسط شار الکتریکی ایجاد شده‌است و این میدان‌ها به‌طور تنگاتنگی به میدان‌های مغناطیسی مربوط می‌شوند؛ تغییر در میدان مغناطیسی میدان الکتریکی و تغییر در میدان الکتریکی میدان مغناطیسی تولید می‌کند. (رجوع کنید به الکترومغناطیس) ارتباط کامل بین میدان‌های الکتریکی و مغناطیسی و جریان و شار که آن‌ها را ایجاد می‌کنند، توسط مجموعه‌ای از معادلات ماکسول توصیف می‌شوند. با در نظرگرفتن این ارتباط خاص، میدان‌های الکتریکی و مغناطیسی دو زمینه پیوسته از یک موضوع یکسان، به نام میدان الکترومغناطیسی هستند. یک میدان الکتریکی خالص، در یک چارچوب مرجع، به عنوان ترکیبی از هر دو میدان الکتریکی و میدان مغناطیسی که در یک چارچوب مرجع حرکت می‌کند، دیده می‌شود. در فیزیک کوانتومی، میدان مغناطیسی خالص (و الکتریکی) را توسط اثرات ناشی از فوتون‌های مجازی می‌توان دریافت و در زبان مدل استاندارد، نیروی الکترومغناطیسی در تمام مظاهر توسط فوتون واقع می‌شود. در بیشتر موارد این شرح میکروسکوپی نیاز نمی‌باشد چرا که نظریهٔ کلاسیک ساده، قانع‌کننده است؛ تفاوت تحت میدان با انرژی پایین‌تر در بیشتر شرایط قابل چشم‌پوشی است.

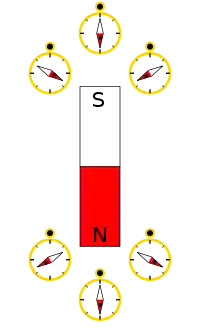
جهت میدان مغناطیسی در نزدیکی قطب‌های آهنربا با قرار دادن قطب‌نما در نزدیک آن مشخص می‌شود. همان‌طور که دیده می‌شود میدان مغناطیسی به سمت قطب S آهنربا و به سمت خارج از قطب N آن است

میدان‌های مغناطیسی در جوامع کهن و نوین استفاده‌های بسیار داشته‌است. زمین میدان مغناطیسی خود را می‌سازد؛ که در جهت‌یابی ای که توسط قطب شمال قطب‌نما که به سمت قطب جنوب میدان مغناطیسی زمین منحرف شده‌است، بسیار حایز اهمیت است. از چرخش میدان مغناطیسی در موتور الکتریکی و ژنراتور بهره گرفته شده‌است که باعث تولید برق میشود. نیروهای مغناطیسی ارائه دهندهٔ اطلاعاتی در مورد حرکت شار از طریق اثر هال هستند. تداخل و درهم شدن میدان‌های مغناطیسی در دستگاه‌های الکتریک مانند ترانسفورماتورها در نظم حوزه‌های مغناطیسی مطالعه شده‌اند. مطالعه میدان مغناطیسی به عنوان یک موضوع جدا از آهن‌ربا در سده ۱۳ م. هنگامی که پترو پرگرینوس د ماریکور میدان مغناطیسی آهنربای کروی (گویی) را مطالعه کرد و انگاشت که زمین خود یک آهنربا است آغازید. تمایز مدرن میان میدان‌های B و H در سده ۱۹ کشف شد. رابطه میان میدان‌های الکتریکی و مغناطیسی در مجموعه‌ای از معادلات ماکسول در نیمه دوم سده ۱۹ میلادی کشف شد؛ و مفهوم الکترومغناطیس زاده شد. روندی که در پشت معادلات ماکسول بود در نیمه نخست سده ۲۰ آشکار شد، هنگامی که ارتباط ویژه آن‌ها نشان داده شد. شرح کاملی از الکترومغناطیس، الکترودینامیک کوانتومی یا QED نامیده می‌شود، که شامل مکانیک کوانتومی که در میانه‌های سده ۲۰ پی برده شده است.

B و H

در میدان مغناطیسی برای دو میدان برداری مختلف استفاده می‌شود، که میدان‌های B و H نامیده می‌شوند توجه[3] بسیاری از نام‌های جایگزین برای هر دو وجود دارد) نگاه کنید به جداول زیر) برای اجتناب از اشتباه، در این مقاله از میدان B و میدان H استفاده کرده‌است. در هر مورد که هر دوی آن‌ها استفاده شده‌اند از میدان مغناطیسی نام برده شده‌است.

Alternative names for B
name	used by
magnetic flux density	electrical engineers
magnetic induction	applied mathematicians electronics engineers
magnetic field	physicists

Alternative names for H
name	used by
magnetic field intensity	electrical engineers
magnetic field strength	electronics engineers
auxiliary magnetic field	applied mathematicians
magnetizing field	physicists

خارج از مواد، میدان‌های B و H غیرقابل تشخیص هستند. (آن‌ها تنها در واحدهای خود و مقدار، متفاوتند و در تغییرات زمانی و مکانی تفاوتی ندارند) تنها در داخل ماده‌ای که تفاوت مهم است. میدان B به جریان بستگی دارد (هم ماکروسکوپی وهم میکروسکوپی مانند حرکت الکترون به دور هسته آن). در حالی که میدان H به جریان‌های ماکروسکوپی و برداری که به پدیدهٔ شار مغناطیسی بسیار نزدیک است، بستگی دارد.

میدان B را می‌توان در بسیاری جهات مشابه، بر اساس اثرات آن بر روی محیط اطراف آن تعریف کرد. به عنوان مثال، یک ذره با بار الکتریکی q و حرکت در میدان B با سرعت v، نیرویی به نام F ایجاد می‌کند که نیروی لورنتس نامیده می‌شود. (پایین را ببینید) در واحد SI، نیروی لورنتس برابر است با: $\mathbf {F} =q\left(\mathbf {v} \times \mathbf {B} \right)$ که در آن × بردار ضرب خارجی است. یک تعریف متناوب کاری از میدان B را می‌توان از لحاظ گشتاور دو قطبی مغناطیسی در میدان B ارائه داد:

{\boldsymbol {\tau }}=\mathbf {m_{m}} \times \mathbf {B}

برای دو قطبی مغناطیسی لحظه‌ای m (در آمپر متر مربع). میدان B در واحد SI تسلا و در واحد cgs گاوس نامیده می‌شود. (۱ تسلا = ۱۰۰۰۰ گاوس). در واحد SI تسلا برابر است با: (کولن × متر) / (نیوتن × ثانیه) همان‌طور که از قسمت مغناطیسی قانون نیروی لورنتس می‌توان دید: F_mag = (qv × B). H به عنوان اصلاحی برای B به علت میدان مغناطیسی تولید شده توسط مواد واسطه خواهد بود، به‌طوری‌که (در SI):

\mathbf {H} \ \equiv \ {\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} ,

که در آن M مغناطیسی شدن ماده و μ₀ نفوذپذیری مغناطیسی در فضای خالی است (یا پایداری مغناطیسی).[1] میدان H با یکای آمپر بر متر در SI.(A/m) و اورستد (Oe) در cgs اندازه‌گیری می‌شود. در موادی که M متناسب با B است، رابطه بین B و H را می‌توان به فرم ساده‌تر نوشت: H = B/μ که در آن μ پارامتر وابسته به مواد به نام نفوذپذیری است. در فضای خالی، هیچ مغناطیسی وجود ندارد M به‌طوری‌که H = B/μ هر چند، برای بسیاری از مواد، هیچ رابطهٔ ساده‌ای بین B و M وجود ندارد به عنوان مثال، مواد فِرّومغناطیسی و ابررساناها خاصیت مغناطیسی شدنی دارند که یک تابع چند ارزشی از B مربوط به پسماند مغناطیسی است.

نیروی الکترومغناطیسی سیم حامل جریان

اگر سیمی که حامل جریان الکتریکی است در یک میدان مغناطیسی قرار گیرد نیرویی بر این سیم وارد می‌شود. این نیرو با طول سیم (L) و چگالی شار مغناطیسی (B) رابطه مستقیم دارد. این رابطه به‌صورت: $F=L\,I\,B\,\sin \alpha$ نشان داده می‌شود؛ بنابراین رابطه: اگر سیم در راستای میدان مغناطیسی قرار گیرد نیروی وارد بر آن صفر است زیرا α=۰° Sin 0°=۰ یا α=۱۸۰° Sin 180°=۰ در نتیجه ۰=F است. اگر سیم به صورت عمود قرار گیرد نیروی وارد بر آن حد اکثر است. اگر سیم شکل نامنظمی داشته باشد آن را به دو مؤلفهٔ (عمودی و افقی) تقسیم می‌کنیم و از مؤلفهٔ عمودی استفاده می‌کنیم. برای پیدا کردن جهت میدان بر اساس قاعده دست راست عمل می‌شود.

میدان مغناطیسی اطراف سیم راست

اگر از سیم راستی، جریان عبور کند، اطراف آن سیم، میدان مغناطیسی ایجاد می‌شود.

میدان مغناطیسی داخل سیم لوله حامل جریان

میدان مغناطیسی داخل سیم لوله به تعداد پیچش سیم در واحد متر دور هسته‌ای آهنی که قرار گرفتن آن موجب تقویت میدان که با B نشان می‌دهند خواهند شد، علاوه بر آن به جریان عبوری نیز بستگی دارد طوری‌که هرچه جریان بزرگتر باشد، میدان تولید شده بزرگتر خواهد بود، و علاوه بر آن‌ها به سطح تراوا الکترومغناطیسی نیز بستگی دارد.

میدان مغناطیسی و آهن‌ربای دائم

آهنرباهای دائم اشیائی هستند که میدان‌های مغناطیسی مداوم خود را تولید می‌کنند. همه آهنرباهای دائم دو قطب شمال و جنوب دارند. آن‌ها از مواد فِرّومغناطیسی مانند آهن و نیکل که مغناطیسی شده‌اند ساخته شده‌اند.

شعاع‌های الکترون در یک دایره حرکت می‌کنند. نور نتیجه برانگیختگی اتم‌های گاز در لامپ است

متأسفانه مفهوم قطب‌های 'شار مغناطیسی' با دقت آنچه در داخل آهنربا اتفاق می‌افتد را منعکس نمی‌کند (نگاه کنید به فرو مغناطیسی شدن)؛ شار مغناطیسی وجود ندارد. به عنوان مثال، بر خلاف شار الکتریکی، آهن‌رباها نمی‌تواند قطب‌های جداگانه‌ای در شمال و جنوب قطب داشته باشند؛ همه آهنرباها جفت شمال و جنوب دارند. علاوه بر این، آهنربای کوچک داخل آهنربا بزرگتر در جهت مخالف به آنچه از میدان H انتظار می‌رود پیچیده می‌شود. شرح فیزیکی صحیح تر مغناطیسی شدن شامل حلقه‌های اتمی جریان که در سراسر آهنربا توزیع شده‌است، می‌باشد.[4] در این مدل، یک آهنربا از بسیاری از آهنرباهای کوچک، به نام دو قطبی مغناطیسی که هر کدام یک جفت قطب شمال و جنوب مربوط به جریان الکتریکی دارند، تشکیل شده‌است. هنگامی که در ترکیب آن‌ها به صورت یک آهنربا که قدرت مغناطیسی دارد m. که برای راحتی محاسبات ریاضی است، همچنین با توجه به جهت متناظر با جهت‌گیری‌های میدان مغناطیسی آن را تعریف می‌کنند. برای آهنرباهای ساده، m در جهت خط از جنوب تا قطب شمال آهن‌ربا کشیده شده‌است. نیروی گرانش بین دو آهنربا کاملاً پیچیده و وابسته به قدرت و جهت‌گیری هر دو آهنربا و وابسته به مسافت و و جهت آهنرباهای متصل به یکدیگر. است. نیرو حساس به چرخش از آهن‌ربا به علت گشتاور مغناطیسی است. نیروی هر آهنربا در هر لحظه بستگی به خود آهنربا و میدان مغناطیسی B[3] از سوی دیگر، دارد. میدان B یک آهنربا ی کوچک بسیار پیچیده‌تر است. در ریاضیات، نیرو در یک آهنربای که یک مغناطیسی شدن لحظه‌ای m، مربوط به میدان مغناطیسی B دارد برابر است با:[5]

\mathbf {F} =\mathbf {\nabla } \left(\mathbf {m} \cdot \mathbf {B} \right),

که در آن∇ شیب تغییرات مقدار m B. در هر واحد از فاصله و جهت است که افزایش حداکثر m.B را محصول است (نقطه معادله زیر را ایجاد می‌کند. ضرب داخلی:(m · B = mBcos(θکه در آن m و B نشان از اندازه بردارهای m و B است و θ زاویه بین آن‌ها است) این معادله صرفاً فقط برای آهنرباهای صفر اندازه معتبر است، اما اغلب می‌توان به عنوان تقریبی برای آهن‌رباهای نه چندان بزرگ استفاده کرد. نیروی مغناطیسی در آهنرباهای بزرگتر از تقسیم آن‌ها به مناطق کوچکتر با m مشخص و سپس جمعبندی نیروهای در هر یک از این مناطق تعیین می‌شود.

گشتاور در آهنربا مربوط به میدان B

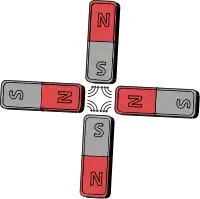
طرحواره‌ای از آهنربای چهار قطبی. چهار نوک ثابت قطب‌های آهنربا هستند که دو تای آن‌ها با قطب N و دو تا با قطب S مخالفت می‌کنند

گشتاور در آهنربا مربوط به میدان مغناطیسی خارجی می‌تواند با قرار دادن دو آهنربا در نزدیکی یکدیگر در حالی که یکی از آن‌ها شروع به چرخش می‌کنند مشاهده می‌شود. گشتاور مغناطیسی برای به کار انداختن موتورهای ساده الکتریکی استفاده می‌شود. در یک طرح موتور ساده، آهنربا بر روی یک شفت که آزادانه چرخش می‌کند ثابت شده‌است که تحت میدان مغناطیسی ردیفی از الکترومغناطیسی‌ها قرار دارد.. با سوئیچینگ مداوم جریان الکتریکی از هر کدام از آهنرباهای الکتریکی، با توجه به تغییر میدان مغناطیسی آن‌ها، مانند قطب شمال و جنوب کنار روتور، گشتاور حاصل به محور منتقل می‌شود. میدان مغناطیسی دوار را مشاهده کنید. گشتاور مغناطیسی τ تمایل دارد قطب مغناطیسی با خطوط میدان B در یک امتداد قرار دهد (تا زمانی که m در جهت قطب‌های مغناطیسی است می‌توان گفت m تمایل دارد با B در یک امتداد قرار بگیرد) به همین دلیل است سوزن مغناطیسی قطب‌نما به سمت قطب شمال زمین منحرف می‌شود. با این تعریف، جهت میدان محلی مغناطیسی زمین جهتی است که در آن قطب شمال قطب‌نما (یا هر آهنربایی) تمایل به آن نقطه دارد. به‌طور ریاضی وار، گشتاور τ آهنربای کوچک متناسب با هر دوی میدان B اعمال شده مغناطیسی شدن آهنربا m می‌باشد:

{\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B} ,\,

که در آن × نشان دهندهٔ بردار ضرب خارجی است. در نظر داشته باشید که این معادله شامل تمام اطلاعات کیفی شامل بالامی باشد. هیچ گشتاور مغناطیسی در صورتی که m در امتداد B قرار بگیرد، وجود ندارد (مفهوم ضرب خارجی) علاوه بر این، در تمامی جهت‌ها گشتاوری که آن‌ها را به جهت B متمایل می‌کند احساس می‌شود.

کاربرد در پژوهش‌ها

در ژانویه ۲۰۱۳ فیزیکدانان ذرات یک گاز کوانتومی بر پایه پتاسیم ساختند. این گاز هنگامی که تحت تأثیر لیزر و میدان مغناطیسی قرار می‌گیرد به دماهای منفی می‌رسد. در این دمای ترمودینامیکی، ماده شروع به بروز دادن خواص ناشناخته پیشین می‌کند.[6][7]

جستارهای وابسته

منابع

مبانی نظریه الکترومغناطیس، ریتس و میلفورد

آشنایی با حساب تنسوری و نسبیت، درک لاودن

Durney, Carl H. and Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw Hill Financial. ISBN 0-07-018388-0.
Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 0-13-948746-8. OCLC 221993786.
Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.
Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. OCLC 224523909.
Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8. OCLC 51095685.
"Quantum gas temperature drops below absolute zero". Wired. 4 January 2013. Archived from the original on 24 January 2013. Retrieved 5 February 2013.
"Quantum gas goes below absolute zero". Nature. 3 January 2013. Retrieved 5 February 2013.

Furlani, Edward P. (2001). Permanent Magnet and Electromechanical Devices: Materials, Analysis and Applications. Academic Press Series in Electromagnetism. ISBN 0-12-269951-3. OCLC 162129430.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Durney,_Carl_H._and_Johnson,_Curtis_C._1969-1] Durney, Carl H. and Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw Hill Financial. ISBN 0-07-018388-0.

[2] Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 0-13-948746-8. OCLC 221993786.

[Griffiths,_David_J._1999-3] Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.

[4] Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. OCLC 224523909.

[5] Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8. OCLC 51095685.

[6] "Quantum gas temperature drops below absolute zero". Wired. 4 January 2013. Archived from the original on 24 January 2013. Retrieved 5 February 2013.

[7] "Quantum gas goes below absolute zero". Nature. 3 January 2013. Retrieved 5 February 2013.

موتورهای الکتریکی
AC - جریان متناوب DC - جریان مستقیم PM - آهنربا SC - خود-جابه‌جاگر
انواع اساسی	موتور جریان متناوب موتور جریان مستقیم
موتورهای جریان مستقیم	موتور هموپلار Electrically-excited field or PM field brushed DC موتور تک‌قطبی
AC SC مکانیکی کموتاتور	Repulsion موتور یونیورسال
AC SC الکترونیکی کموتاتور	موتور بدون جاروبک دی‌سی Switched reluctance (SRM)
موتور القایی جریان متناوب	موتور قطب‌چاکدار موتور دالاندر موتور القایی Wound-rotor (WRIM) موتور القایی خطی
موتور سنکرون جریان متناوب	موتور سنکرون موتور بدون جاروبک دی‌سی موتور رلوکتانسی موتور سنکرون
ماشین‌های مغناطیسی ویژه	دو سو تغذیه خطی سروموتور موتور پله‌ای موتور کششی
غیرمغناطیسی	موتور الکتروستاتیک Piezoelectric Ultrasonic
نوع محفظه	محفظه هرمس TEFC
اجزا و یراق	آرمیچر Braking chopper جاروبک کموتاتور DC injection braking میدان کویل روتور حلقه لغزش ایستانه سیم‌پیچ
کنترل‌کننده موتور	مبدل AC/AC Amplidyne درایو سرعت قابل تنظیم سیکلوکنورتور کنترل مستقیم گشتاور (DTC) متادین کنترل‌کننده موتور راه‌انداز نرم استارت معکوس‌گر توان محرکه تریستوری محرکه فرکانس‌متغیر کنترل برداری کنترل‌کننده ولتاژ Ward Leonard control
تاریخچه، کاربرد آموزشی و تحقیقاتی	نوار زمانی موتور الکتریکی موتور بلبرینگی چرخ بارلو Lynch motor Mendocino motor Mouse mill motor
آزمایشی	تفنگ پیچه‌ای Railgun Superconducting machine
موضوعات مرتبط	آزمایش رتور قفل‌شده دیاگرام دایره‌ای Closed-loop control الکترومغناطیس آزمایش مدار باز کنترل‌کننده حلقه باز توان وزنی مخصوص Torque and speed of a DC motor توان الکتریکی دو فاز
افراد	فرانسوا آراگو Baily Barlow جوزپه دومنیکو بوتو Cook Davenport Davidson میکائل دولی‌وو-دبرولسکی مایکل فارادی گالیله فراری Froment زنوب گرامه جوزف هانری موریتس فن یاکوبی انیوس جدلیک هاینریش لنز جیمز کلرک ماکسول هانس کریستین اورستد رابرت اچ. پارک Pixii Saxton ورنر فون زیمنس فرانک سپری چارلز پرتیوس استینمتز Stimpson ویلیام استورجن نیکولا تسلا
جستارهای وابسته	مولد هم‌زمان ژنراتور الکتریکی Inchworm motor
SI electromagnetism units	C - ظرفیت خازنی Q - بار الکتریکی G, B, Y - ادمیتانس κ, γ, σ - Conductivity (S/m) I - جریان الکتریکی D - میدان جابجایی الکتریکی E - میدان الکتریکی Φ_E - شار الکتریکی χ_e - ضریب حساسیت الکتریکی U, ΔV, Δφ; E - نیروی محرک الکتریکی L, M - ضریب خودالقایی H - میدان مغناطیسی strength Φ - شار مغناطیسی B - میدان مغناطیسی χ - پذیرفتاری مغناطیسی μ - تراوایی مغناطیسی ε - گذردهی (فیزیک) P - توان الکتریکی R, X, Z - امپدانس الکتریکی ρ - Resistivity (Ω·m)