امپدانس الکتریکی
| مقالات در مورد |
| الکترومغناطیس |
|---|
 |
|

- امپدانس الکتریکی، مفهوم کلیتر مقاومت الکتریکی، و مقدار مقاومتی است که تحت یک اختلاف پتانسیل متناوب در برابر جریان الکتریکی متناوب ظاهر میشود. مقدار امپدانس، عددی حقیقی یا مختلط است که بنابر قانون اهم از نسبت ولتاژ به جریان به دست میآید. امپدانس با نماد نمایش داده میشود.
- در مداری که تحت ولتاژ و جریان متناوب قرار دارد، مقادیر ولتاژ و جریان تحت تبدیل فازبردار به صورت مختلط نمایش داده میشوند و در نتیجه امپدانس، عددی مختلط خواهد بود. بنابراین در یک مدار با ولتاژهای مستقیم، امپدانس عددی حقیقی خواهد بود.
- امپدانس الکتریکی اندازه گیری مقاومتی است که مدار هنگام اعمال ولتاژ به جریان می دهد. اصطلاح امپدانس مختلط ممکن است به صورت متناوب استفاده شود. از نظر کمی ، امپدانس یک عنصر مدار دو ترمیناله نسبت نمایش مختلط یک ولتاژ سینوسی بین پایانه های آن به نمایش مختلط جریان جاری در آن است. [1] به طور کلی ، امپدانس به فرکانس ولتاژ سینوسی بستگی دارد. امپدانس مفهوم مقاومت در مدارهای AC را توسعه می دهد ، و برخلاف مقاومت ، که فقط دارای اندازه است، دارای اندازه و فاز می باشد. هنگامی که یک مدار با جریان مستقیم (DC) هدایت می شود ، هیچ تمایزی بین مقاومت و امپدانس وجود ندارد. و مقاومت را می توان به عنوان امپدانس با زاویه فاز صفر تصور کرد. مفهوم امپدانس برای انجام تجزیه و تحلیل AC شبکه های الکتریکی مفید است ، زیرا اجازه می دهد رابطه بین ولتاژ سینوسی و جریان مربوطه را با یک قانون ساده خطی بیان نمود. در شبکه های با پورت های متعدد ، تعریف دو ترمینالی برای امپدانس ناکافی است ، اما ولتاژهای مختلط در پورت ها و جریان های جریان یافته از طریق آنها هنوز هم به صورت خطی با ماتریس امپدانس مرتبط هستند. [2]
امپدانس یک عدد مختلط، با همان واحدهای مقاومت است ، که واحد SI آن اهم (Ω) است. نماد آن معمولاً Z است و ممکن است با نوشتن بزرگی و فاز آن به صورت | Z | ∠θ نشان داده شود. با این حال ، نمایش عدد مختلط کارتزینی اغلب برای اهداف تجزیه و تحلیل مدار قدرتمندتر است. متقابل امپدانس، ادمیتانس است ، که واحد SI آن زیمنس است ، که به صورت رسمی تر mho اطلاق می شود. ابزارهایی که برای اندازه گیری امپدانس الکتریکی مورد استفاده قرار می گیرند ، آنالایزر امپدانس نامیده می شوند. اصطلاح امپدانس توسط الیور هویزاید در ژوئیه 1886 ابداع شد. [3] [4] آرتور کنلی اولین کسی بود که در سال 1893 با اعداد مختلط امپدانس را نشان داد. [5] علاوه بر مقاومت همانطور که در مدارهای DC دیده می شود ، امپدانس در مدارهای AC شامل اثر القایی ولتاژ در رساناها توسط میدانهای مغناطیسی (اندوکتانس) ، و ذخیره الکترواستاتیک بار ناشی از ولتاژهای بین رساناها (خازن) است. امپدانس ناشی از این دو اثر در مجموع به عنوان مقاومت القایی (ری اکتانس) شناخته می شود و قسمت موهومی امپدانس مختلط را تشکیل می دهد در حالی که مقاومت قسمت حقیقی آن را تشکیل می دهد. امپدانس به عنوان نسبت دامنه فرکانس ولتاژ به جریان تعریف می شود. [6] به عبارت دیگر ، این نسبت ولتاژ به جریان برای یک نمایی مختلط منفرد در یک فرکانس خاص ω است. برای یک جریان سینوسی یا ولتاژ ورودی، شکل قطبی امپدانس مختلط، مرتبط با دامنه و فاز ولتاژ و جریان است. به خصوص: - بزرگی امپدانس مختلط، نسبت دامنه ولتاژ به دامنه جریان است. - فاز امپدانس مختلط، شیفت فازی است که توسط آن جریان ولتاژ را عقب می اندازد.
امپدانس مختلط
امپدانس یک مدار دو ترمیناله به صورت یک کمیت مختلط Z نمایش داده می شود. شکل قطبی به صورت قراردادی هم اندازه و هم فاز را به صورت زیر در بر می گیرد:
که در آن بیانگر نسبت تفاضل دامنه ولتاژ به دامنه جریان است و جمله arg (Z) (معمولا با نماد q نشان داده می شود) تفاضل فاز بین ولتاژ و جریان را می دهد. j واحد موهومی است که به جای i به منظور جلوگیری از سردر گمی ، به کار گرفته می شود.
در نمایش کارتزین، امپدانس به صورت زیر تعریف می شود:
جائیکه بخش حقیقی آن، مقاومت R و قسمت موهومی آن همان رکتانس است.
در شرایطی که تفریق یا تجمیع امپدانس لازم باشد ، فرم دکارتی راحت تر است. اما وقتی نیاز به ضرب یا تقسیم باشد، اگر از فرم قطبی استفاده شود ، محاسبه ساده تر می شود. در طی یک محاسبه مداری ، مانند یافتن امپدانس کل دو امپدانس به طور موازی ، ممکن است در مسیر محاسبه نیاز به تبدیل چندین بار بین فرم نوشتاری داشته باشد. تبدیل بین فرمها از قوانین عادی تبدیل اعداد مختلط پیروی می کند.
قانون اُهم
بر طبق این قانون هرگاه دمای یک جسم (مثلا یک رسانا) ثابت باشد نسبت اختلاف پتانسیل دو سر جسم به شدت جریانی که از ان عبور میکند مقدار ثابتی است که این نسبت را مقاومت الکتریک جسم مینامیم و از رابطهٔ R=V/I تبعیت میکند که در ان V یا ولتاژ برحسب ولت و I یا جریان بر حسب آمپر و R بر حسب اهم است. تقریباً تمام مقاومتهای خطی از رابطهٔ بالا پیروی میکنند.
جریان و ولتاژ مرکب

مثالی از راه حلی خلاقانه
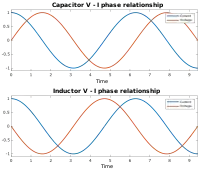
مقاومت و رآکتانس
مقاومت رسانا
معمولاً مواد را از جنبهٔ رسانایی به سه دسته کلی ۱-مواد رسانا :موادی که حرارت و جریان الکتریکی را به خوبی از خود عبور میدهند مانند فلزاتی از قبیل (طلا، مس، آهن و...) رسانایی این مواد تحت تأثیر دما دستخوش تغییراتی میشود و با بالا رفتن دما مقاومت آنها زیاد میشود و با پایین آمدن دما مقاومتهای آنها نیز پایین می اید که حتی در دماهای خیلی پایین حالت ابر رسانا نیز رخ میدهد. معمولاً در دمای ثابت مقاومت را با توجه به سطح (مساحت) مقطع جسم، طول جسم و خصوصیات فیزیکی جسم (جنس جسم و....) و از ربطه R=ρ(L/A)اندازهگیری میکنند که در ان R یا مقاومت بر حسب اهم، L یا طول رسانا برحسب متر و A مساحت سطح مقطع بر حسب متر -مربع میباشد و ρ نیز رسانایی ویژه رسانا میباشد که به خصوصیات ذاتی ماده بر میگردد و در آزمایشگاه اندازهگیری میشود. لازم به توضیح بسیار مهم است که مقاومت به اختلاف پتانسیل و جریان عبوری وابسته نیست بلکه جنس و شکل ماده بستگی دارد که از رابطه بالا همین نتیجه قابل استنباط میباشد.
۲- مواد نیمه رسانا: این دسته از مواد دارای هدایت الکتریکی کمتری بوده ولی ویژگی مطرح آن قابل کنترل بودن هدایت آن است. مواد نیمه رسانا مانند سیلیسیوم (سیلیکن) و ژرمانیوم را میتوان نام برد. تغییرات رسانایی مواد نیمه رسانا تابع عواملی چون تحریک نوری و تغییرات دما و خلوص آتها است چراکه مواد نیمه رسانا رسانایی جالبی ندارند ولی بعد از افزایش مقداری ناخالصی رسانایی آنها بشدت افزایش مییابد از مواد نیمه رسانا در ساختمان دیودها استفاده میشود.
۳- مواد عایق که از نظر هدایت الکتریکی در ولتاژهای پایین بهره مناسبی ندارند.
رآکتانس
خازن و سلف در هنگام عبور جریان از آنها دارای مقادیری مقاومت موهومی میشوند که به آنها راکتانس میگویند و معمولاً آن را با X نشان میدهند
ترکیب امپدانسها
امپدانس خازن از رابطهٔ jXc- بدست می آید که در ان Xc=۱/ωC و C ظرفیت خازن است و به آن راکتانس خازن میگویند. امپدانس خازن از رابطهٔ Z=-j/ωC محاسبه میگردد، ω=۲πf و f فرکانس و ω فرکانس زاویهای است. در برخورد با امپدانس مانند مقاومت رفتار میکنیم. .
امپدانس سلف نیز از رابطهٔ Z=jXl محاسبه میگردد که Xl=ωL و L ضریب خودالقایی سلف، و در نتیجه Z=jωL است. با توجه به ω=۲πf و رابطهٔ
Z=-j/ωC در خازن و Z=jωL در سلف نتیجه میشود که در فرکانسهای زیاد، امپدانس سلف زیاد است (سلف مانند مدار باز عمل می کند) و امپدانس خازن به سمت صفر میل میکند (خازن مانند اتصال کوتاه عمل می کند). در فرکانس های کم این موضوع برعکس می شود.
ترکیب سری
واحد امپدانس الکتریکی اهم است و میتوان با آن مانند یک مقاومت برخورد کرد. یعنی در اتصال (ترکیب) سری، امپدانسها با هم جمع می شوند؛ Z=Z۱+Z۲+Z۳+...Zn.
مثال: امپدانس کل دو امپدانس سری که اولی Z۱=۶+j۸ و دومی Z۲=۳+j۴ است برابر می شود با Z=۹+j۱۲
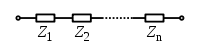
ترکیب موازی
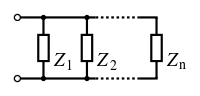
در این حالت، امپدانس کل برابر است با معکوس مجموع ادمیتانس ها (به معکوس امپدانس، ادمیتانس گفته می شود).